专题05+函数﹑基本初等函数的图像与性质(仿真押题)-2018年高考数学(理)命题猜想与仿真押题
1.已知f(x)=x+-1,f(a)=2,则f(-a)=( )
A.-4 B.-2
C.-1 D.-3
【解析】因为f(x)=x+-1,所以f(a)=a+-1=2,所以a+=3,所以f(-a)=-a--1=--1=-3-1=-4,故选A.
【答案】A
2.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
A.y= B.y=|x|-1
C.y=lgx D.y=|x|
【解析】A中函数y=不是偶函数且在(0,+∞)上单调递减,故A错误;B中函数满足题意,故B正确;C中函数不是偶函数,故C错误;D中函数不满足在(0,+∞)上单调递增,故选B.
【答案】B
3.下列四个函数:①y=3-x;②y=2x-1(x>0);③y=x2+2x-10;④y=其中定义域与值域相同的函数的个数为( )
A.1 B.2
C.3 D.4
【答案】B
4.设函数f(x)=在区间[3,4]上的最大值和最小值分别为M,m,则=( )
A. B.
C. D.
【解析】易知f(x)==2+,所以f(x)在区间[3,4]上单调递减,所以M=f(3)=2+=6,m=f(4)=2+=4,所以==.
【答案】D
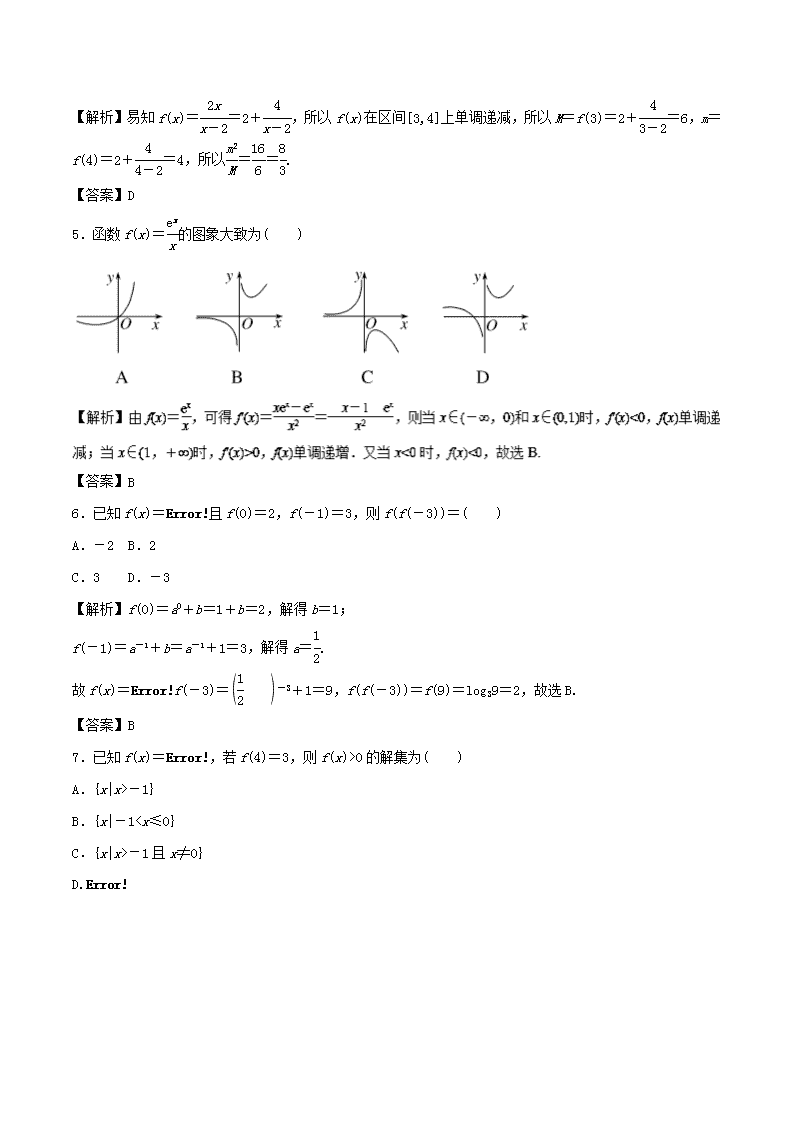
5.函数f(x)=的图象大致为( )
【答案】B
6.已知f(x)=且f(0)=2,f(-1)=3,则f(f(-3))=( )
A.-2 B.2
C.3 D.-3
【解析】f(0)=a0+b=1+b=2,解得b=1;
f(-1)=a-1+b=a-1+1=3,解得a=.
故f(x)=f(-3)=-3+1=9,f(f(-3))=f(9)=log39=2,故选B.
【答案】B
7.已知f(x)=,若f(4)=3,则f(x)>0的解集为( )
A.{x|x>-1}
B.{x|-1
-1且x≠0}
D.
【答案】D
8.定义在R上的函数f(x)对任意00的解集是( )
A.(-2,0)∪(0,2) B.(-∞,-2)∪(2,+∞)
C.(-∞,-2)∪(0,2) D.(-2,0)∪(2,+∞)
【解析】(转化法)由<1,可得<0.
令F(x)=f(x)-x,由题意知F(x)在(-∞,0),(0,+∞)上是减函数,且是奇函数,且F(2)=0,F(-2)=0,所以结合图象,令F(x)>0,得x<-2或00,a≠1)的图象如图所示,则a,b满足的关系是( )
A.01,所以0f(-),则a的取值范围是( )
A.(-∞,) B.(0,)
C.(,+∞) D.(1,)
【答案】B
12.设函数f(x)的定义域为D,如果对任意的x∈D,存在y∈D,使得f(x)=-f(y)成立,则称函数f(x)为“☆函数”.给出下列四个函数:①y=x+3;②y=x2-4x+5;③y=x3-5;④y=|2x-x2|.则其中是“☆函数”的有( )
A.1个 B.2个
C.3个 D.4个
【解析】由题意,得“☆函数”f(x)的值域关于原点对称,因为y=x+3与y=x3-5的值域都为R,所以这两个函数均为“☆函数”,而y=x2-4x+5的值域为[1,+∞),y=|2x-x2|的值域为[0,+∞),故不是“☆函数”,故选B.
【答案】B
13.函数y=lg|x|( )
A.是偶函数,在区间(-∞,0)上单调递增
B.是偶函数,在区间(-∞,0)上单调递减
C.是奇函数,在区间(0,+∞)上单调递增
D.是奇函数,在区间(0,+∞)上单调递减
【解析】因为lg|-x|=lg|x|,所以函数y=lg|x|为偶函数,又函数y=lg|x|在区间(0,+∞)上单调递增,由其图象关于y轴对称,可得y=lg|x|在区间(-∞,0)上单调递减,故选B.
【答案】B
14.函数f(x)=2|log2x|-的图象为( )
【答案】D
15.对于函数y=f(x),部分x与y的对应关系如下表:
x
1
2
3
4
5
6
7
8
9
y
3
7
5
9
6
1
8
2
4
数列{xn}满足:x1=1,且对于任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,则x1+x2+…+x2 017=( )
A.7 554 B.7 540
C.7 561 D.7 564
【解析】∵数列{xn}满足x1=1,且对任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,∴xn+1=f(xn),
∴由图表可得x2=f(x1)=3,x3=f(x2)=5,x4=f(x3)=6,x5=f(x4)=1,…,∴数列{xn
}是周期为4的周期数列,∴x1+x2+…+x2 017=504(x1+x2+x3+x4)+x1=504×15+1=7 561.故选C.
【答案】C
16.已知函数y=sin ax+b(a>0)的图象如图所示,则函数y=loga(x+b)的图象可能是( )
【解析】由题图可知00恒成立.设a=f(-4),b=f(1),c=f(3),则a,b,c的大小关系为( )
A.a0,故函数f(x)在(0,+∞)上单调递增,故f(-4)=f(4)>f(3)>f(1),即a>c>b,故选C.
【答案】C
18.下列区间中,函数f(x)=|lg(2-x)|在其上为增函数的是( )
A.(-∞,1] B.
C. D.[1,2)
【答案】D
19.已知函数f(x)=ln(1+x2),则满足不等式f(2x-1)0,-f(1)<0,则-f(1)
查看更多