数学理卷·2018届福建省厦门市湖滨中学高三上学期期中考试（2017

数学理卷·2018届福建省厦门市湖滨中学高三上学期期中考试（2017

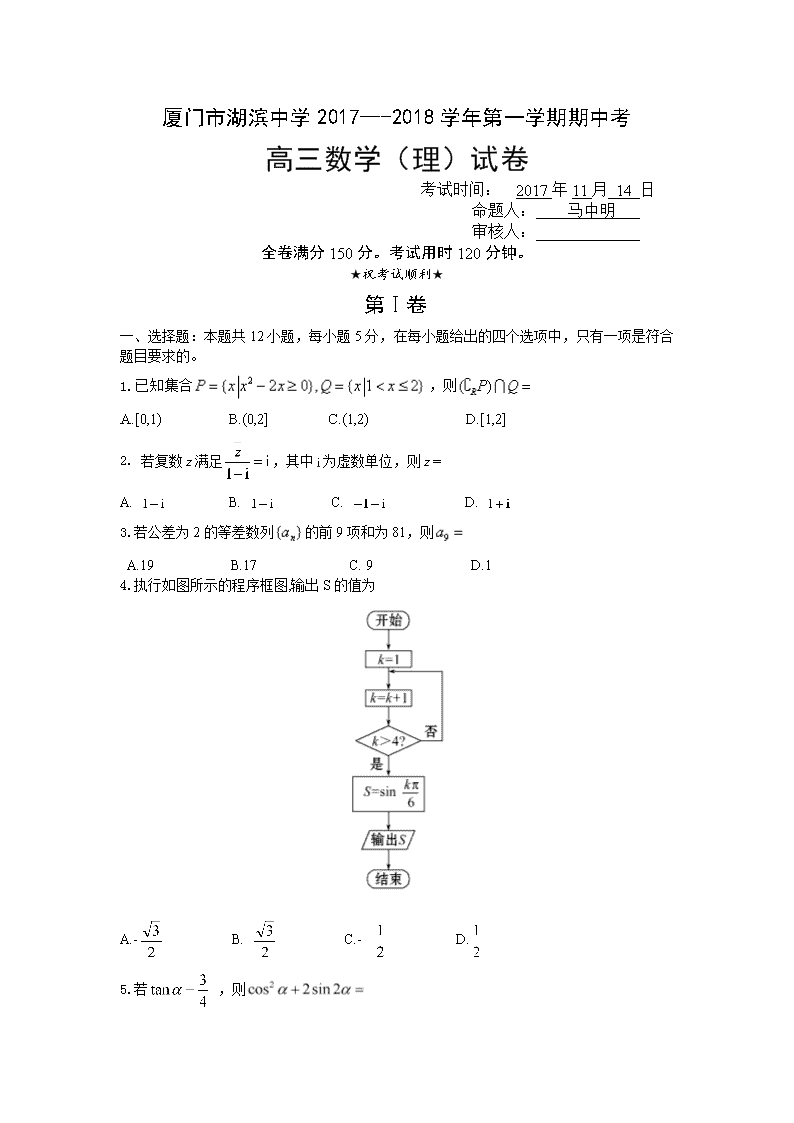
厦门市湖滨中学2017---2018学年第一学期期中考 高三数学（理）试卷 ‎ 考试时间： ‎2017年11月 14‎ 日 ‎ 命题人： 马中明 ‎ ‎ 审核人：_____________‎ 全卷满分150分。考试用时120分钟。‎ ‎★祝考试顺利★‎ 第Ⅰ卷 一、 选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。 ‎ ‎1.已知集合，则 A.[0,1)　 　B.(0,2]　 　C.(1,2)　　 D.[1,2]‎ ‎2. 若复数满足，其中为虚数单位，则=‎ A. B. C. D. ‎ ‎3.若公差为2的等差数列的前9项和为81，则 ‎ A.19 B‎.17 C. 9 D.1 ‎ ‎4.执行如图所示的程序框图,输出S的值为　‎ A.- B. C.- D.‎ ‎5.若 ，则 ‎ A. B. C. 1 D. ‎ ‎6.若函数是奇函数,则使f(x)>3成立的x的取值范围为　(　　)‎ A.(-∞,-1) B.(-1,0) C. (1,+∞) D.(0,1)‎ ‎7.已知△ABC是边长为1的等边三角形，点分别是边的中点，连接并延长到点，使得，则的值为（ ）‎ A. B. C. D.‎ ‎8.设{an}是首项为正数的等比数列，公比为q，则“q<‎0”‎是“对任意的正整数n，a2n−1+a2n<‎0”‎的（ ）‎ A.充要条件 B.充分而不必要条件 C.必要而不充分条件 D.既不充分也不必要条件 ‎9.如图，与轴的正半轴交点为，点在上，且，点在第 ‎ 一象限，，则 ‎ A. B. ‎ ‎ C. D.‎ ‎10.已知直线l过点A（﹣1，0）且与⊙B：x2+y2﹣2x=0相切于点D，以坐标轴为对称轴的双曲线E过点D，一条渐进线平行于l，则E的方程为（　　）‎ A．﹣=1 B．﹣=‎1 ‎C．﹣x2=1 D．﹣=1‎ ‎11.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体最长的棱长为（　　）‎ A．6 B． C． D．‎ ‎12.已知函数f（x）=（a>0,且a≠1）在R上单调递减，且关于x的方程恰好有两个不相等的实数解，则a的取值范围是（ ）‎ A.（0，] B.[，] C.[，]{} D.[，）{}‎ 第II卷 一、 填空题：本大题共4小题，每小题5分。‎ ‎13.已知向量，且，则 .‎ ‎14.若满足约束条件，则的最小值为 .‎ ‎15.已知为偶函数，当 时，，则曲线在点处的切线方程为______________.‎ ‎16. 已知函数f（x）=sin（ωx+）（ω＞0）在（，）上有最大值，但没有最小值，则ω的取值范围是　　．‎ 二、 解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17.（5+5=10分）设 .‎ ‎（I）求的单调递增区间；‎ ‎（II）把的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移个单位，得到函数的图象，求的值.‎ ‎18.（6+6=12分）为数列的前项和.已知,.‎ ‎（I）求的通项公式.‎ ‎（II）设,求数列的前项和.‎ ‎19.（6+6=12分） 中，角的对边分别为，.‎ ‎ （Ⅰ）求的大小；‎ ‎（Ⅱ）若，且边上的中线长为，求的值.‎ ‎20.（6+6=12分）已知数列 的前n项和Sn=3n2+8n，是等差数列，且 ‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）令 求数列的前n项和Tn.‎ ‎21.（6+6=12分）设函数，，其中 ‎（Ⅰ）求的单调区间；‎ ‎（Ⅱ）若存在极值点，且，其中，求证：；‎ ‎22.（5+7=12分）已知函数．‎ ‎（Ⅰ）讨论的单调区间；‎ ‎（Ⅱ）当时，证明：．‎ 厦门市湖滨中学2017---2018学年第一学期期中考 高三数学（理）参考答案 一． 选择题：‎ ‎1-6 CABDAD 7-12BCBDAC 二． 填空题 ‎13.8 14.2 15. 16.（，3）‎ ‎【解答】解：要求函数f（x）=sin（ωx+）（ω＞0）在（，）上有最大值，但没有最小值，‎ ‎∴ω•+＜＜ω•+≤‎ 解之即可得：ω∈（，3）．‎ 故答案为（，3）．‎ 三．解答题 ‎17.‎ 由得 所以，的单调递增区间是 ‎ （或）‎ ‎18.解析：(1)由+2an=4Sn+3,可知+2an+1=4Sn+1+3,‎ 可得-+2(an+1-an)=4an+1,即2(an+1+an)=-=(an+1+an)(an+1-an),‎ 由于an>0,可得an+1-an=2,又+‎2a1=‎4a1+3,解得a1=-1(舍去),a1=3.‎ 所以{an}是首项为3,公差为2的等差数列,通项公式为an=2n+1.‎ ‎(2)由an=2n+1可知 设数列{bn}的前n项和为Tn,则 ‎19.‎ ‎20.试题解析：（Ⅰ）由题意知当时，，‎ 当时，，‎ 所以.‎ 设数列的公差为，‎ 由，即，可解得，‎ 所以.‎ ‎（Ⅱ）由（Ⅰ）知，‎ 又，‎ 得，‎ ‎，‎ 两式作差，得所以 ‎21.试题解析：（1）解：由，可得，下面分两种情况讨论：‎ ①当时，有恒成立，所以的单调增区间为.‎ ②当时，令，解得或.‎ 当变化时，、的变化情况如下表：‎ ‎0‎ 单调递增 极大值 单调递减 极小值 单调递增 所以的单调递减区间为，单调递增区间为，.‎ ‎（2）证明：因为存在极值点，所以由（1）知且.‎ 由题意得，即，‎ 进而，‎ 又，且，‎ 由题意及（1）知，存在唯一实数满足，学科&网且，因此，‎ 所以.‎ ‎22.‎ ‎（Ⅱ）证明：要证men+n＜nem+m，即证men﹣m＜nem﹣n，‎ 也就是证m（en﹣1）＜n（em﹣1）．也就是证＜，‎ 令g（x）=，x＞0，g′（x）=，‎ 再令h（x）=xex﹣ex+1，h′（x）=ex+xex﹣ex=xex＞0，‎ 可得h（x）在x＞0递增，即有h（x）＞h（0）=0，‎ 则g′（x）＞0，g（x）在（0，+∞）递增，‎ 由m＞n＞0，可得＜，‎ 故原不等式成立．‎