- 2021-06-19 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届山西省高三省际名校联考(三)(2018
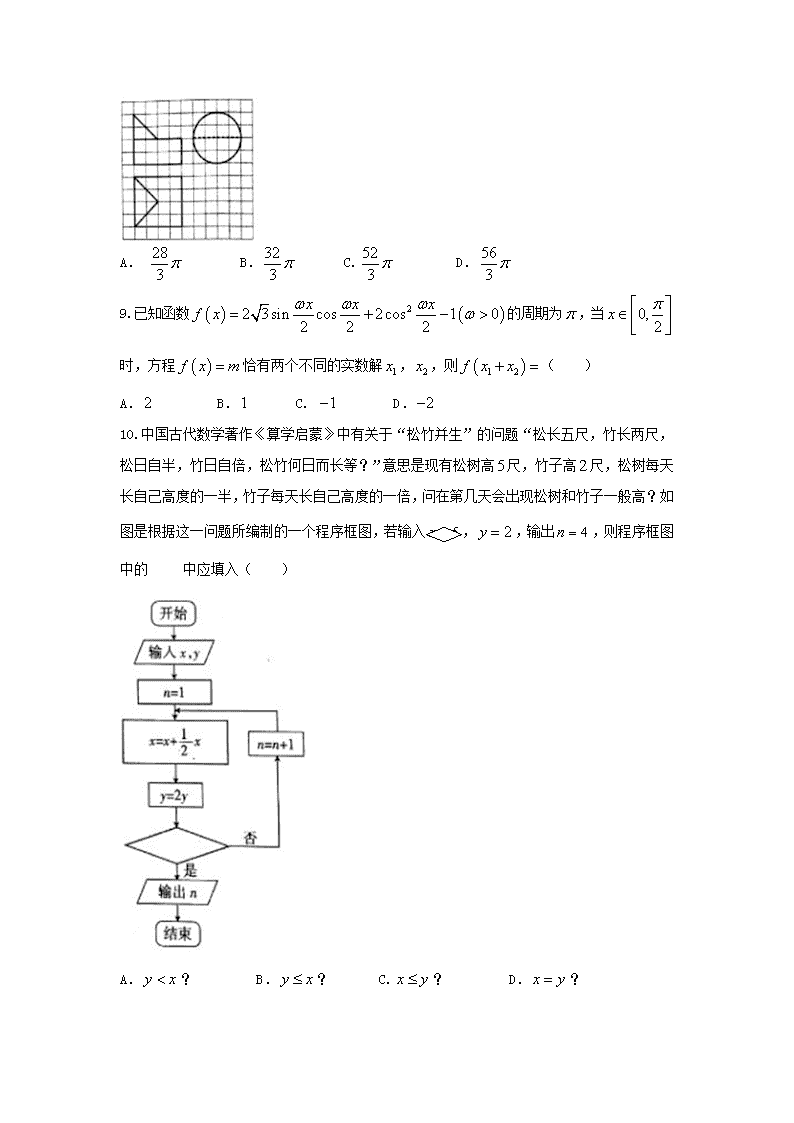
2018届山西省高三省际名校联考(三) 文科数学 第Ⅰ卷(共60分) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,,全集,则( ) A. B. C. D. 2.已知平面向量,,则向量的模是( ) A. B. C. D. 3.“”是“”的( ) A.充分不必要条件 B.必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 4.问题“今有女子不善织布,逐日所织的布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?”源自南北朝张邱建所著的《张邱建算经》,该问题的答案是( ) A.尺 B.尺 C. 尺 D.尺 5.若函数为奇函数,则( ) A. B. C. D. 6.从装有大小材质完全相同的个红球和个黑球的不透明口袋中,随机摸出两个小球,则两个小球同色的概率是( ) A. B. C. D. 7.已知为直线上的点,过点作圆的切线,切点为,,若,则这样的点有( ) A.个 B.个 C. 个 D.无数个 8.某几何体的三视图如图所示,若图中小正方形的边长均为,则该几何体的体积是( ) A. B. C. D. 9.已知函数的周期为,当时,方程恰有两个不同的实数解,,则( ) A. B. C. D. 10.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等?”意思是现有松树高尺,竹子高尺,松树每天长自己高度的一半,竹子每天长自己高度的一倍,问在第几天会出现松树和竹子一般高?如图是根据这一问题所编制的一个程序框图,若输入,,输出,则程序框图中的 中应填入( ) A.? B.? C.? D.? 11.已知函数,若曲线上存在点使得,则实数的取值范围是( ) A. B. C. D. 12.在四面体中,,,底面,的面积是,若该四面体的顶点均在球的表面上,则球的表面积是( ) A. B. C. D. 第Ⅱ卷(共90分) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.复数满足,则复数的共轭复数 . 14.已知实数,满足约束条件则的最大值是 . 15.是为双曲线上的点,,分别为的左、右焦点,且,与轴交于点,为坐标原点,若四边形有内切圆,则的离心率为 . 16.数列满足若,则数列的前项的和是 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 在中,内角,,的对边分别为,,,且. (1)求; (2)若,且的面积为,求的周长. 18. 如图,三棱柱中,,平面. (1)证明:平面平面; (2)若,,求点到平面的距离. 19. 某大型商场去年国庆期间累计生成万张购物单,从中随机抽出张,对每单消费金额进行统计得到下表: 消费金额(单位:元) 购物单张数 25 25 30 10 10 由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题: (1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过元的概率; (2)为鼓励顾客消费,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值元、元、元的奖品.已知中奖率为,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为.若今年国庆期间该商场的购物单数量比去年同期增长,式预测商场今年国庆期间采办奖品的开销. 20. 已知抛物线的焦点为,为轴上的点. (1)过点作直线与相切,求切线的方程; (2)如果存在过点的直线与抛物线交于,两点,且直线与的倾斜角互补,求实数的取值范围. 21. 已知函数. (1)讨论函数的单调性; (2)当时,曲线总在曲线的下方,求实数的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程 在平面直角坐标系中,以原点为极点,轴的非负半轴为极轴建立极坐标系.已知曲线的极坐标方程为,为曲线上的动点,与轴、轴的正半轴分别交于,两点. (1)求线段中点的轨迹的参数方程; (2)若是(1)中点的轨迹上的动点,求面积的最大值. 23.选修4-5:不等式选讲 已知函数. (1)解不等式; (2)若关于的不等式只有一个正整数解,求实数的取值范围. 试卷答案 一、选择题 1-5: ACBAD 6-10: CBABC 11、12:BD 二、填空题 13. 14. 15. 16. 三、解答题 17.解:(1)∵,∴. ∴, ∴. ∵,∴,∴,∴. (2)∵的面积为,∴,∴. 由,及,得,∴. 又,∴. 故其周长为. 18.(1)证明:∵平面,∴. ∵, ∴,∴平面. 又平面,∴平面平面. (2)解法一:取的中点,连接. ∵,∴. 又平面平面,且交线为, 则平面. ∵平面,∴, ∴四边形为菱形,∴. 又,∴是边长为正三角形,∴. ∴. 设点到平面的距离为. 则. 又,∴. 所以点到平面的距离为. 解法二:利用平面转化为求点到平面的距离,即. 19. 解:(1)因消费在区间的频率为,故中位数估计值即为. 设所求概率为,而消费在的概率为. 故消费在区间内的概率为. 因此消费额的平均值可估计为. 令其与中位数相等,解得. (2)设等比数列公比为,根据题意, 即,解得. 故一等奖、二等奖、三等奖的中奖率分别为,,. 今年的购物单总数约为. 其中具有抽奖资格的单数为, 故一等奖、二等奖、三等奖中奖单数可估计为,,. 于是,采购奖品的开销可估计为(元). 20. 解:(1)设切点为,则. ∴点处的切线方程为. ∵过点,∴,解得或. 当时,切线的方程为, 当时,切线的方程为或. (2)设直线的方程为,代入得. 设,,则,. 由已知得, 即,∴. 把①代入②得,③ 当时,显然成立, 当时,方程③有解,∴,解得,且. 综上,. 21.解:(1)由可得的定义域为,且, 若,则,函数在上单调递增; 若,则当时,,在上单调递增, 当时,,在上单调递减. 综上,当时,函数在上单调递增; 当时,在上单调递增,在上单调递减. (2)解法一:原命题等价于不等式在上恒成立, 即证在上恒成立, 令,则,, 设, (i)当时,在上单调递增, 又∵, ∴当时,恒成立,即恒成立. ∴,与题意不符,舍去. (ii)当时,若在上恒成立, 只需在上单调递减,即在上恒成立. 又∵在上单调递减, ∴,即. 解法二:原命题等价于不等式在上恒成立, 即,不等式恒成立. ∵当时,,∴, 即证当时,大于的最大值. 又∵当时,,∴, 综上所述,. 22. 解:(1)由的方程可得,又,, ∴的直角坐标方程为,即. 设,则, ∴点的轨迹的参数方程为(为参数). (2)由(1)知点的轨迹的普通方程为,,,,所以直线的方程为. 设,则点到的距离为 , ∴面积的最大值为. 23.解: (1)当时,,解得,∴; 当时,,解得,∴; 当时,,解得,∴. 综上,不等式的解集为. (2)作出函数与的图象,由图象可知当时, 不等式只有一个正整数解, ∴.查看更多