2017-2018学年河北省定州市第二中学高二上学期第一次月考数学（文）试题

2017-2018学年河北省定州市第二中学高二上学期第一次月考数学（文）试题

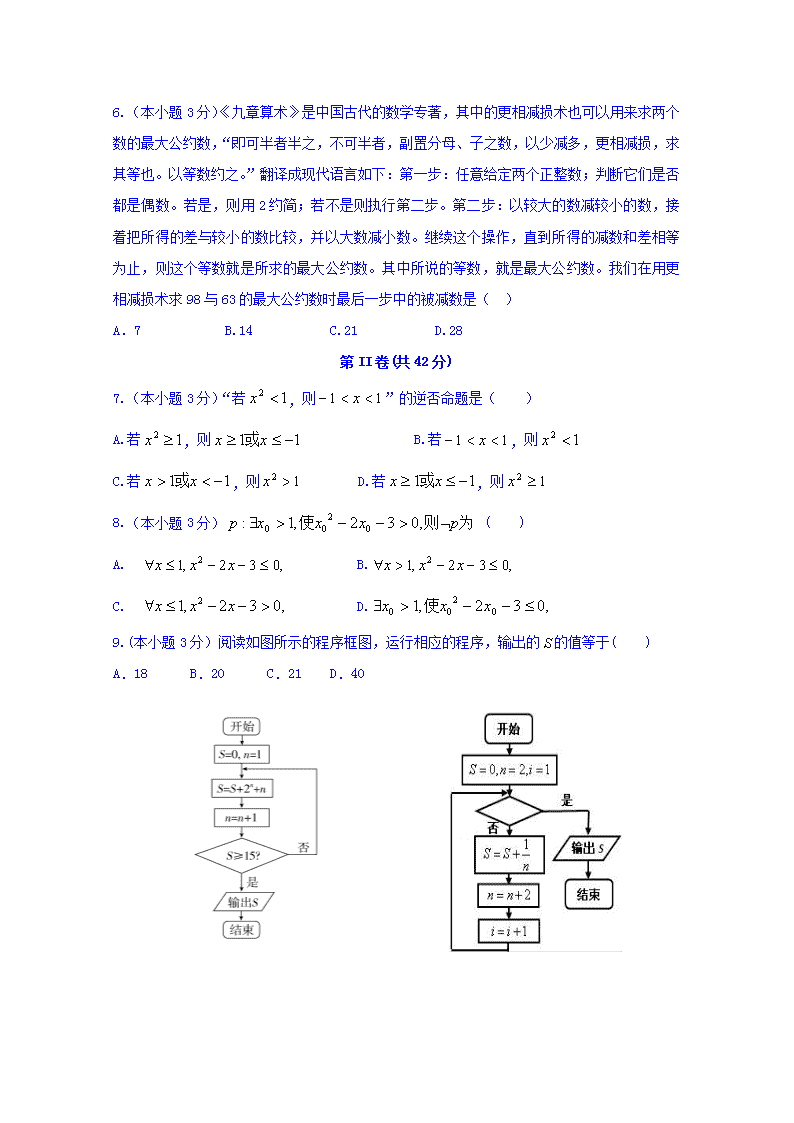
定州二中2017--2018年度第一学期第一次月考 数学学科高二文科试题 总分：120分 考试时间：90分钟 第I卷（共18分）‎ ‎1.（本小题3分）某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如下 ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎　‎ 甲 ‎　‎ 乙 ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎8‎ ‎0‎ ‎4‎ ‎6‎ ‎3‎ ‎1‎ ‎2‎ ‎5‎ ‎3‎ ‎6‎ ‎8‎ ‎2‎ ‎5‎ ‎4‎ ‎3‎ ‎8‎ ‎9‎ ‎3‎ ‎1‎ ‎6‎ ‎1‎ ‎6‎ ‎7‎ ‎9‎ ‎4‎ ‎4‎ ‎9‎ ‎1‎ ‎5‎ ‎0‎ 据此分析，甲、乙两位运动员得分的中位数分别为（ ）‎ A.23,36B.26,31C.26,36D.28,37‎ ‎2.（本小题3分)一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是（ ）‎ A.至多有一次中靶 B.两次都中靶 C.只有一次中靶D.两次都不中靶 ‎3.（本小题3分）某种饮料每箱装6听，其中2听不合格，问质检人员从中随机抽出2听，则检出不合格的概率为（ ）‎ A.B. C. D.‎ ‎4.（本小题3分）下列命题中真命题的个数为（ ）‎ ‎（1）若，则方程有实数根的逆命题；‎ ‎（2）条件是条件的必要条件；‎ ‎（3）的否定.‎ A.0 B.1 C.2 D.3 ‎ ‎5.（本小题3分）在圆上任取一点，过点作轴的垂线段，为垂足，当点在圆上运动时，线段的中点的轨迹方程为（ ）‎ A. B. C. D.‎ ‎6.（本小题3分）《九章算术》是中国古代的数学专著，其中的更相减损术也可以用来求两个数的最大公约数，“即可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。”翻译成现代语言如下：第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止，则这个等数就是所求的最大公约数。其中所说的等数，就是最大公约数。我们在用更相减损术求98与63的最大公约数时最后一步中的被减数是（ ）‎ A．7 B.14 C.21 D.28 ‎ 第II卷(共42分)‎ ‎7.（本小题3分）“若，则”的逆否命题是（ ）‎ A.若，则 B.若，则 C.若，则 D.若，则 ‎8.（本小题3分） ( )‎ A. B.‎ C. D.‎ ‎9.(本小题3分）阅读如图所示的程序框图，运行相应的程序，输出的的值等于(　　)‎ A．18 B．20 C．21 D．40‎ ‎（9题图）（10题图）‎ ‎10.(本小题3分）给出计算的值的一个程序框图如图，其中判断框内应填入的条件是（　　）‎ A.i＞10 B．i＜10 C．i＞20 D．i＜20‎ ‎11.(本小题5分）学校为了解学生学习数学的情况，采用分层抽样的方法从高一600人，高二780人，高三人中，抽取35人进行问卷调查，已知高二被抽去的人数为13人，则=．‎ ‎12.（本小题5分）将参加夏令营的600名学生编号为：001，002，…，600.采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003，这600名学生分住在三个营区．从001到300在第Ⅰ营区，从301到495在第Ⅱ营区，从496到600在第Ⅲ营区．第二个营区被抽中的人数为．‎ ‎13.（本小题5分）从某班5位老师中随机选两位老师值班，有女老师被选中的概率为，则在这5位老师中，女老师有人.‎ ‎14.（本小题4分）为轴上一点，是椭圆的两个焦点，为正三角形，且的中点恰好在椭圆上，则椭圆的离心率为．‎ ‎15.（本小题5分）在平面坐标系中，的顶点，顶点在椭圆上，则．‎ ‎16.（本小题5分）已知是三角形所在平面内一点，，现将一粒黄豆撒在内，则黄豆落在内的概率为．‎ 第卷（共60分）‎ ‎17.（本小题12分）‎ 已知命题，命题，若命题是真命题，求实数的取值范围。‎ ‎18.（本小题12分）我国是世界上严重缺水的国家,某市政府为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如下的频率分布直方图.‎ ‎(1)求直方图中的a值.‎ ‎(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.‎ ‎(3)估计居民月均用水量的中位数.‎ ‎19.（本小题12分）已知椭圆分别为椭圆的左右焦点，为椭圆的上顶点，直线与椭圆交于另一点.‎ (1) 若，求椭圆的离心率；‎ (2) 若椭圆的焦距为2，且，求椭圆的方程.‎ ‎20.（本小题12分）据2013年12月23日新华社电中央办公厅印发《关于培育和践行社会主义核心价值观的意见》，将24字核心价值观分成3个层面：国家层面：富强民主文明和谐；社会层面：自由平等公正法治；公民层面：爱国敬业诚信友善共计12个关键词。‎ （1） 从这12个词中随机选1个，求这个关键词属于国家层面的概率；‎ （2） 在社会层面和公民层面的关键词中各选1个，求选中“平等”和未选中“敬业”的概率；‎ （3） 从这12个关键词中任选2个，求这2个关键词不属于同一个层面的概率。‎ ‎21.（本小题12分）下表是定州二中从2013年到2017年，高考本一上线人数在参加高考的学生总人数中的比重：‎ 年份 ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ 年份代码 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 本一上线人数比重/%‎ ‎44.3‎ ‎45.5‎ ‎46.9‎ ‎48.1‎ ‎50.5‎ 根据表中信息回答下列问题：‎ （1） 通过分析得知本一上线人数比重与年份代码具有线性相关关系，求关于的回归方程；‎ （2） 已知该校2016级在校生为3000人，按照当前的变化趋势，预测2019年该校本一上线人数（保留到整数）.‎ 附：回归直线的斜率和截距：，.‎ 高二数学文科参考答案 ‎1-5 CDDBC 6-10 BDBBA ‎11、720 12、17 13、2 14、 15、 16、‎ ‎17、解：若真则；若真则；因为是真命题所以或 ‎18、解：(1)由概率统计相关知识,各组频率之和的值为1,因为频率=(频率/组距)×组距,所以0.5×(0.08+0.16+0.42+0.5+0.12+0.08+0.04+2a)=1,得a=0.3.‎ ‎(2)由图可知,全市居民中月均用水量不低于3吨的人数所占百分比为0.5×(0.12+0.08+0.04)=12%,所以全市月均用水量不低于3吨的人数为:30×12%=3.6(万).‎ ‎(3)设中位数为x吨,因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5,由0.5×=0.5-0.48,解得x=2.04,故可估计居民月均用水量的中位数为2.04吨.‎ ‎19、（1） (2)‎ ‎20、（1）；（2）；（3）‎ ‎21、（1）回归直线方程为；（2）2019年的年份代码为7代入回归直线方程可得，所以本一上线人数为