2019届二轮复习小题满分限时练(六)作业(全国通用)
限时练(六)
(限时:45分钟)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合P={x|y=},Q={x|ln x<1},则P∩Q=( )
A.(0,2] B.[-2,e) C.(0,1] D.(1,e)
解析 由-x2-x+2≥0,得-2≤x≤1,则P=[-2,1],又Q={x|0
1,b=log0.40.5∈(0,1),c=log80.4<0,∴a>b>c.
答案 B
4.设函数f(x)=x2-2x-3,若从区间[-2,4]上任取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
A. B. C. D.
解析 由f(x0)≤0,得到x-2x0-3≤0,
且x0∈[-2,4],解得-1≤x0≤3,
故所求事件概率p==.
答案 A
5.在一次化学测试中,高一某班50名学生成绩的平均分为82分,方差为8.2,则下列四个数中不可能是该班化学成绩的是( )
A.60 B.70 C.80 D.100
解析 ∵ (xi-82)2=8.2,(60-82)2=9.68.
∴8.2<9.68,因此化学成绩不可能为60.
答案 A
6.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若c=3,a=6sin A,△ABC的面积S=,则a+b=( )
A. B. C. D.5
解析 在△ABC中,c=3,a=6sin A,
∴==,则sin C=,C=.
又S=absin=,知ab=4.
由余弦定理,32=a2+b2-2abcos=(a+b)2-3ab.
∴(a+b)2=9+3ab=21,故a+b=.
答案 A
7.执行如图所示的程序框图,输出的s值为( )
A.2 B. C. D.
解析 k=0,s=1,满足k<3,循环;k=1,s=2,满足k<3,再循环;k=2,s=,满足k<3,再循环;k=3,s==,不满足k<3,输出s=.
答案 C
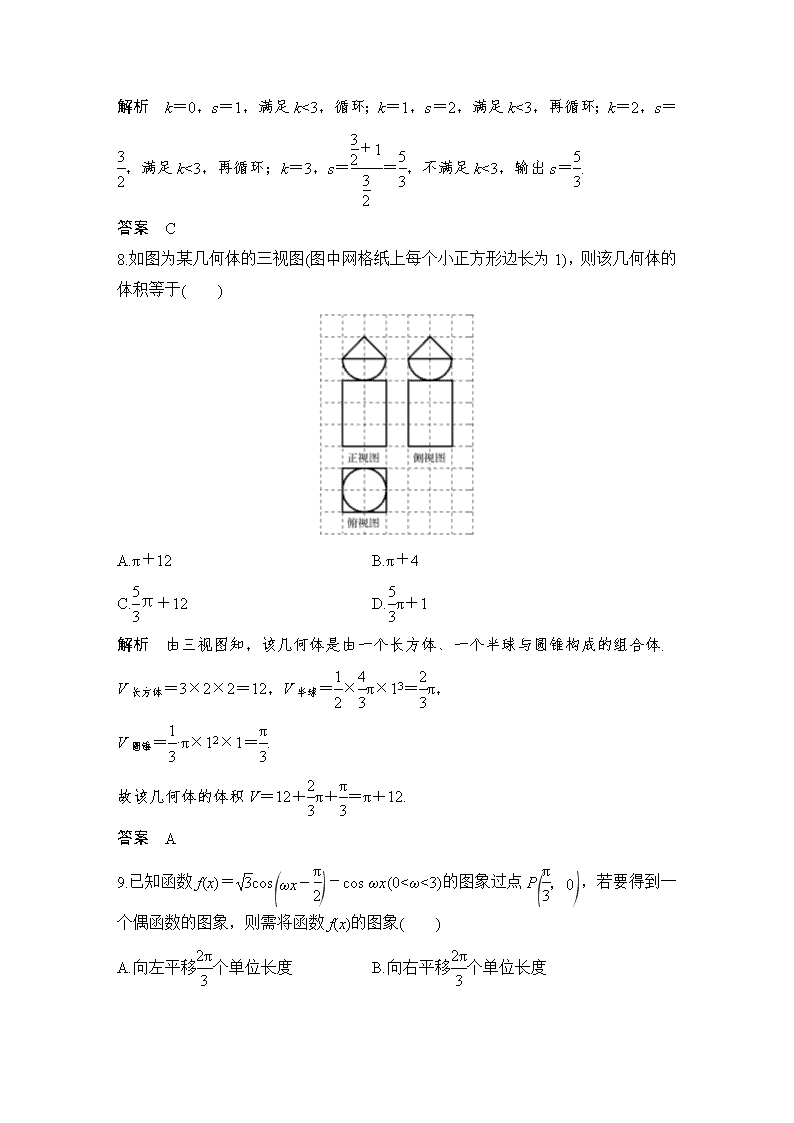
8.如图为某几何体的三视图(图中网格纸上每个小正方形边长为1),则该几何体的体积等于( )
A.π+12 B.π+4
C.π+12 D.π+1
解析 由三视图知,该几何体是由一个长方体、一个半球与圆锥构成的组合体.
V长方体=3×2×2=12,V半球=×π×13=π,
V圆锥=·π×12×1=.
故该几何体的体积V=12+π+=π+12.
答案 A
9.已知函数f(x)=cos-cos ωx(0<ω<3)的图象过点P,若要得到一个偶函数的图象,则需将函数f(x)的图象( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
解析 f(x)=sinωx-cos ωx=2sin,又P在函数f(x)的图象上,
∴ω-=kπ(k∈Z),ω=3k+,又0<ω<3,∴ω=,f(x)=2sin.当将f(x)图象向右平移个单位,得y=2sin的图象,即y=2sin=
-2cos x为偶函数.
答案 B
10.已知数列{an}为等差数列,且a1≥1,a2≤5,a5≥8,设数列{an}的前n项和为Sn,S15的最大值为M,最小值为m,则M+m=( )
A.500 B.600 C.700 D.800
解析 由题意,可知公差最大值时,S15最大;公差最小时,S15最小.可得a1=1,a2=5,此时公差d=4是最大值,M=S15=1×15+×4=435.
当a2=5,a5=8,此时d=1是最小值,a1=4,
m=S15=4×15+×1=165.
M+m=435+165=600.
答案 B
11.若双曲线C:-=1(a>0,b>0)的中心为O,过C的右顶点和右焦点分别作垂直于x轴的直线,交C的渐近线于A,B和M,N,若△OAB与△OMN的面积比为1∶4,则C的渐近线方程为( )
A.y=±x B.y=±x
C.y=±2x D.y=±3x
解析 依题可知△AOB与△MON相似,由三角形面积比等于相似比的平方,
得=,
所以=2,即=4,所以=,
所以C的渐近线方程为y=±x.
答案 B
12.已知函数f(x)=的图象上关于y轴对称的点至少有3对,则实数a的取值范围是( )
A. B.
C. D.
解析 f(x)=
令φ(x)=sin-1(x<0),则φ(x)关于y轴对称的函数为g(x)=-sin-1(x>0),
则函数f(x)的图象上关于y轴对称的点至少有3对,即函数g(x)的图象与函数h(x)=logax(a>0,a≠1)的图象至少有3个交点(如图所示),则0
查看更多