2018-2019学年湖北省宜昌市葛洲坝中学高二5月月考数学（文）试题 Word版

2018-2019学年湖北省宜昌市葛洲坝中学高二5月月考数学（文）试题 Word版

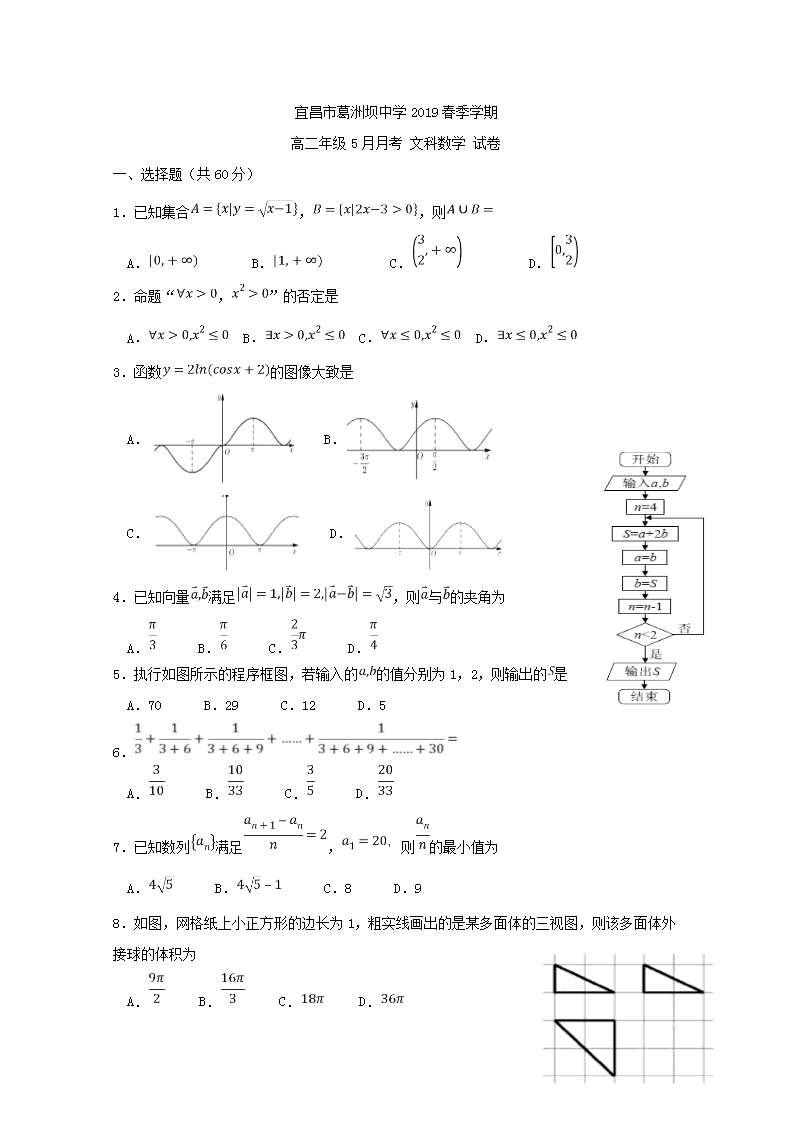
宜昌市葛洲坝中学2019春季学期 高二年级5月月考 文科数学 试卷 一、选择题（共60分）‎ ‎1．已知集合，，则 A． B． C． D．‎ ‎2．命题“，”的否定是 ‎ A． B． C． D．‎ ‎3．函数的图像大致是 ‎ A． B．‎ C． D．‎ ‎4．已知向量满足，则与的夹角为 A． B． C． D．‎ ‎5．执行如图所示的程序框图，若输入的的值分别为1，2，则输出的是 ‎ A．70 B．29 C．12 D．5‎ ‎6．‎ A． B． C． D．‎ ‎7．已知数列满足，则的最小值为 A． B． C．8 D．9‎ ‎8．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体外接球的体积为 ‎ A． B． C． D．‎ ‎9．已知函数在上单调递增，则实数的取值范围是 ‎ A． B． C． D．或 10. 已知函数是定义在上的奇函数，对任意的都有，‎ 当时，，则 ‎ A． B． C． D．‎ ‎11．已知点在圆上，点在抛物线上，则的最小值为 ‎ A．1 B．2 C．3 D．4‎ 12. 设函数在上存在导函数，对于任意的实数，都有，当 时，，若，则实数的取值范围是 A． B． C． D．‎ 二、填空题（共20分）‎ ‎13．若（为虚数单位）是纯虚数，则实数_________.‎ ‎14．在区间和内分别取一个数，记为a和b，则方程表示离心率小于的双曲线的概率为________．‎ ‎15．已知函数对于任意实数都有，且当时，，若实数满足，则的取值范围是________．‎ ‎16．我国齐梁时代的数学家祖暅提出了一条原理：“幂势既同，则积不容异”.意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图，将底面直径都为，高皆为的椭半球体和已被挖去了圆锥体的圆柱放置于同一平面上，用平行于平面且与平面任意距离处的平面截这两个几何体，可横截得到及两截面.可以证明总成立.据此，半短轴长为1，半长轴长为3的椭球体的体积是_______．‎ 三、解答题（共70分）‎ ‎17（12分）．的内角所对的边分别是，且，.‎ ‎（1）求；‎ ‎（2）若边上的中线，求的面积.‎ ‎18（12分）．已知四棱锥，，，平面，，，直线与平面所成角的大小为，是线段的中点.‎ ‎（1）求证：平面；‎ ‎（2）求点到平面的距离.‎ ‎19（12分）．2018年，依托用户碎片化时间的娱乐需求、分享需求以及视频态的信息负载力，短视频快速崛起；与此同时，移动阅读方兴未艾，从侧面反应了人们对精神富足的一种追求，在习惯了大众娱乐所带来的短暂愉悦后，部分用户依旧对有着传统文学底蕴的严肃阅读青睐有加．‎ 某读书APP抽样调查了非一线城市M和一线城市N各100名用户的日使用时长（单位：分钟），绘制成频率分布直方图如下，其中日使用时长不低于60分钟的用户记为“活跃用户”．‎ ‎（1）请填写以下列联表，并判断是否有99．5%的把握认为用户活跃与否与所在城市有关？‎ 活跃用户 不活跃用户 合计 城市M 城市N 合计 ‎（2）该读书APP还统计了2018年4个季度的用户使用时长y（单位：百万小时），发现y与季度（）线性相关，得到回归直线为，已知这4个季度的用户平均使用时长为12.3百万小时，试以此回归方程估计2019年第一季度（）该读书APP用户使用时长约为多少百万小时．‎ 附：，其中．‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎20（12分）．已知椭圆的左、右焦点分别为（）．点在上，，△的周长为，面积为． ‎ ‎（1）求的方程；‎ ‎（2）过的直线与交于两点，以为直径的圆与直线相切，求直线的方程．‎ ‎21（12分）．已知函数．‎ ‎(Ⅰ)求函数的极值；‎ ‎(Ⅱ)若,且,求证：．‎ ‎22（10分）．在平面直角坐标中，直线的参数方程为（为参数，为常数）．以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．‎ ‎（Ⅰ）求直线的普通方程和曲线的直角坐标方程；‎ ‎（Ⅱ）设直线与曲线相交于两点，若，求的值．‎ 参考答案 ‎1．B 2．B 3．C 4．A 5．B 6．D 7．C 8．A 9．C 10．A 11．A 12．A ‎13． 14． 15． 16．‎ ‎17．（1），（2）‎ ‎（1）由正弦定理得，‎ 所以，‎ 因为，所以，‎ 即，所以，‎ 又因为，所以，.‎ ‎（2）在和中，由余弦定理得 ‎，.‎ 因为，，，，‎ 又因为，即，‎ 所以，‎ 所以，‎ 又因为，所以.‎ 所以的面积.‎ ‎18．（1）见证明；（2）‎ ‎（1）因为平面，平面，所以，‎ 因为，是线段的中点，所以，‎ 又，平面，平面， 所以平面，‎ 又平面，所以.‎ 取上点，使得，连接，所以且，‎ 所以四边形为平行四边形，所以，‎ 所以直线与平面所成角的大小等于直线与平面所成角的大小，‎ 又平面，，所以平面，‎ 所以为直线与平面所成的角，‎ 所以，所以，‎ 因为，，所以，‎ 所以，，，‎ 所以，，‎ 所以，所以，‎ 因为，平面，‎ 所以平面.‎ ‎（2）由（1）可知平面，所以和均为直角三角形，‎ 又，设点到平面的距离为，‎ 则，即，‎ 化简得，解得，‎ 所以点到平面的距离为.‎ ‎19．(1)见解析；(2)见解析；(3) 百万小时 ‎（1）由已知可得以下列联表：‎ 活跃用户 不活跃用户 合计 城市M ‎60‎ ‎40‎ ‎100‎ 城市N ‎80‎ ‎20‎ ‎100‎ 合计 ‎140‎ ‎60‎ ‎200‎ 计算 ，‎ 所以有99．5%的把握认为用户是否活跃与所在城市有关． ‎ ‎（2）由已知可得，又，‎ 可得，所以，所以． ‎ 以代入可得（百万小时），‎ 即2019年第一季度该读书APP用户使用时长约为百万小时．‎ ‎20．（1）（2）‎ ‎（1）设椭圆，‎ 依题意知△的周长为，得，…① ‎ 又因为，所以， ‎ 所以△的面积，‎ 所以，即…②， ‎ 联立①②解得，则， ‎ 所以的方程为．‎ ‎（2）当直线斜率为0时，不满足题意．‎ 设直线的方程为，，‎ 由消去，得， ‎ 从而， ‎ 所以 ‎ ， ‎ ‎ 设以为直径的圆的圆心，半径为，则，‎ 又，, ‎ 又因为圆与直线相切，则，即，解得．‎ 所以直线的方程为，即 ‎21．(Ⅰ)极大值为：，无极小值；(Ⅱ)见解析.‎ ‎(Ⅰ) 的定义域为且 令，得；令，得 在上单调递增，在上单调递减 函数的极大值为，无极小值 ‎(Ⅱ)， ，即 由(Ⅰ)知在上单调递增，在上单调递减 且，则 要证，即证，即证，即证即证 由于，即，即证 令 则 ‎ 恒成立 在递增 在恒成立 ‎ ‎22．（Ⅰ），（Ⅱ）‎ ‎（Ⅰ）∵直线的参数方程为（为参数，为常数），‎ 消去参数得的普通方程为：即． ‎ ‎∵，∴即，即．‎ 故曲线的直角坐标方程为．‎ ‎（Ⅱ）法一：将直线的参数方程代入曲线中得，‎ ‎∴．‎ 法二：将代入曲线 化简得：,‎ ‎∴．‎