【推荐】专题8-5+直线、平面垂直的判定和性质-2018年高三数学（文）一轮总复习名师伴学

【推荐】专题8-5+直线、平面垂直的判定和性质-2018年高三数学（文）一轮总复习名师伴学

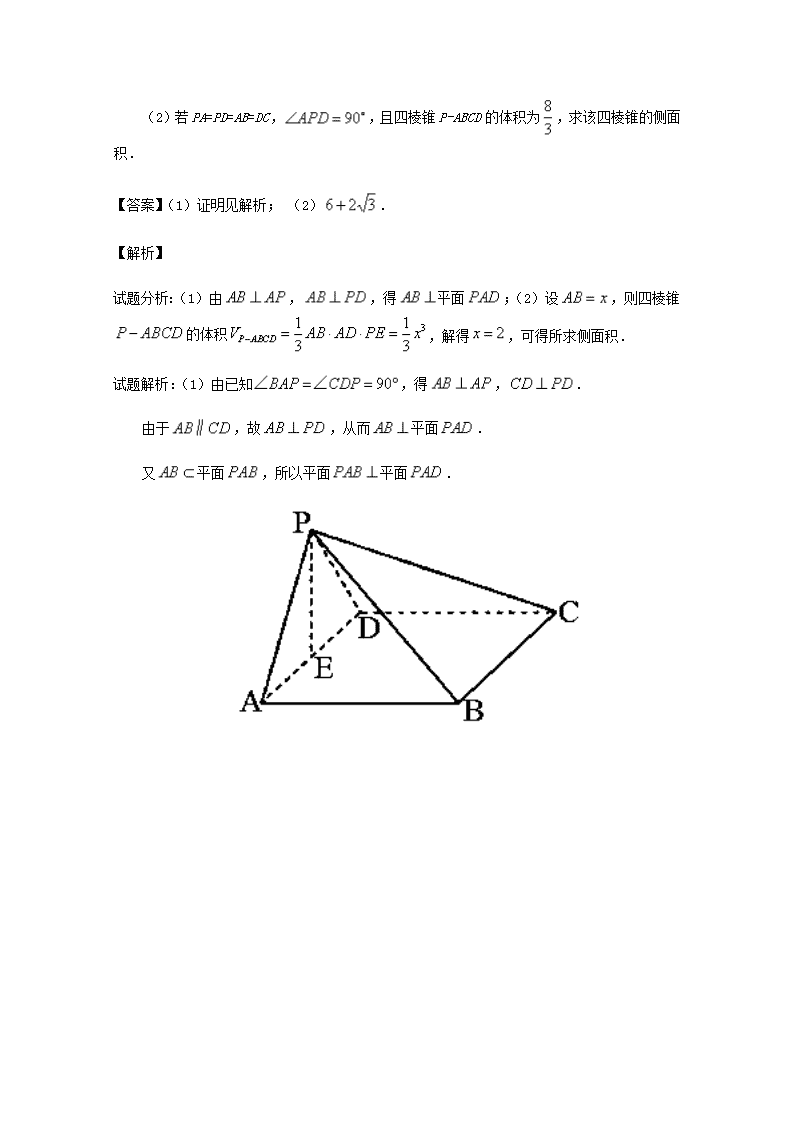
‎1.【2017课标3，文10】在正方体中，E为棱CD的中点，则（ ）‎ A． B． C． D． ‎【答案】C ‎【考点】线线位置关系 ‎【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.‎ ‎(1)证明线面、面面平行，需转化为证明线线平行.‎ ‎(2)证明线面垂直，需转化为证明线线垂直.‎ ‎(3)证明线线垂直，需转化为证明线面垂直.‎ ‎2.【2017课标1，文18】如图，在四棱锥P-ABCD中，AB//CD，且．‎ ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC，，且四棱锥P-ABCD的体积为，求该四棱锥的侧面积．‎ ‎【答案】（1）证明见解析； （2）．‎ ‎【解析】‎ 试题分析：（1）由，，得平面；（2）设，则四棱锥的体积，解得，可得所求侧面积． ‎ 试题解析：（1）由已知，得，．‎ 由于，故，从而平面．‎ 又平面，所以平面平面．‎ ‎【考点】空间位置关系证明，空间几何体体积、侧（表）面积计算 ‎【名师点睛】证明面面垂直，先由线线垂直证明线面垂直，再由线面垂直证明面面垂直；先利用线面平行说明点面距为定值，计算点面距时，如直接求不方便，应首先想到转化，如平行转化、对称转化、比例转化等，找到方便求值时再计算，可以减少运算量，提高准确度，求点到平面的距离有时能直接作出就直接求出，不方便直接求出的看成三棱锥的高，利用等体积法求出．‎ ‎3.【2017江苏，15】 如图,在三棱锥A-BCD中,AB⊥AD, BC⊥BD, 平面ABD⊥平面BCD, 点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.‎ ‎ 求证： AD⊥AC.‎ ‎【答案】见解析 ‎【考点】线面垂直判定与性质定理，面面垂直性质定理 ‎【名师点睛】‎ ‎(1)证明线面垂直，需转化为证明线线垂直.‎ ‎(2)证明线线垂直，需转化为证明线面垂直.‎ ‎4.【2016高考北京文数】如图，在四棱锥中，平面， ‎（I）求证：；‎ ‎（II）求证：；‎ ‎（III）设点E为AB的中点，在棱PB上是否存在点F，使得平面?说明理由.‎ ‎【答案】（Ⅰ）见解析；（Ⅱ）见解析；（III）存在.理由见解析.‎ ‎（II）因为，，‎ 所以．‎ 因为平面，‎ 所以．‎ 所以平面．‎ 所以平面平面．‎ ‎（III）棱上存在点，使得平面．证明如下：‎ 取中点，连结，，．‎ 又因为为的中点，‎ 所以．‎ 又因为平面，‎ 所以平面．‎ ‎ ‎ 考点：空间垂直判定与性质；空间想象能力，推理论证能力 ‎【名师点睛】平面与平面垂直的性质的应用：当两个平面垂直时，常作的辅助线是在其中一个面内作交线的垂线，把面面垂直转化为线面垂直，进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系)，构造(寻找)二面角的平面角或得到点到面的距离等. ‎ ‎5. 【2016高考江苏卷】如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且 ，.‎ 求证：平面B1DE⊥平面A1C1F. ‎ ‎【答案】详见解析 考点：直线与直线、平面与平面位置关系 ‎【名师点睛】垂直关系证明中应用转化与化归思想的常见类型.‎ ‎(1)证明线面垂直，需转化为证明线线垂直.‎ ‎(2)证明线线垂直，需转化为证明线面垂直.‎ ‎(3)证明面面垂直，需转化为证明线面垂直，进而转化为证明线线垂直. ‎ 考点 了解A 掌握B 灵活运用C 直线与平面垂直的判定及性质 B 高考对这部分的考查主要集中在以下几个方面：1、常融合平行、垂直等多种关系于一体考察，以选择题居多；2、直接考查证明直线与平面垂直，常在解答题中的第一问考查； 3、以线面垂直的探讨性问题居多，一般以是否存在某定点的形式考察，常在解答题中的第二问考查。 ‎ ‎1．直线与平面垂直 ‎(1)定义 如果直线l与平面α内的任意一条直线都垂直，则直线l与平面α垂直．‎ ‎(2)判定定理与性质定理 文字语言 图形语言 符号语言 判定定理 一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直 ⇒l⊥α 性质定理 垂直于同一个平面的两条直线平行 ⇒a∥b ‎2.直线和平面所成的角 ‎(1)定义 平面的一条斜线和它在平面上的射影 所成的锐角，叫做这条直线和这个平面所成的角．若一条直线垂直于平面，它们所成的角是直角，若一条直线和平面平行，或在平面内，它们所成的角是0°的角．‎ ‎(2)范围：[0，]．‎ ‎3．平面与平面垂直 ‎(1)二面角的有关概念 ‎①二面角：从一条直线出发的两个半平面所组成的图形叫做二面角；‎ ‎②二面角的平面角：在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的两条射线，这两条射线所构成的角叫做二面角的平面角．‎ ‎(2)平面和平面垂直的定义 两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．‎ ‎(3)平面与平面垂直的判定定理与性质定理 文字语言 图形语言 符号语言 判定定理 一个平面过另一个平面的垂线，则这两个平面垂直 ⇒α⊥β 性质定理 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直 ⇒l⊥α 题型一　直线与平面垂直的判定与性质 例1　(2016·全国甲卷改编)如图，菱形ABCD的对角线AC与BD交于点O，AB＝5，AC＝6，点E，F分别在AD，CD上，AE＝CF＝，EF交BD于点H.将△DEF沿EF折到△D′EF的位置．OD′＝.‎ 证明：D′H⊥平面ABCD.‎ ‎【答案】见解析 于是D′H2＋OH2＝32＋12＝10＝D′O2，故D′H⊥OH.‎ 又D′H⊥EF，而OH∩EF＝H，且OH，EF⊂平面ABCD，‎ 所以D′H⊥平面ABCD.‎ 解题技巧与方法总结 证明线面垂直的常用方法及关键 ‎(1)证明直线和平面垂直的常用方法有：①判定定理；②垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；③面面平行的性质(a⊥α，α∥β⇒a⊥β)；④面面垂直的性质．‎ ‎(2)证明线面垂直的关键是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．‎ ‎【变式训练】(2015·江苏)如图，在直三棱柱ABCA1B1C1中，已知AC⊥BC，BC＝CC1.设AB1‎ 的中点为D，B1C∩BC1＝E.‎ 求证：(1)DE∥平面AA1C1C；‎ ‎(2)BC1⊥AB1.‎ ‎【答案】见解析 因为BC＝CC1，所以矩形BCC1B1是正方形，‎ 因此BC1⊥B1C.‎ 因为AC，B1C⊂平面B1AC，AC∩B1C＝C，‎ 所以BC1⊥平面B1AC.‎ 又因为AB1⊂平面B1AC，‎ 所以BC1⊥AB1. ‎ 题型二　平面与平面垂直的判定与性质 例2　如图，四棱锥P－ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．‎ ‎(1)求证：CE∥平面PAD；‎ ‎(2)求证：平面EFG⊥平面EMN.‎ ‎【答案】见解析 ‎【解析】证明　(1)方法一　‎ 取PA的中点H，连接EH，DH.‎ 又E为PB的中点，‎ 所以EH綊AB.‎ 又CD綊AB，‎ 所以EH綊CD.‎ 所以四边形DCEH是平行四边形，所以CE∥DH.‎ 又DH⊂平面PAD，CE⊄平面PAD.‎ 所以CE∥平面PAD.‎ 方法二　‎ 连接CF.‎ 因为F为AB的中点，‎ 所以AF＝AB.‎ 又CD＝AB，所以AF＝CD.‎ 又AF∥CD，所以四边形AFCD为平行四边形．‎ 因此CF∥AD，又CF⊄平面PAD，AD⊂平面PAD，‎ 所以CF∥平面PAD.‎ 引申探究 ‎1．在本例条件下，证明：平面EMN⊥平面PAC.‎ ‎【答案】见解析 ‎【解析】证明　因为AB⊥PA，AB⊥AC，‎ 且PA∩AC＝A，所以AB⊥平面PAC.‎ 又MN∥CD，CD∥AB，所以MN∥AB，‎ 所以MN⊥平面PAC.‎ 又MN⊂平面EMN，‎ 所以平面EMN⊥平面PAC.‎ ‎2．在本例条件下，证明：平面EFG∥平面PAC.‎ ‎【答案】见解析 ‎【解析】证明　因为E，F，G分别为PB，AB，BC的中点，‎ 所以EF∥PA，FG∥AC，‎ 又EF⊄平面PAC，PA⊂平面PAC，‎ 所以EF∥平面PAC.‎ 同理，FG∥平面PAC.‎ 又EF∩FG＝F，‎ 所以平面EFG∥平面PAC. ‎ 解题技巧与方法总结 ‎ (1)判定面面垂直的方法 ‎①面面垂直的定义；‎ ‎②面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．‎ ‎(2)在已知平面垂直时，一般要用性质定理进行转化．‎ 在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．‎ ‎【变式训练】(2016·江苏)如图，在直三棱柱ABCA1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.‎ 求证：(1)直线DE∥平面A1C1F；‎ ‎(2)平面B1DE⊥平面A1C1F.‎ ‎【答案】见解析 ‎∴平面B1DE⊥平面A1C1F. ‎ 题型三　垂直关系中的探索性问题 例3　如图，在三棱台ABC－DEF中，CF⊥平面DEF，AB⊥BC.‎ ‎(1)设平面ACE∩平面DEF＝a，求证：DF∥a；‎ ‎(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在，请确定G点的位置；若不存在，请说明理由．‎ ‎【答案】见解析 此时，如平面图所示，延长CB，FG交于点H，‎ ‎∵O为CE的中点，EF＝CF＝2BC，‎ 由平面几何知识易证△HOC≌△FOE，‎ ‎∴HB＝BC＝EF.‎ 由△HGB∽△FGE可知＝，即BG＝BE.‎ 解题技巧与方法总结 同“平行关系中的探索性问题”的规律方法一样，一般是先探求点的位置，多为线段的中点或某个三等分点，然后给出符合要求的证明．‎ ‎【变式训练】(2016·北京东城区模拟)如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，M为棱AC的中点．AB＝BC，AC＝2，AA1＝.‎ ‎(1)求证：B1C∥平面A1BM；‎ ‎(2)求证：AC1⊥平面A1BM；‎ ‎(3)在棱BB1上是否存在点N，使得平面AC1N⊥平面AA1C1C？如果存在，求此时的值；如果不存在，请说明理由．‎ ‎【答案】见解析 ‎∴OM∥B1C，‎ 又∵OM⊂平面A1BM，B1C⊄平面A1BM，‎ ‎∴B1C∥平面A1BM.‎ ‎ ‎ ‎(3)解　当点N为BB1中点，即＝时，‎ 平面AC1N⊥平面AA1C1C.‎ 证明如下：‎ 设AC1中点为D，连接DM，DN.‎ ‎∵D，M分别为AC1，AC中点，‎ ‎∴DM∥CC1，且DM＝CC1.‎ 又∵N为BB1中点，∴DM∥BN，且DM＝BN，‎ ‎∴四边形BNDM为平行四边形，‎ ‎∴BM∥DN，‎ ‎∵BM⊥平面ACC1A1，∴DN⊥平面ACC1A1.‎ 又∵DN⊂平面AC1N，∴平面AC1N⊥平面AA1C1C.‎ ‎1.（吉林省实验中学2016-2017学年度高二下学期期末）在如图所示的几何体中，底面ABCD中，AB⊥AD，AD＝2，AB＝3，BC＝BE＝7，△DCE是边长为6的正三角形．‎ ‎(1)求证：平面DEC⊥平面BDE；‎ ‎(2)求点A到平面BDE的距离．‎ ‎【答案】（1）见解析；（2）．‎ ‎ ‎ ‎(2)解　如图，取CD的中点O，连接OE，‎ 因为△DCE是边长为6的正三角形，‎ 所以EO⊥CD，EO＝3，‎ 易知EO⊥平面ABCD，‎ 则VE－ABD＝××2×3×3＝3，‎ 又因为直角三角形BDE的面积为×6×＝3，‎ 设点A到平面BDE的距离为h，则由VE－ABD＝VA－BDE，‎ 得×3h＝3，所以h＝，所以点A到平面BDE的距离为．‎ ‎【点睛】在求几何体体积时常有两种方法：(1)割补法：求一些不规则几何体的体积时，常用割补法转化成已知体积公式的几何体进行解决.(2)等积法：等积法包括等面积法和等体积法.等体积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到，利用等积法可以用来求解几何图形的高或几何体的高.‎ ‎2．（安徽省亳州市二中2017届高三下学期教学质量检测）如图所示，四棱锥，已知平面平面， ．‎ ‎（I）求证： ；‎ ‎（II）若，求三棱锥的体积．‎ ‎【答案】（1）见解析（2） ‎（II） 中边上的高长为．‎ ，‎ 由（I）知，三棱锥底面上的高长为，‎ ．‎ 点睛：求三棱锥的体积时要注意三棱锥的每个面都可以作为底面，例如三棱锥的三条侧棱两两垂直，我们就选择其中的一个侧面作为底面，另一条侧棱作为高来求体积．‎ ‎3．（北京市昌平区2017年高三第二次统一练习）在四棱锥中， 为正三角形，平面平面， ， ， .‎ ‎（Ⅰ）求证：平面平面； ‎ ‎（Ⅱ）求三棱锥的体积；‎ ‎（Ⅲ）在棱上是否存在点，使得平面?若存在，请确定点的位置并证明；若不存在，说明理由．‎ ‎【答案】(1)证明见解析；（2）；（3）存在，证明见解析.‎ ‎ ‎ 所以 .‎ ‎（Ⅲ）在棱上存在点，当为的中点时， 平面.‎ 分别取的中点，连结.‎ 所以. 因为， ，‎ 所以.‎ 所以四边形为平行四边形.‎ 所以.‎ 因为,‎ 所以平面平面.‎ 因为平面，‎ 所以平面. ‎ ‎4．（四川省成都七中实验学校2016-2017学年高二下学期期中）如图，在三棱柱中侧棱垂直于底面， ，点是的中点。‎ ‎（Ⅰ）求证： ； ‎ ‎（Ⅱ）求证： 平面。‎ ‎【答案】(1) 详见解析;(2) 详见解析.‎ ‎ ‎ ‎（Ⅱ）设与的交点为，连结，‎ 为平行四边形，所以为中点，‎ 又是的中点，所以是三角形的中位线， ， ‎ 又因为平面， 平面，所以平面 点睛：垂直、平行关系证明中应用转化与化归思想的常见类型.‎ ‎(1)证明线面、面面平行，需转化为证明线线平行.‎ ‎(2)证明线面垂直，需转化为证明线线垂直.‎ ‎(3)证明线线垂直，需转化为证明线面垂直. ‎ ‎5．（河南省新乡市2017届高三第三次模拟）如图，边长为2的正方形和高为2的直角梯形所在的平面互相垂直， ， ， 且.‎ ‎（1）求证： 平面；‎ ‎（2）过作平面，垂足为，求三棱锥的体积.‎ ‎【答案】（1）见解析;（2）.‎ ‎ ‎ ‎ 6．（四川省遂宁市2017届高三三诊考试）如图，在直三棱柱ABC—A1B1C1中，AB=BC=BB1， ，D为AC上的点，B1C∥平面A1BD；‎ ‎（1）求证：BD⊥平面；‎ ‎（2）若且，求三棱锥A-BCB1的体积．‎ ‎【答案】（1）见解析;（2） ‎【解析】【试题分析】（１）运用线面垂直判定定理推证；（２）先求三棱锥的高与底面面积再运用三棱锥的体积公式求解：‎ ‎（1）连结ED， ‎ ‎∵平面AB1C∩平面A1BD=ED，B1C∥平面A1BD，‎ ‎∴B1C∥ED， ‎ ‎∵E为AB1中点，∴D为AC中点， ‎ ‎∵AB=BC， ∴BD⊥AC①‎ ‎ ‎ ‎7．（湖南省长沙市雅礼中学2017届高考模拟）如图，四边形为菱形， 为与的交点， 平面．‎ ‎（1）证明：平面平面；‎ ‎（2）若，三棱锥的体积为，求该三棱锥的侧面积（平面为底面）．‎ ‎【答案】(1)证明见解析；(2) ．‎ 考点：1．平面与平面平行的判定定理；2．空间几何体的侧面积和体积．‎ ‎【易错点睛】本题主要考查立体几何中线面之间的位置关系,以及表面积和体积的计算,属于中档题． 在(1)中,要证明面面垂直,而由面面垂直的判定定理:如果一个平面经过另外一个平面的一条垂线,那么这两个平面互相垂直,即由线面垂直得到面面垂直．由, ,得出平面,又平面，所以平面平面．在(2)中,利用三棱锥的体积为,求出的长度,再求出个侧面的面积,它们的和即为三棱锥的侧面积．‎ ‎8．（山西省临汾一中、忻州一中、长治二中、康杰中学2016-2017学校高二4月联考）如图，在各棱长为的直四棱柱中，底面为棱形， 为棱上一点，且 ‎（1）求证：平面平面；‎ ‎（2）平面将四棱柱分成上、下两部分，求这两部分的体积之比. ‎ ‎（棱台的体积公式为，其中分别为上、下底面面积， 为棱台的高）‎ ‎【答案】（1）证明见解析；（2）.‎ ‎（2）解：连接，过作交于，则 则平面与侧面相交的线段为 故平面将四棱柱分成上、下两部分中的上部分由三棱台组成，‎ 取的中点,连接 底面为菱形， 为正三角形，即也为正三角形， 又底面 平面 又四棱柱的体积为 ‎ ‎