- 2021-06-17 发布 |
- 37.5 KB |
- 6页

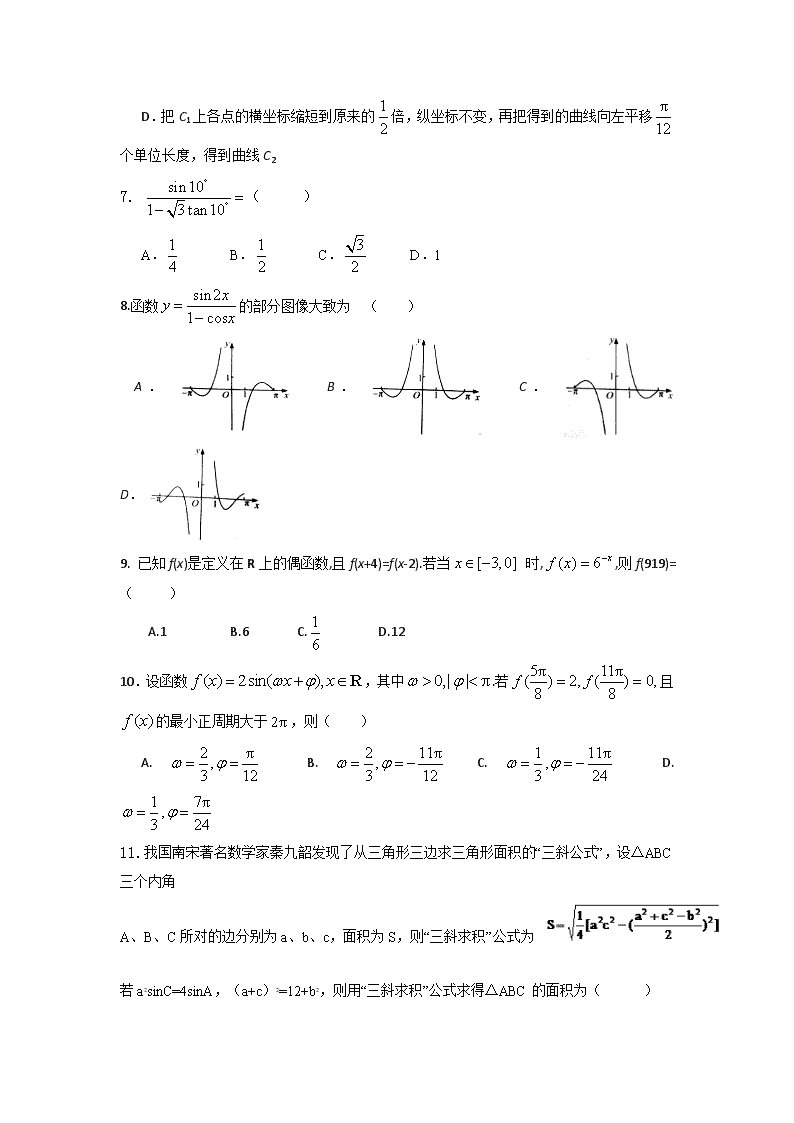

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届重庆市万州分水中学高三9月月考(2017
分水中学高2018级高三上期9月月考 数学试题(文科) 一、选择题:(本大题共12小题,每小题5分,共60分) 1.已知集合A=,B=,则 ( ) A.AB= B.AB C.AB D.AB=R 2. 复数的共轭复数为 ( ) A. B. C. D. 3.若x>2m2﹣3是﹣1<x<4的必要不充分条件,则实数m的取值范围是( ) A.[﹣3,3] B.(﹣∞,﹣3]∪[3,+∞) C.(﹣∞,﹣1]∪[1,+∞) D.[﹣1,1] 4.阅读如图所示的程序框图,运行相应的程序,输出的n的值为( ) A.1 B.2 C.3 D.4 5.函数y=的定义域是( ) A. B. C. D. 6.已知曲线C1:y=cos x,C2:y=sin (2x+),则下面结论正确的是( ) A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2 B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2 C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2 D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2 7. ( ) A. B. C. D.1 8.函数的部分图像大致为 ( ) A. B. C. D. 9. 已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当 时,,则f(919)=( ) A.1 B.6 C. D.12 10.设函数,其中.若且的最小正周期大于,则( ) A. B. C. D. 11.我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”,设△ABC三个内角 A、B、C所对的边分别为a、b、c,面积为S,则“三斜求积”公式为 若a2sinC=4sinA,(a+c)2=12+b2,则用“三斜求积”公式求得△ABC的面积为( ) A. B.2 C.3 D. 12.已知函数,若存在,使得,则实数的取值范围是 ( ) A. B. C. D. 二、填空题:(本大题共4小题,每小题5分,共20分) 13.若 则 . 14.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=,A=,则角B等于_______. 15.已知点P是抛物线上的点,且点P到原点的距离为,则点P到该抛物线焦点的距离为 . 16.已知函数f(x)=其中m>0.若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是_______ . 三、解答题(本大题共6小题,共70分,写出必要的计算、证明或推理过程) 17.在△ABC中, =60°,c=a. (Ⅰ)求sinC的值; (Ⅱ)若a=7,求△ABC的面积。 18. 已知函数。 (Ⅰ)f(x)的最小正周期; (Ⅱ)求证:当时, 。 19. “微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下: (1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关? 附: , 0.10 0.05 0.025 0.010 2.706 3.841 5.024 6.635 (2)若想在步数大于10000的学生中分层选取5位学生进行身体状况调查,然后再从这5位学生中选取2位进行面对面的交流,求这2位学生至少有一位女生的概率. 20. 已知函数 (1)求函数的定义域。 (2)若函数在上单调递增,求实数的取值范围。 21. 已知函数,其中. (1)设是的导函数,求函数的极值; (2)是否存在常数,使得在恒成立,且在有唯一解,若存在,求出的值;若不存在,说明理由。 以下任选一题 22. (本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系xOy中,直线L的参数方程是(t为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ2cos2θ+2ρ2sin2θ=12,且直线与曲线C交于P,Q两点。 (1)求曲线C的普通方程及直线L恒过的定点A的坐标; (2)在(1)的条件下,若|AP||AQ|=6,求直线L的普通方程。 23. (本小题满分10分)选修4-5:不等式选讲 函数f(x)=|x﹣a|,a<0 (Ⅰ)若a=﹣2求不等式f(x)+f(2x)>2的解集; (Ⅱ)若不等式f(x)+f(2x)<的解集非空,求a的取值范围。 查看更多