- 2021-06-16 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
广东省六校联盟2020届高三下学期第四次联考数学(理)试题 Word版含解析
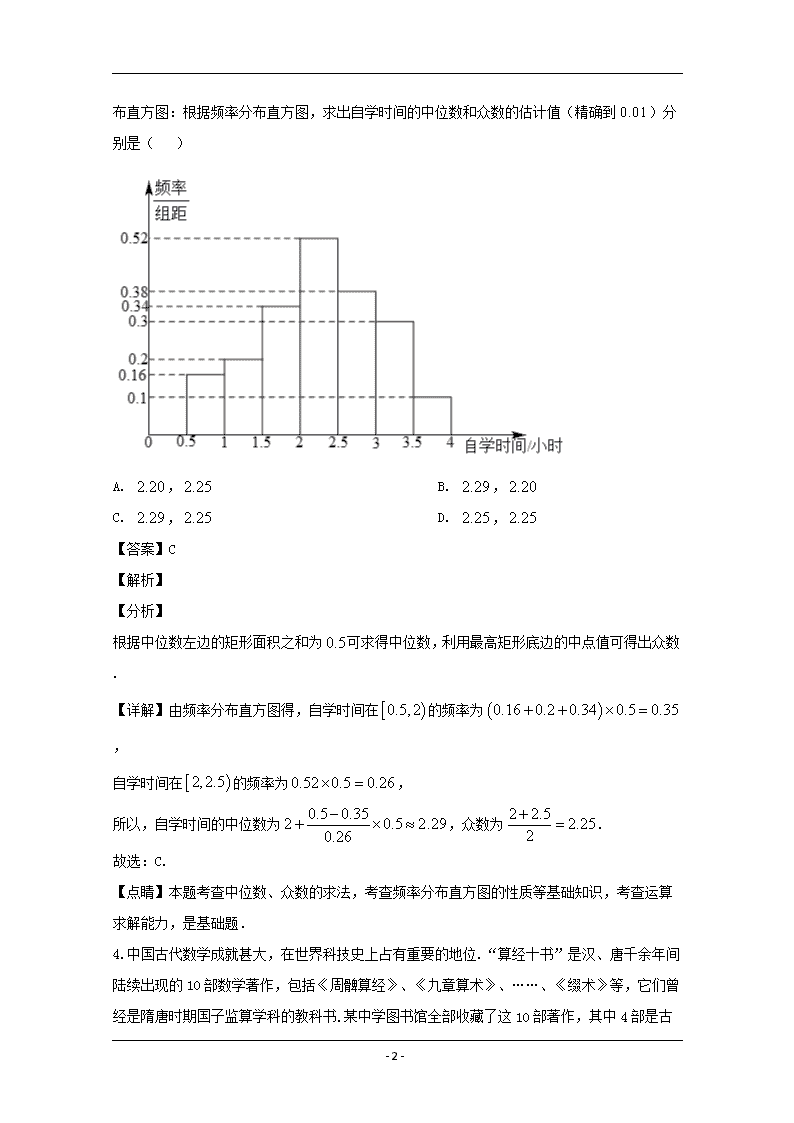
- 1 - 六校联盟 2020 届高三第四次联考 理科数学试卷 一、单选题 1. 设 2 i i z ,则 z的共轭复数 z在复平面内的对应点在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】B 【解析】 【分析】 利用复数的除法的运算法则和共轭复数的定义进行求解即可. 【详解】 2 (2 ) 1 2iz i i i i , 1 2z i . 故选:B 【点睛】本题考查了复数的除法运算的法则,考查了共轭复数的定义,考查了复数在复平面 的位置特征,考查了数学运算能力. 2. 记全集U R ,集合 2| 16A x x ,集合 | 2 2xB x ,则 U A B ð ( ) A. 4, B. 1,4 C. 1,4 D. 1,4 【答案】C 【解析】 【分析】 求得集合 { | 4A x x 或 4}x , { | 1}B x x ,求得 { | 4 4}U A x x ð ,再结合集 合的交集运算,即可求解. 【详解】由题意,全集U R ,集合 2| 16 { | 4A x x x x 或 4}x , 集合 | 2 2 { | 1}xB x x x , 所以 { | 4 4}U A x x ð ,所以 { |1 4} 1,4U A B x x ð . 故选:C. 【点睛】本题主要考查了集合的混合运算,其中解答中正确求解集合 ,A B,再结合集合的补 集和交集的运算求解是解答的关键,着重考查了推理与运算能力,属于基础题. 3. 如图是某学校的教研处根据调查结果绘制的本校学生每天放学后的自学时间情况的频率 - 2 - 分布直方图:根据频率分布直方图,求出自学时间的中位数和众数的估计值(精确到0.01) 分别是( ) A. 2.20, 2.25 B. 2.29,2.20 C. 2.29, 2.25 D. 2.25,2.25 【答案】C 【解析】 【分析】 根据中位数左边的矩形面积之和为 0.5可求得中位数,利用最高矩形底边的中点值可得出众 数. 【详解】由频率分布直方图得,自学时间在 0.5,2 的频率为 0.16 0.2 0.34 0.5 0.35 , 自学时间在 2,2.5 的频率为0.52 0.5 0.26 , 所以,自学时间的中位数为 0.5 0.352 0.5 2.29 0.26 ,众数为 2 2.5 2.25 2 . 故选:C. 【点睛】本题考查中位数、众数的求法,考查频率分布直方图的性质等基础知识,考查运算 求解能力,是基础题. 4. 中国古代数学成就甚大,在世界科技史上占有重要的地位.“算经十书”是汉、唐千余年 间陆续出现的 10 部数学著作,包括《周髀算经》、《九章算术》、……、《缀术》等,它们曾经 是隋唐时期国子监算学科的教科书.某中学图书馆全部收藏了这 10 部著作,其中 4 部是古汉 语本,6部是现代译本,若某学生要从中选择 2部作为课外读物,至少有一部是现代译本的概 - 3 - 率是( ) A. 13 15 B. 2 3 C. 8 15 D. 1 3 【答案】A 【解析】 【分析】 求出从 10 部著作中选择 2部古汉语本的方法数,即 2部都不是现代译本的方法数,由对立事 件的概率计算公式,可得结论. 【详解】解:从 10 部著作中选择 2 部著作的方法数为 2 10 45C (种), 2部都不是现代译本的方法数为 2 4 6C (种), 由对立事件的概率计算公式得至少有一部是现代译本的概率 1 45 6 13 15 P . 故选:A. 【点睛】本题考查概率的计算,考查组合知识,属于基础题. 5. 己知 1sin 5 4 ,则 3cos 2 5 ( ) A. 7 8 B. 7 8 C. 1 8 D. 1 8 【答案】A 【解析】 【分析】 本题首先可以根据诱导公式以及二倍角公式对 3cos 2 5 进行化简,然后代入 1sin 5 4 ,即可得出结果. 【详解】因为 1sin 5 4 , 所以 3 2 2cos 2 cos 2 cos 2 5 5 5 22cos 2 1 2sin 5 5 - 4 - 21 71 2 4 8 轾 骣犏 琪= - - ´ = - 犏 桫臌 故选:A. 【点睛】本题考查诱导公式以及二倍角公式的灵活应用,考查的公式有 cos cos 、 cos cos 以及 2cos 2 1 2sin ,考查化归与转化思想,是中档题. 6. 函数 2 x xy e 的图象大致是( ) A. B. C. D. 【答案】A 【解析】 【分析】 根据函数有两个极值点,可排除选项 C、D;利用奇偶性可排除选项 B,进而可得结果. - 5 - 【详解】因为 2 x xy e ,所以 22' x x xy e , 令 ' 0y 可得, 0, 2x x , 即函数有且仅有两个极值点,可排除选项 C、D; 又因为函数 2 x xy e 即不是奇函数,又不是偶函数,可排除选项 B, 故选:A. 【点睛】函数图象的辨识可从以下方面入手: (1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象. 7. 中国古代数学著作《算法统宗》中有这样一个“九儿问甲歌”问题:一个公公九个儿,若 问生年总不知,自长排来差三岁,共年二百又零七,借问长儿多少岁,各儿岁数要详推.在 这个问题中,记这位公公的第 n个儿子的年龄为 na ,则 3 4 5 6 7 1 9a a a a a a a ( ) A. 46 B. 69 C. 92 D. 138 【答案】B 【解析】 由题意得数列成等差数列,公差为-3,所以 9 1 1 19 9 8 ( 3) 207 35; 2 S a a 3 4 5 6 7 1 9a a a a a a a 13 12 69.a d 选 B. 8. 元旦将近,调查鲜花市场价格得知:购买 2只玫瑰与 1 只康乃馨所需费用之和大于 8元, 而购买 4 只玫瑰与 5 只康乃馨所需费用额小于 22 元;设购买 2 只玫瑰花所需费用为 A元,购 买 3 只康乃馨所需费用为 B元,则 A B、的大小关系是( ). A. A B B. A B C. A B D. A B、的大 小关系不确定 【答案】A 【解析】 【分析】 - 6 - 设出玫瑰与康乃馨的单价,根据题意列出不等式,求出 A B、的表达式,利用不等式的性质求 解即可. 【 详 解 】 设 玫 瑰 与 康 乃 馨 的 单 价 分 别 为 ,x y ( 单 位 为 : 元 ) , 则 有 2 8 ,2 ,3 4 5 22 x y x A y B x y . 所以有 , 2 3 A Bx y ,因此 8(1) 3 52 22(2) 3 BA BA . (1) 5 (2) ( 1) 可得: 6A ; (1) 2 (2) ( 1) 可得: 6B ,因此 A B . 故选:A 【点睛】本题考查了数学阅读能力,考查了不等式性质的应用,考查了数学建模思想,考查 数学运算能力. 9. 设 F 为双曲线 2 2 2 2: 1 0, 0x yC a b a b 的右焦点,过坐标原点的直线依次与双曲线C 的左、右支交于点 P、Q,若 2PQ QF , 60PQF ,则该双曲线的离心率为( ) A. 3 1 B. 3 C. 2 D. 3 2 【答案】A 【解析】 【分析】 根据题意,得到 90PFQ ,设双曲线的左焦点为 1F,连接 1FP, 1FQ,根据对称性,得 到:四边形 1F PFQ是矩形,再由 1 1 2 2 F Fce a QF QF ,即可求出结果. 【详解】因为 2PQ QF , 60PQF , 由余弦定理可得: 2 2 2 2 cosPF PQ QF PQ QF PQF 2 2 25 2 3QF QF QF ,即 3PF QF , - 7 - 所以 2 2 2PF QF PQ ,因此 90PFQ , 设双曲线的左焦点为 1F,连接 1FP, 1FQ, 由对称性可得:四边形 1F PFQ是矩形,且 1 2 2FF QF c , 1 3 3QF QF c , 故离心率为 1 1 2 2 3 1 2 3 F Fc ce a QF QF c c . 故选:A. 【点睛】本题主要考查求双曲线的离心率,熟记双曲线的简单性质即可,属于常考题型. 10. 在边长为 2 3的菱形 ABCD 中, 60A ,沿对角线 BD 折起,使二面角 A BD C 的大 小为120,这时点 A、B、C、D 在同一个球面上,则该球的表面积为( ) A. 36 B. 28 C. 24 D. 16 【答案】B 【解析】 【分析】 正确做出图形,利用勾股定理建立方程,求出四面体的外接球半径,即可求出四面体的外接 球的表面积. 【详解】解:根据题意画出图形,如图所示: - 8 - 如图分别取BD AC、 的中点M、N ,连接MN AM CM、 、 , 则 2 3AB BD DC BC , ,AM BD CM BD , 所以 AMC 为二面角 A BD C 的平面角,所以 120AMC . 由题知 ,ABD BCD 为等边三角形,所以 3AM CM , 3MD . 2 2 2 2 2 12 cos120 3 3 2 3 3 27 2 AC AM CM AM CM , 所以 AC 3 3 ,所以 3 3 3, 2 2 MN CN . 由图形的对称性可知:球心必在MN的延长线上,设球心为O,连接OC OD、 ,设半径为 R, ON x ,OC OD R 。 可知: ONC△ , OMD 为直角三角形, 所以 2 2 2 2 2 2 OC ON NC OD OM MD ,所以 2 2 2 2 27 4 3 3 2 R x R x , 解得: 1 2 x , 2 7R , 所以球的表面积为: 24 4 7 28S R . 故选:B. 【点睛】本题主要考查四面体的外接球的表面积,考查学生的计算能力,属于中档题. 11. 己知函数 2sin 0, 2 f x x 图象过点 0, 1B ,且在区间 , 18 3 - 9 - 上单调.又 f x 的图象向左平移 个单位之后与原来的图象重合,当 1 2 17 2, , 12 3 x x ,且 1 2x x 时, 1 2f x f x ,则 1 2f x x ( ) A. 3 B. 2 C. 1 D. -1 【答案】D 【解析】 【分析】 根据题意先求得 , 的值,然后写出函数 f x 的解析式,求 f x 图象的对称轴,得 1 2x x 的值,再求 1 2f x x 的值. 【详解】解:因为函数 2sinf x x 图象过点 0, 1B , 12sin 1 sin 2 , 又 2 , 6 , 又函数 f x 在区间 , 18 3 上单调, 且 f x 的图象向左平移 个单位之后与原来的图象重合, 1 2 3 18 2 2k 18 5 2 ( )k k Z , 2 ,此时 1k . 2sin 2 6 f x x , 令2 6 2 x k ,解得 2 3 kx , f x 的对称轴为 2 3 kx , k Z , 1 2 17 2, , 12 3 x x ,且 1 2x x 时, 1 2f x f x , 1 2 17 4, 6 3 x x ,且 1 2 , 2 2 3 x x k k Z , - 10 - 当 3k 时符合题意, 此时 1 2 3 7 2 2 3 6 x x , 1 2 7 3 x x , 1 2 7 29 12sin 2 2sin 2 1 3 6 6 2 f x x 故选:D 【点睛】本题考查三角函数的图象变换和性质的应用问题,考查理解辨析能力与运算求解能 力,属于综合题. 12. 己知函数 3 sinf x x x , 1 1, 0 2 ln 1 , 0 x x g x x x ,若关于 x 的方程 0f g x m 有两个不等实根 1x , 2x ,且 1 2x x ,则 2 1x x 的最小值是( ) A. 2 B. 3 ln 2 C. 4 2ln 2 D. 3 2 ln 2 【答案】D 【解析】 【分析】 先判断出函数 f x 的奇偶性和单调性,令 t xg ,由题意结合函数 y g x 的图象即可 知 f t m 仅在 0,1 上有一解,再根据 y g x 的解析式求出 1x , 2x ,得到 2 1 2 1tx x e t ,然后构造函数 2 1, 0,1tt e t t ,利用导数即可求出函数的最 小值. 【详解】因为函数 f x 的定义域为R,且 3 sinf x x x f x ,所以函数 f x 为奇函数.考虑函数 f x 在 0,x 上的单调性,由于 23 cosf x x x , 当 0,1x , cos 0x ,∴ 23 cos 0f x x x ;当 1,x 时, 23 3x , 1 cos 1x ,∴ 23 cos 0f x x x ,即当 0,x 时,总有 0f x . 故函数 f x 在 0,x 上单调递增,而函数 f x 为奇函数,即函数 f x 在R上递增. 令 t xg ,作出函数 y g x 的图象,如图所示: - 11 - 由图以及题意可知, f t m 仅在 0,1 上有一解,即 0,1t . 由 t xg 解得, 1 2 1x t , 2 1tx e ,即有 2 1 2 1tx x e t . 设 2 1, 0,1tt e t t , ∵ 2tt e ,∴当 0, ln 2t 时, 0t ,当 ln 2,1t 时, 0t . 所以, min ln 2 3 2ln 2 . 故选:D. 【点睛】本题主要考查函数的性质奇偶性和单调性的应用,方程的根与两函数的图象的交点 之间的关系应用,以及利用导数求函数的最值,意在考查学生的转化能力,直观想象能力和 数学运算能力,属于中档题. 二、填空题 13. 如图,在△ ABC中, 90A , 3AB ,D在斜边 BC上,且 2CD DB ,则 AB AD 的值为________ 【答案】6 【解析】 【分析】 以 ,AB AC 为基底,表示出向量 AD ,利用数量积计算即可求值. 【详解】由题意, AD AB BD , 因为 2CD DB , - 12 - 所以 1 3 BD BC , 所以 1 1 2 1( ) 3 3 3 3 AD AB BD AB BC AB AC AB AB AC , 2 22 1 2 1 2) 3 0 6 3 3 3 ( 3 3 AB AC AB AAB AD B ACAB , 故答案为:6 【点睛】本题主要考查了向量的线性运算,向量的数量积的运算性质,属于中档题. 14. 若二项式 1 n x x 展开式中各项系数的和为 64,则该展开式中常数项为____________. 【答案】15 【解析】 二项式 1 n x x 展开式中各项系数的和为 64,令 1x ,得 6 12 64, 8,n n x x 的通项为 366 2 2 1 6 6 r rr r r rT C x x C x ,令 36 0, 4 2 r r ,常数项为 4 6 15C ,故答案为 15 . 【方法点晴】本题主要考查二项展开式定理的通项、系数及各项系数和的求法,属于简单题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要 从以下几个方面命题:(1)考查二项展开式的通项公式 1 Cr n r r r nT a b ;(可以考查某一项, 也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理 的应用. 15. 如图,将数列 na 中的所有项按每一行比上一行多两项的规则排成数表,已知表中的第 一列 1a 、 2a 、 5a 、构成一个公比为 2的等比数列,从第 2行起,每一行都是一个公差为 d 的等差数列,若 3 5a , 86 524a ,则 d ________. 【答案】3 【解析】 - 13 - 【分析】 本题首先可根据题意得出每一行中所包含的数列 na 中的项,然后根据每一行都是一个公差 为 d 的等差数列得出 2 5a d 、 82 524 4a d ,再然后根据表中的第一列 1a 、 2a 、 5a 、 构成一个公比为2的等比数列得出 8 2 822a a´ = ,最后通过计算即可得出结果. 【详解】由题意可知,第一行是 1a ,第二行是从 2a 到 4a ,第三行是从 5a 到 9a ,第四行是从 10a 到 16a ,第五行是从 17a 到 25a ,第六行是从 26a 到 36a ,第七行是从 37a 到 49a ,第八行是从 50a 到 64a ,第九行是从 65a 到 81a ,第十行是从 82a 到 100a , 故 3a 在第二行, 86a 在第十行, 因为 3 5a , 86 524a ,每一行都是一个公差为 d 的等差数列, 所以 2 5a d , 82 524 4a d , 因为表中的第一列 1a 、 2a 、 5a 、构成一个公比为2的等比数列, 所以 8 2 822a a´ = ,即( ) 85 2 524 4d d- ´ = - ,解得 3d , 故答案为3 . 【点睛】本题考查等差数列以及等比数列的综合应用,能否根据题意明确每一行中所包含的 数列 na 中的项是解决本题的关系,考查推理能力与计算能力,是简单题. 16. 长方体 1 1 1 1ABCD ABC D 中, 2AB , 1BC , 1 2AA ,P为该长方体侧面 1 1CC D D 内(含边界)的动点,且满足 tan tan 2 2PAD PBC ,则四棱锥P ABCD 体积的取 值范围是________. 【答案】 2 2, 3 3 【解析】 【分析】 首先可以绘出长方体 1 1 1 1ABCD ABC D 的图像,然后根据 tan tan 2 2PAD PBC 得 出 2 2PD PC ,根据椭圆定义即可得出点 P的轨迹,然后构建直角坐标系并绘出椭圆图 - 14 - 像,结合图像即可求出 maxh 以及 minh ,最后通过棱锥的体积计算公式即可得出结果. 【详解】如图,绘出长方体 1 1 1 1ABCD ABC D , 因为 P为该长方体侧面 1 1CC D D内(含边界)的动点, 所以 AD PD ,BC PC , 因为 tan tan 2 2PAD PBC , 1BC AD 所以 2 2PD PC AD CB + = , 2 2PD PC , 故点 P的轨迹为在侧面 1 1CC D D内(含边界)、以D点和C点为焦点的椭圆, 则2 2 2a , 1c , 2 2 1b a c ,椭圆方程为 2 2 1 2 x y , 以DC为 x轴、DC中点为原点构建直角坐标系,并绘出椭圆图像,如图: 当点 P在椭圆上顶点时,点 P到底面 ABCD的距离 h最大, max 1h = ; 当点 P在椭圆与棱 1DD 或棱 1CC 交点时,点 P到底面 ABCD的距离 h最小, 令 1x ,解得 2 2 y , min 2 2 h = , 故四棱锥 P ABCD 体积的最大值 max 1 22 1 1 3 3 V = 创 � , 四棱锥P ABCD 体积的最小值 min 1 2 22 1 3 2 3 V = 创 � , - 15 - 四棱锥P ABCD 体积的取值范围是 2 2, 3 3 , 故答案为: 2 2, 3 3 . 【点睛】本题考查棱锥的体积的相关计算,考查椭圆的定义以及灵活应用,能否求出棱锥的 高的最值是解决本题的关键,考查计算能力,考查数形结合思想,是难题. 三、解答题 17. 如图,在 ABC 中,已知点D在边 AB上, 3AD DB , 4cos 5 A , 5cos 13 ACB , 13BC . (1)求 cosB的值; (2)求CD的长. 【答案】(1)(2) 【解析】 试题分析:根据平方关系由 cos A求出 sin A ,利用 cos ACB 求出 sin ACB ,根据三角形 内角和关系利用和角公式求出cosB,利用正弦定理求出 AB,根据 3AD DB ,计算 BD, 最后利用余弦定理求出CD . 试题解析:(1)在 ABC 中, 4cos 5 A , 0,πA , 所以 2 2 4 3sin 1 cos 1 5 5 A A . 同理可得, 12sin 13 ACB . 所以 cos cos π cosB A ACB A ACB sin sin cos cosA ACB A ACB - 16 - 3 12 4 5 16 5 13 5 13 65 . (2)在 ABC 中,由正弦定理得, 13 12sin 203sin 13 5 BCAB ACB A . 又 3AD DB ,所以 1 5 4 BD AB . 在 BCD 中,由余弦定理得, 2 2 2 cosCD BD BC BD BC B 2 2 165 13 2 5 13 9 2 65 . 【点睛】凑角求值是高考常见题型,凑角求知要“先备料”后代入求值,第二步利用正弦定 理和余弦定理解三角形问题,要灵活使用正、余弦定理,有时还要用到面积公式,注意边角 互化. 18. 如图,直角梯形 ABCD中, / /AB CD, 90BCD , 2BC CD , AD BD , EC 底面 ABCD, FD 底面 ABCD且有 2EC FD . (1)求证: AD BF ; (2)若线段 EC的中点为M ,求直线 AM与平面 ABEF所成角的正弦值. 【答案】(1)证明见解析;(2) 33 33 . 【解析】 【详解】试题分析:(1)根据线段长度的关系得到 AD BD , AD DF , BD、DF是平 面 BDF 内的相交直线, AD 平面 BDF ,进而得到线线垂直;(2)常用的方法是建系, 建立空间坐标系,求得直线的方向向量和面的法向量,根据向量的夹角公式得到线面角. 解析: (1) BC DC , 2BC CD - 17 - 2 2 2BD BC CD ,且 BCD 是等腰直角三角形, 45CDB CBD 平面 ABCD中, / /AB DC, 45DBA CBD AD BD ,可得 45DBA BAD 90ADB ,即 AD BD FD 底面 ABCD, AD底面 ABCD, AD DF BD、DF是平面 BDF 内的相交直线, AD 平面 BDF BF 平面 BDF , AD BF (2)解法一:几何法 如图,过点M 作MN BE ,垂足为 N ,连接NA, AC, AB BC , AB EC , BC EC E , AB 平面 BEC, MN 平面 BEC, AB MN 结合MN BE 且 BE AB BI ,可得MN 平面 ABEF AN 是 AM在平面 ABEF内的射影, 可得 MAN 就是直线 AM与平面 ABEF所成的角. Rt ABC 中, 2 2 10AC BC AB , Rt ACM 中, 2 2 11AM AC CM EMN EBC , MN EN BC EC , MN EM BC EB ,可得 3 3 MN 因此,在 RtMAN中, 33sin 33 MNMAN AM 即直线 AM与平面 ABEF所成角的正弦值是 33 33 . - 18 - 解法二:向量法 如图,以D点为坐标原点,直线DC为轴 y,DF为 z轴建立空间直角坐标系, 则 0,0,0D , 2, 2,0A , 2, 2,0B , 0, 2,1M , 0,0,2F , 所以: 2,2 2,1AM 0,2 2,0AB 2, 2,2AF 设平面 ABEF的一个法向量为 , ,n x y z ,由 2 2 0 2 2 2 0 n AB y n AF x y z 可取 2,0,1n cos , n AMn AM n AM 2 1 33 333 11 设直线 AM与平面 ABEF所成角为 ,则 , 2 n AM sin sin , 2 n AM 33cos , 33 n AM . 19. 己知动圆 C 过定点 1,0F ,且与定直线 1x 相切. - 19 - (1)求动圆圆心 C的轨迹 E的方程; (2)若过点 0,2M 的直线 l 与轨迹 E相交于 A,B 两点,N 为 AB 的中点,O 是坐标原点, 且 3AOB MONS S ,求直线 l 的方程. 【答案】(1) 2 4y x ;(2) l的方程为: 2y x 或 1 2 3 y x . 【解析】 【分析】 (1)结合抛物线的定义,求得轨迹 E的方程. (2)设出 , ,A B N的坐标,设出直线 l的方程 2 0y kx k ,联立直线的方程和轨迹 E的 方程,写出韦达定理,结合 3AOB MONS S 列方程,解方程求得 k,进而求得直线 l的方程. 【详解】(1)依题意动圆圆心 C 到定点 1,0F 的距离与到定直线 1x 的距离相等, 由抛物线的定义,可得动圆圆心 C 的轨迹是以 1,0F 为焦点, 1x 为准线的抛物线,其中 2p . ∴动圆圆心 C 的轨迹 E 的方程为 2 4y x . (2)设 1 1,A x y , 2 2,B x y , 0 0,N x y , 0,2M , 显然直线 l 的斜率存在, 设直线 : 2 0l y kx k ,联立 2 4 2 y x y kx , 消去 y 得 2 2 4 1 4 0k x k x , 因为 2 216 1 16 0k k ,得 1 2 k 且 0k , 所以 1 2 2 4 1 k x x k , 1 2 2 4x x k , 因为 3AOB MONS S ,所以 3AB MN , 所以 2 2 1 2 01 3 1 0k x x k x , 即 1 2 03x x x , - 20 - 因为 N 是 AB 的中点,所以 1 2 0 2 x xx , 所以 22 1 2 1 2 1 24 3 4 x x x x x x , 整理得 21 2 1 216x x x x , 所以 2 2 2 4 1 64k k k ,解得 1 1k , 2 1 3 k , 所以直线 l 的方程为: 2y x 或 1 2 3 y x . 【点睛】本小题主要考查动点轨迹方程的求法,考查直线和抛物线的位置关系,考查运算求 解能力,属于中档题. 20. 己知函数 sin cosf x x x x , cos xg x x . (1)判断函数 f x 在区间 50, 2 上零点的个数; (2)设函数 g x 在区间 0, 上的极值点从小到大分别为 1x , 2x , 3x ,……, nx .证明: 对一切 *nN , 2 31 0ng g x g x g xx 成立. 【答案】(1)函数 f x 在区间 50, 2 上有两个零点;(2)证明见解析. 【解析】 【分析】 (1)先求出 ( ) cosf x x x ,再对 x 分三个区间:当 0, 2 x , 3 2 2 x , , 3 5, 2 2 x ,讨论单调性,得到 ( )f x 在 50, 2 有 2 个零点; (2)根据(1)中结论可知 1 , 2 x , 2 3 ,2 2 x ,化简 1 2g x g x 为 1 2sin sinx x ,根据 siny x 单调性可证得 1 2 0g x g x ,进而证得 2 1 2 0k kg x g x ,分别在n为奇数和 n为偶数两种情况下,采取分组求和的方式,相邻 两项配对,即可证得结论. - 21 - 【详解】解:(1)∵ cosf x x x , 当 0, 2 x 时, 0f x , ∴ 0f x f ,∴ f x 无零点; 当 3 2 2 x , 时, 0f x , ∴ 0 2 2 f , 3 3 0 2 2 f ,∴ f x 有唯一零点; 当 3 5, 2 2 x 时, 0f x , ∴ 5 5 0 2 2 f ,∴ f x 有唯一零点; 综上,函数 f x 在区间 50, 2 上有两个零点. (2)∵ 2 f x g x x ,由(1)知 g x 在 0, 2 上无极值点; 在 3, 2 2 x 有极小值点,即为 1x ; 在 3 5, 2 2 x 有极大值点,即为 2x ; 而 0 2 2 f , 1 0f , 3 3 0 2 2 f , 2 1 0f , 可知 1 , 2 x , 2 3 ,2 2 x , 同理在 5 ,3 2 有极小值点 3x ,,在 2 1 , 2 n n 有极值点 nx . 由 sin cos 0n n nx x x ,得 1tan n n x x , - 22 - ∵ 1 2x x ,∴ 1 2 1 1 x x , 1 1 2tan tan tanx x x , 而 1 3 ,2 2 x , 2 3 ,2 2 x ,故有 1 2x x , 1 2 1 2 1 2 cos cosx xg x g x x x 1 2sin sinx x 1 2sin sinx x , ∵ siny x 在 3 ,2 2 是增函数, 1 2sin sin 0x x , 即 1 2 0g x g x ; 同理, 2 1 4 3 , 2 1 2k kx k , 2 4 1 ,2 2k kx k , 2 1 2 4 1 2 2 k k k x x k , 由 siny x 在 4 1 ,2 2 k k 递增得 2 1 2 2 1 2sin sin 0k k k kg x g x x x , 当 2n k 时, 1 2 3 4g x g x g x g x 2 1 2 0k kg x g x ,结论成立; 当 2 1n k 时, 2 1 4 1 , 2 1 2k kx k , 2 1 2 1 sin 0k kg x x , 1 2 3 4g x g x g x g x 22 12 1 0k k kg x g x g x ,结论成立; 综上,对一切 *nN , 31 2 0ng x g x g x g x 成立. 【点睛】本题主要考查利用导数研究函数的零点,考查利用导数研究函数的极值点,考查利 用导数证明不等式,意在考查学生对这些知识的理解掌握水平和分析推理能力. - 23 - 21. 计算 的最为稀奇的方法之一,要数 18 世纪法国的博物学家C·蒲丰和他的投针实验: 在一个平面上,用尺画一组相距为 a的平行线,一根长度为 a的针,扔到画了平行线的平面上, 如果针与线相交,则该次扔出被认为是有利的,否则是不利的.如图①,记针的中点为M , 设M 到平行线的最短距离为 y,针与平行线所成角度为 x,容易发现随机情况下满足 0, 2 0, ay x ,且针与线相交时需 sin 2 ay x . (1)数学兴趣小组的同学利用随机模拟的方法,投针实验.记实验次数为 n,其中有利次数为 m . (i)结合图②,利用几何概型计算一次实验结果有利的概率值 0P ; (ii)求出该实验中 的估计值; (2)若投针实验进行了10000次,以 X 表示有利次数,试求 X 的期望(用 表示),并求当 的估计值与实际值误差小于0.01的概率. 附: 10000 10000 0 2 21 i ik i i P k C k 6345 6346 6385 6386 P k 0.3332 0.3408 0.6556 0.6632 参考数值: 1 0.3193 0.01 , 1 0.3173 0.01 . (3)某校数学兴趣小组有30名学生,学校安排周二或周五的第 7节课在数学实验室开展上机 实验.由于数学实验室只有 20台电脑可供使用,周二、周五数学兴趣小组都有 20名学生一人一 机实验,假设学生相互独立地随机上机.设 表示参加周二或周五上机实验的人数,当 为多 少时,其概率最大. - 24 - 【答案】(1)(i) 2 ;(ii) 2n m ;(2)期望: 20000 ,概率为:0.3148;(3)当 为 27 时, 其概率最大. 【解析】 【分析】 (1)(i)根据几何概型面积型可直接求得结果; (ii)利用古典概型概率公式和(i)中结果可构造方程求得估计值; (2)易知 X 服从于二项分布,利用二项分布数学期望计算公式可求得期望;根据 20000 0.01 X 可求得 X 的值,结合所给数据求得概率; (3)当 k 时,可确定其包含的基本事件总数,由古典概型概率公式可得 P k ,根据 1 1 P k P k P k P k ,结合组合数公式可化简求得 k的范围,结合 k N 可得结果. 【详解】(1)(i) 0 sinS xdx a 阴影 , = 2 aS 矩形 , 0 2S P S 阴影 矩形 ; (ii) 2 m n , 2n m ,故该实验中 的估计值为 2n m ; (2) 210000,X B , 2 2000010000E X , 的估计值 2 20000n m X ,由 20000 0.01 X 得: 20000 20000 0.01 0.01 X , 由参考值知:6346 6386X , 故所求概率为 6346 6386 6385 6346 0.3148P X P P . (3)学生随机独立地上机所包含的基本事件总数为 220 30C , 当 k 时,只参加周二上机实验的人数为 20k ,只参加周五上机实验的人数为 20k , 周二、周五都参加上机实验的人数为 40 k . 事件 k 所包含的基本事件总数为 20 40 20 30 20 10 k kC C C , 20 40 20 40 20 30 20 10 20 10 2 2020 3030 k k k kC C C C CP k CC , - 25 - 若 P k 最大,则 1 1 P k P k P k P k , 即 40 140 20 1 20 20 10 20 10 20 20 30 30 40 140 20 1 20 20 10 20 10 20 20 30 30 kk k k kk k k C C C C C C C C C C C C , 20! 10! 20! 10! 40 ! 20 ! 20 ! 30 ! 40 1 ! 1 20 ! 1 20 ! 30 1 ! 20! 10! 20! 10! 40 ! 20 ! 20 ! 30 ! 40 1 ! 1 20 ! 1 20 ! 30 1 ! k k k k k k k k k k k k k k k k , 1 1 1 1 40 30 1 20 1 20 1 1 1 1 20 20 40 1 30 1 k k k k k k k k , 2 2 19 40 30 41 31 20 k k k k k k ,解得: 839 871 32 32 k , 26.2 27.2k , k N Q , 27k . 故当 为 27时,其概率最大. 【点睛】本题考查古典概型和几何概型的应用、二项分布数学期望的求解和应用、概率最大 问题的求解;求解概率最大问题的关键是能够通过 1 1 P k P k P k P k 构造出不等关 系,结合组合数公式求解结果;本题计算量较大,对于学生运算和求解能力有较高要求. 22. 平面直角坐标系 xOy中,直线 l的参数方程为 13 2 31 2 x t y t ( t为参数),以坐标原点为 极点, x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 2sin . (1)求直线 l的极坐标方程及曲线C的直角坐标方程; (2)若 1,A 是直线 l上一点, 2 , 3 B 是曲线C上一点,求 | | | | OB OA 的最大值. - 26 - 【答案】(1) 3 2 0x y , 2 2 2 0x y y ;(2)2. 【解析】 【分析】 (1)消去参数可得普通方程,极坐标与直角坐标互化公式可得答案; (2)根据极坐标的几何意义以及三角函数的最值可得 答案. 【详解】(1)由题,直线 l的参数方程为 13 2 31 2 x t y t (其中 t为参数). 消去参数 t得直线 l的直角坐标方程为 3 2 0x y , 由 cos x , sin y ,得直线 l的极坐标方程 3 cos sin 2 , 即 cos 1 6 曲线C的极坐标方程为 2sin ,所以 2 2 sin , 由 2 2 2x y , sin y ,得曲线C的直角坐标方程为 2 2 2 0x y y . (2)因为 1,A 在直线 l上, 2 , 3 B 在曲线C上, 所以 1 cos 1 6 , 2 2sin 2cos 2cos 3 3 2 6 , 所以 2 2 1 | | 2cos 2 | | 6 OB OA , OB OA 的最大值为 2. 【点睛】本题考查了参数方程化普通方程,考查了极坐标与直角坐标互化公式,考查了极坐标 的几何意义,考查了三角函数的最值,属于中档题. 23. 已知函数 f(x)=|x﹣2|﹣t,t∈R,g(x)=|x+3|. (1)x∈R,有 f(x)≥g(x),求实数 t的取值范围; (2)若不等式 f(x)≤0的解集为[1,3],正数 a、b 满足 ab﹣2a﹣b=2t﹣2,求 a+2b 的最 小值. - 27 - 【答案】(1) , 5 ;(2) min( 2 ) 9a b 【解析】 【分析】 (1)由条件可知,当 x∈R 时, | 2 | | 3 |t x x 恒成立,因此只需 min| 2 | | 3 |t x x ,然后利 用绝对值三角不等式可求出 | 2 | | 3 |x x 的小值即可. (2)根据不等式 f(x)≤0 的解集为[1,3],求出 t的值,然后将 t代入 2 2 2ab a b t 中,得到 关于 a ,b的方程,再利用基本不等式求出 2a b的最小值即可. 【详解】解:(1)因为 x∈R,有 f(x)≥g(x),所以 | 2 | | 3 |x t x 在 x∈R 时恒成立, 即 | 2 | | 3 |t x x 在 x∈R 时恒成立,所以只需 min| 2 | | 3 |t x x 因为 || 2 | | 3 || | 2 3 | 5x x x x ,所以 5 | 2 | | 3 | 5x x , 所以 min| 2 | | 3 | 5t x x , 所以 t 的取值范围为 ( , 5] . (2)由 | 2 |x t ,得 2 2t x t , 因为不等式 ( ) 0f x 的解集为[1, 3] ,所以 2 1 2 3 t t ,解得 1t . 将 1t 带入 2 2 2ab a b t 中,得 2 0ab a b ,所以 2 1 1 b a , 所以 2 1 2 2 2 22 ( 2 )( ) 5 2 5 9a b a ba b a b b a b a b a ,当且仅当 3a b 时取等号, 所以 2a b的最小值为 9. 【点睛】本题考查了不等式恒成立问题、不等式的解集与方程根的关系、绝对值三角不等式 和利用基本不等式求最值,考查了转化思想和方程思想,属中档题. - 28 -查看更多