- 2021-06-16 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
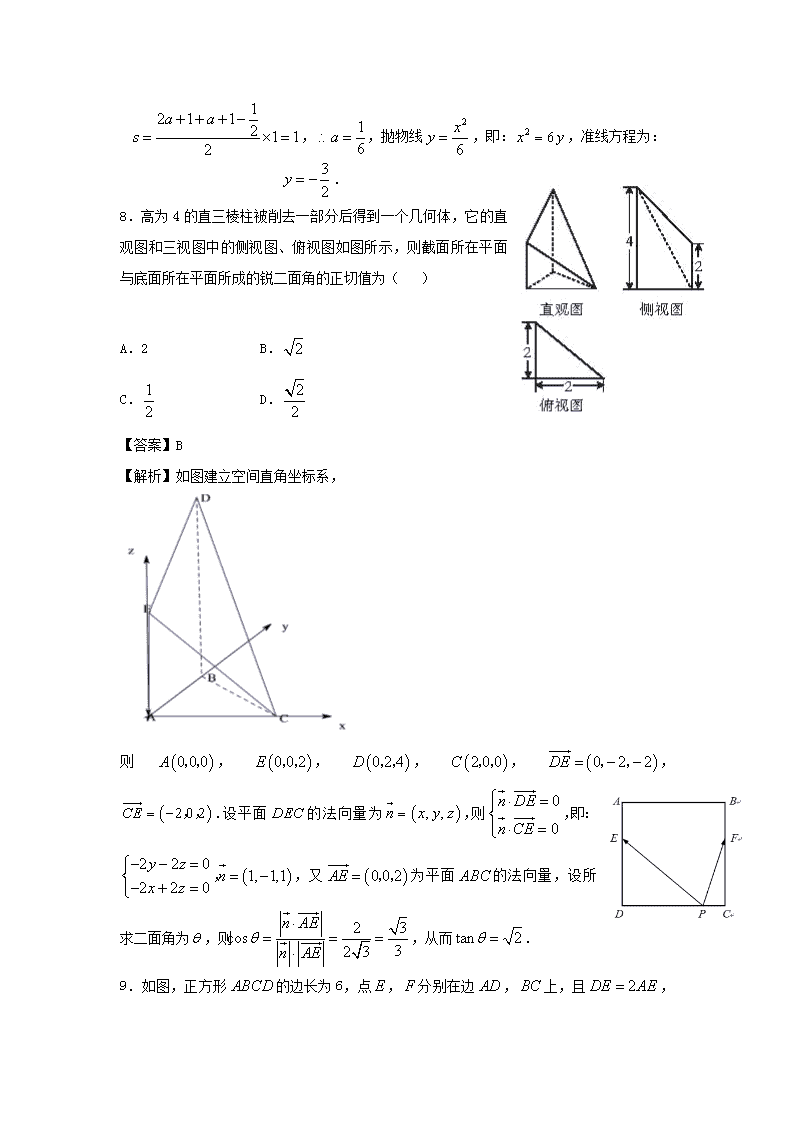
成都外国语学校高二下期入学考试数学试题(理)
成都外国语学校高二下期入学考试数学试题(理) 1.设集合 2 4 0 , 2 0A x x B x x ,则 A B ( ) A. 2x x B. 2x x C. 2x x 或 2x D. 1 2x x 【答案】B 2.已知命题 p: 0,ln 1 0x x ;命题 q:若 a>b,则 a2>b2,下列命题为真命题的 是 A. p q B. p q C. p q D. p q 【 解 析 】 由 0x 时 1 1,ln 1x x 有 意 义 , 知 p 是 真 命 题 , 由 2 22 22 1,2 1 ; 1 2, 1 2 可知 q 是假命题,即 ,p q 均是真命题,故选 B. 3.若 π 1cos( )4 3 , (0, )2 ,则sin 的值为( ) A. 4 2 6 B. 4 2 6 C. 7 18 D. 2 3 【答案】A 4.阅读如图所示的程序框图,若运行相应的程序输出的结果为 0,则判断框中的条件不可 能是( ) A. 2014n≤ B. 2015n≤ C. 2016n≤ D. 2018n≤ 【答案】A 【解析】前 6 步的执行结果如下: 0, 1s n ; 3, 2s n ; 0, 3s n ; 0, 4s n ; 3, 5s n ; 0, 6s n ;观察可知, s 的值以 3 为周期循环出现,所以判断条件为 2014n≤ ?时, 3s 符合题意. 5.函数 20164cos 2016 e xy x ( e 为自然对数的底数)的图像可能是( ) 【解析】由解析式知函数为偶函数,故排除 B、D,又 0 4 1 3 0f ,故选 A. 6.若直线 ax﹣by+2=0(a>0,b>0)被圆 x2+y2+2x﹣4y+1=0 截得的弦长为 4,则 的最 小值为( ) A. B. C. + D. +2 试题分析:圆即(x+1)2+(y﹣2)2=4,表示以 M(﹣1,2)为圆心,以 2 为半径的圆,由 题意可得 圆心在直线 ax﹣by+2=0 上,得到 a+2b=2,故 = + + +1,利用基本不等 式求得式子的最小值. 解:圆 x2+y2+2x﹣4y+1=0 即 (x+1)2+(y﹣2)2=4,表示以 M(﹣1,2)为圆心,以 2 为 半径的圆, 由题意可得 圆心在直线 ax﹣by+2=0(a>0,b>0)上,故﹣1a﹣2b+2=0, 即 a+2b=2,∴ = + = + + +1≥ +2 = , 当且仅当 时,等号成立,故选 C. 7.在平面直角坐标系中,若不等式组 2 2 1 2 1 0 x y x ax y ≥ ≤ ≤ ≥ ( a 为常数)表示的区域面积等于 1, 则抛物线 2y ax 的准线方程为( ) A. 1 24y B. 1 24x C. 3 2x 【答案】D 【解析】作可行域: 由题知: 2,2 1A a , 1, 1B a , 11, 2C , 2,0D , 12 1 1 2 1 12 a a s , 1 6a ,抛物线 2 6 xy ,即: 2 6x y ,准线方程为: 3 2y . 8.高为 4 的直三棱柱被削去一部分后得到一个几何体,它的直 观图和三视图中的侧视图、俯视图如图所示,则截面所在平面与 底面所在平面所成的锐二面角的正切值为( ) A.2 B. 2 C. 1 2 D. 2 2 【答案】B 【解析】如图建立空间直角坐标系, 则 0 0 0A ,, , 0 0 2E ,, , 0 2 4D ,, , 2 0 0C ,, , 0 2 2DE , , , 2 0 2CE ,, .设 平面 DEC 的法向量为 , ,n x y z ,则 0 0 n DE n CE ,即: 2 2 0 2 2 0 y z x z , 1, 1,1n ,又 0 0 2AE ,, 为平面 ABC 的法向量,设所求二面角为 ,则 2 3cos 32 3 n AE n AE ,从而 tan 2 . 9.如图,正方形 ABCD 的边长为 6,点 E , F 分别在边 AD , BC 上,且 2DE AE , 2CF BF .若有 7,16 ,则在正方形的四条边上,使得 PE PF 成 立的点 P 有( )个 A.2 B.4 C.6 D.0 【答案】B 【解析】若 P 在 AB 上, 5,4PE PF PA AE PB BF PA PB AE BF ; 若 P 在CD 上, 7,16PE PF PD DE PC CF PD PC DE CF ; 若 P 在 AE 上, 0,4PE PF PE PA AB BF PE PA PE BF ; 同理, P 在 BF 上时也有 0,4PE PF ; 若 P 在 DE 上, 0,16PE PF PE PD DC CF PE PD PE CF ; 同理, P 在CF 上时也有 0,16PE PF ; 所以,综上可知当 7,16 时,有且只有 4 个不同的点 P 使得 PE PF 成立. 10.已知双曲线 2 2 1x y 的左、右顶点分别为 1 A 、 2 A ,动直线 :l y kx m 与圆 2 2 1x y 相切,且与双曲线左、右两支的交点分别为 1 1 1,P x y , 2 2 2,P x y ,则 2 1x x 的最小值为( ) A. 2 2 B.2 C . 4 D.3 2 【答案】A l 与圆相切, 2 1 1 m k , 2 21m k . 由 2 2 1 y kx m x y ,得 2 2 21 2 1 0k x mkx m , 2 2 2 2 2 2 2 2 1 2 2 1 0 4 4 1 1 4 1 8 0 1 01 k m k k m m k mx x k , 2 1k , 1 1k ,故 k 的取值范围为 1,1 . 由于 1 2 2 2 1 mkx x k , 2 2 1 1 2 1 2 22 2 2 2 24 11 x x x x x x kk , 20 1k ≤ ,当 2 0k 时, 2 1x x 取最小值 2 2 . 11 已知两定点 ( 2,0)A 和 (2,0)B ,动点 ( , )P x y 在直线 : 3l y x 上移动,椭圆 C 以 ,A B 为焦点且经过点 P ,则椭圆C 的离心率的最大值为( ) A. 2 26 B. 4 26 C. 2 13 D. 4 13 12.已知函数 的定义域为 ,当 时, ,且对任意的实数 ,等式 成立,若数列 满足 ,且 ,则下列结论成立 的是( ) A. B. C. D. 【解析】 当 时 与 时, 矛盾,因此 当 时, , 设 ,则 ,因此 为单调减函数,从而 , , , , , 选 D. 13.设 nS 是数列 na 的前 n 项和, 0na ,且 1 36n n nS a a ,则数列 na 的通项公式 为________. 【答案】 3na n 【解析】当 1n 时, 1 1 1 1 1 36S a a a ,解得 1 3a ; 当 2n≥ 时, 1 1 1 1 3 36n n n n n n na S S a a a a , 整理得 1 1 3 0n n n na a a a . 因为 0na ,所以 1 3 0n na a ,即 1 3n na a , 所以 na 是以 3 为首项,3 为公差的等差数列,所以 3 3 1 3na n n ,即 3na n . 14.从某大学随机抽取的 5 名女大学生的身高 x (厘米)和体重 y (公斤)数据如下表; x 165 160 175 155 170 y 58 52 62 43 根据上表可得回归直线方程为 ˆ 0.92 96.8y x ,则表格中空白处的值为________. 【答案】60 【解析】根据回归直线经过样本中心 ,x y 可得,表格中空白处的值为 60. 15.已知点 A 是抛物线 21 4y x 的对称轴与准线的交点,点 F 为该抛物线的焦点,点 P 在 抛物线上且满足 PF m PA ,则 m 的最小值为________. 【答案】 2 2 【解析】如图所示, 0, 1A , 0,1F ,过 P 作准线的垂线,垂足是 H ,由对称性,不妨 令 P 在第一象限, sinPF PHm PAHPA PA , 问题等价于求 PAH 的最小值, 而 21 11 1 1 1 14tan 2 14 4 xyPAH x xx x x x ≥ , 当且仅当 1 1 24 x xx 时等号成立, 所以 2sin 2m PAH ≥ ,即: min 2 2m . 16 过双曲线 的右焦点 作倾斜角为 的直线,交双曲线于 两点,则 的值为___ 解 因为 ,离心率 ,点准距 ,因倾斜角为 ,所以 。注意到 分别在双曲线的两支上,由焦半径公式 得, 。 17.已知函数 23 1sin2 cos2 2f x x x . (1)求 f x 的单调递增区间; (2)设 ABC 的内角 , ,A B C 的对边分别为 , ,a b c ,且 3, 0c f C ,若sin 2sinB A , 求 a b、 的值. 试题解析: (1) 23 1 3 1 2 12 2 2 12 2 2 2 2 6 cos xf x sin x cos x sin x sin x . 由 2 2 2 ,2 6 2k x k k Z ,得 ,6 3k x k k Z ∴函数 f x 的单调递增区间为 ,6 3k k k Z . (2)由 0f C ,得 2 16sin C , 110 , 26 6 6C C , 2 ,6 2 3C C . 又 2sinB sinA ,由正弦定理得 2b a ①; 由余弦定理得 2 2 2 2 3c a b abcos ,即 2 2 3a b ab ,②由①②解得 1, 2a b . 18.为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听 写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根 据甲、乙两人近期 8 次成绩画出茎叶图,如图所示,甲的成绩中 有一个数的个位数字模糊,在茎叶图中用 a 表示.(把频率当作概 率). (1)假设 5a ,现要从甲、乙两人中选派一人参加比赛,从统 计学的角度,你认为派哪位学生参加比较合适? (2)假设数字 a 的取值是随机的,求乙的平均分高于甲的平均分 的概率. 试题解析: (1)由茎叶图可知甲、乙两人成绩的平均数为 1 68 69 71 72 74 78 85 83 758x 甲 , 1 65 70 70 73 75 80 82 85 758x 乙 , ∴ 2 2 2 2 2 2 2 22 1 68 75 69 75 71 75 72 75 74 75 78 75 85 75 83 75 35.58s 甲 2 2 2 2 2 2 2 22 1 65 75 70 75 70 75 73 75 75 75 80 75 82 75 85 75 418s 乙 ∵ x x甲 乙 , 2 2s s甲 乙 , ∴两人的平均成绩相等,但甲的成绩比较稳定,派甲参加比较合适. (2)由 x x甲 乙 ,得 1 60 2 70 4 80 2 8 9 1 2 4 8 3 758 a ,∴ 5a , 又 a 为整数,∴ 0,1,2,3,4a , 又 a 的所有可能取值为 0,1,2,3,4,5,6,7,8,9,∴乙的平均分高于甲的平均分的概率为 1 2 . 19.正项数列 na 满足 2 1 1 2 1 3 1 0n n n n na a a a a , 1 1a ,数列 nb 为等差 数列, 3 21b a , 3 13a b . (1)求证: 1 2na 是等比数列,并求 nb 的通项公式; (2)令 n n nc a b ,求数列 nc 的前 n 项和 nT 试题解析: (1)由题可得 1 1 3 1 0n n n na a a a , ∵ 0na ,∴ 1 3 1n na a ,∴ 1 1 132 2n na a , 又 1 1 3 02 2a ,∴ 数列 1 2na 是首项为 3 2 ,公比为 3 的等比数列. ∴ 11 3 332 2 2 n n na ,∴ 3 1 2 n na .∴ 2 34, 13a a , 由题意得 1 1 2 1 4{ 12 13 b d b d ,解得 1 1,{ 1. b d ∴ 1 1nb n n . (2)由(1)得 3 1 2 n na , nb n ,∴ 1 13 1 32 2 n n nc n n n , ∴ 21 11 3 2 3 3 1 22 2 n nT n n 2 11 1 3 2 3 32 4 n n nn , 令 21 3 2 3 3n nS n ①, 则 2 3 13 1 3 2 3 3n nS n ②, ① ②得 2 12 3 3 3 3n n nS n 1 13 3 32 n nn 11 3( ) 32 2 nn . 所以 11 332 4 4 n n nS .∴ 11 11 1 332 4 4 8 8 4 n n n n n n nnT S 20.如图,在四棱锥 P-ABCD 中,底面 ABCD 为正方形,平面 PAD⊥平面 ABCD,点 M 在线段 PPD//平面 MAC,PA=PD= 6 ,AB=4. (I)求证:M 为 PB 的中点; (II)求二面角 B-PD-A 的大小; (III)求直线 MC 与平面 BDP 所成角的正弦值. 试题解析:解:(I)设 ,AC BD 交点为 E ,连接 ME . 因为 PD 平面 MAC ,平面 MAC 平面 PBD ME ,所以 PD ME . 因为 ABCD 是正方形,所以 E 为 BD 的中点,所以 M 为 PB 的中点. (II)取 AD 的中点O ,连接 OP , OE . 因为 PA PD ,所以OP AD . 又因为平面 PAD 平面 ABCD ,且OP 平面 PAD ,所以 OP 平面 ABCD . 因为OE 平面 ABCD ,所以OP OE . 因为 ABCD 是正方形,所以OE AD . 如图建立空间直角坐标系O xyz ,则 0,0, 2P , 2,0,0D , 2,4,0B , 4, 4,0BD , 2,0, 2PD . 设平面 BDP 的法向量为 , ,n x y z ,则 0{ 0 n BD n PD ,即 4 4 0 { 2 2 0 x y x z . 令 1x ,则 1y , 2z .于是 1,1, 2n . 平面 PAD 的法向量为 0,1,0p ,所以 1cos , 2 n pn p n p . 由题知二面角 B PD A 为锐角,所以它的大小为 3 . (III)由题意知 21,2, 2M , 2,4,0D , 23,2, 2MC . 设直线 MC 与平面 BDP 所成角为 ,则 2 6sin cos , 9 n MC n MC n MC . 所以直线 MC 与平面 BDP 所成角的正弦值为 2 6 9 . 21.已知函数 1 2 1log 1 axf x x 为奇函数, a 为常数. (1)确定 a 的值; (2)求证: f x 是 1 , 上的增函数; (3)若对于区间 3 4, 上的每一个 x 值,不等式 1 2 x f x m 恒成立,求实数 m 的取 值范围. 试题解析: (1)∵函数 f x 是奇函数, f x f x , 即 1 1 2 2 1 1log log1 1 ax ax x x ∴ 1 1 1 1 ax x x ax ,整理 得 2 2 21 1x a x , ∴ 2 1a ,解得 1a , 当 1a 时, 1 11 ax x ,不合题意舍去, ∴ 1a 。 ( 2 ) 由 ( 1 ) 可 得 1 2 1log 1 xf x x , 设 1 2 1 2, 1,x x x x ,且 , 则 2 1 1 2 1 22 1 2 1 2 1 2 1 1 1 1 1 21 1 1 1 1 1 1 1 x x x x x xx x x x x x x x , ∵ 2 1 1x x ,∴ 1 2 2 10,( 1) 1 0,x x x x ∴ 1 2 2 1 2 01 1 x x x x ,∴ 2 1 2 1 1 1 1 1 x x x x , ∴ 2 1 1 1 2 12 2 1 1log log1 1 x x x x ,即 2 1f x f x .∴ f x 是 1 , 上的增函数. (3)依题意得 1 2 1 1log 1 2 xxm x 在 3 4, 上恒成立, 设 1 2 1 1log 1 2 xxu x x , x 3 4 , , 由(2)知函数 1 2 1 1log 1 2 xxu x x 在 3 4, 上单调递增, ∴当 min 9x 3 3 8u x u x u 时, 有最小值,且 ,所以 9 8m . 故实数 m 的取值范围为 9, 8 . 22.如图, O 为坐标原点,椭圆 1 :C 2 2 2 2 1( 0)x y a ba b 的左右焦点分别为 1 2,F F ,离心 率为 1e ;双曲线 2 :C 2 2 2 2 1x y a b 的左右焦点分别为 3 4,F F ,离心率为 2e ,已知 1 2 3 2e e , 且 2 4 3 1F F . (1)求 1 2,C C 的方程; (2)过 1F 点作 1C 的不垂直于 y 轴的弦 AB , M 为 AB 的中点,当直线OM 与 2C 交于 ,P Q 两点时,求四边形 APBQ 面积的最小值. (1) 由 题 可 得 2 2 1 22 21 , 1b be ea a , 且 2 2 1 2 2F F a b , 因 为 1 2 3 2e e , 且 2 2 2 2 2 4F F a b a b , 所 以 2 2 2 2 31 1 2 b b a a 且 2 2 2 2 3 1a b a b 2a b 且 1, 2b a , 所 以 椭 圆 1C 方 程 为 2 2 12 x y ,双曲线 2C 的方程为 2 2 12 x y . (2)由(1)可得 2 1,0F ,因为直线 AB 不垂直于 y 轴,所以设直线 AB 的方程为 1x ny , 联立直线与椭圆方程可得 2 22 2 1 0n y ny ,则 2 2 2A B ny y n , 2 1 2A By y n , 则 2 2m ny n ,因为 ,M MM x y 在直线 AB 上,所以 2 2 2 212 2M nx n n ,则直线 PQ 的方程为 2 M M y ny x y xx ,联立直线 PQ 与双曲线可得 2 2 2 2 02 nx x 2 2 4 2x n , 2 2 22 ny n 则 22 0 2 2n n , 则 2 2 2 2 42 2 2 nPQ x y n ,设点 A 到直线 PQ 的距离为 d ,则 B 到直线 PQ 的距离也 为 d , 则 2 2 2 2 4 A A B Bnx y nx y d n , 因 为 ,A B 在 直 线 PQ 的 两 端 , 所 以 2 2 0B B A Anx y nx y , 则 2 2 2 2 4 A A B Bnx y nx y d n 2 2 2 4 A A B Bnx y nx y n , 又 因 为 ,A B 在 直 线 1x ny 上 , 所 以 2 2 2 2 4 A Bn y y d n 22 2 2 2 2 4 2 2 1 4 4 A B A Bn y y y y n n n , 则 四 边 形 APBQ 面 积 2 22 2 2 1 32 2 1 22 n nn , 因 为 20 2 2n ,所以当 2 0n 时,四边形 APBQ 面积的最小值为 2 .查看更多