【数学】2020届一轮复习人教版（理）第2章第1讲函数及其表示学案

【数学】2020届一轮复习人教版（理）第2章第1讲函数及其表示学案

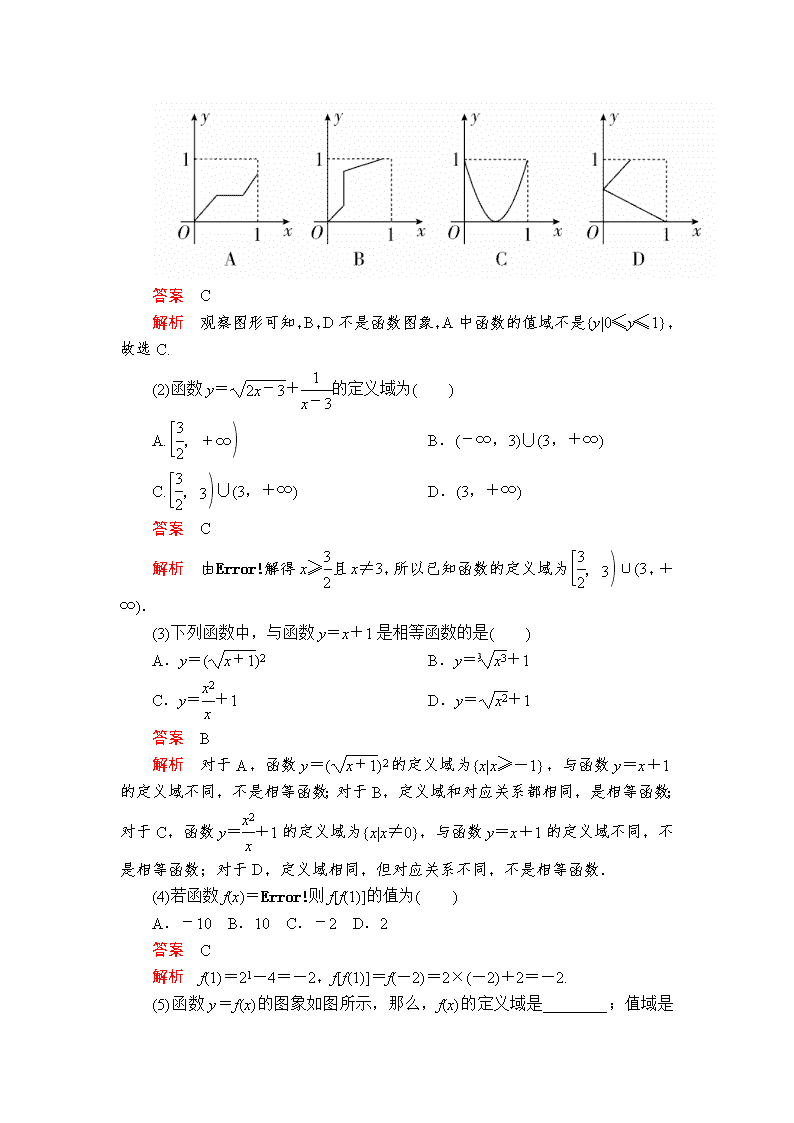
第1讲　函数及其表示 ‎[考纲解读]　1.了解构成函数的要素，会求一些简单函数的定义域和值域；了解映射的概念．(重点)‎ ‎2.在实际情境中，会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数．(重点)‎ ‎3.了解简单的分段函数，并能简单应用(函数分段不超过三段)．(难点)‎ ‎[考向预测]　从近三年高考情况来看，本讲是高考中的一个热点．预测2020年会考查函数的解析式与分段函数的应用，可能涉及函数的求值、函数图象的判断及最值的求解.‎ ‎1．函数与映射 ‎2．函数的有关概念 ‎(1)函数的定义域、值域 在函数y＝f(x)，x∈A中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的值域．‎ ‎(2)函数的三要素：定义域、对应关系和值域．‎ ‎(3)函数的表示法 表示函数的常用方法有解析法、图象法和列表法．‎ ‎3．分段函数 ‎(1)定义：若函数在其定义域内，对于定义域内的不同取值区间，有着不同的对应关系，这样的函数通常叫做分段函数．‎ ‎(2)分段函数的相关结论 ‎①分段函数虽由几个部分组成，但它表示的是一个函数．‎ ‎②分段函数的定义域等于各段函数的定义域的并集，值域等于各段函数的值域的并集．‎ ‎1．概念辨析 ‎(1)对于函数f：A→B，其值域就是集合B.(　　)‎ ‎(2)若两个函数的定义域与值域相同，则这两个函数相等．(　　)‎ ‎(3)A＝{1,4,9}，B＝{－3，－2，－1,1,2,3}．‎ f：x→x的平方根是A到B的映射．(　　)‎ ‎(4)分段函数是一个函数，而不是两个或多个函数．(　　)‎ 答案　(1)×　(2)×　(3)×　(4)√‎ ‎　 　　　　　　　　　　　　　　　　　　‎ ‎2．小题热身 ‎(1)下列图形中可以表示为以M＝{x|0≤x≤1}为定义域，以N＝{y|0≤y≤1}为值域的函数的是(　　)‎ 答案　C 解析　观察图形可知，B，D不是函数图象，A中函数的值域不是{y|0≤y≤1}，故选C.‎ ‎(2)函数y＝＋的定义域为(　　)‎ A. B．(－∞，3)∪(3，＋∞)‎ C.∪(3，＋∞) D．(3，＋∞)‎ 答案　C 解析　由解得x≥且x≠3，所以已知函数的定义域为∪(3，＋∞)．‎ ‎(3)下列函数中，与函数y＝x＋1是相等函数的是(　　)‎ A．y＝()2 B．y＝＋1‎ C．y＝＋1 D．y＝＋1‎ 答案　B 解析　对于A，函数y＝()2的定义域为{x|x≥－1}，与函数y＝x＋1的定义域不同，不是相等函数；对于B，定义域和对应关系都相同，是相等函数；对于C，函数y＝＋1的定义域为{x|x≠0}，与函数y＝x＋1的定义域不同，不是相等函数；对于D，定义域相同，但对应关系不同，不是相等函数．‎ ‎(4)若函数f(x)＝则f[f(1)]的值为(　　)‎ A．－10 B．‎10 C．－2 D．2‎ 答案　C 解析　f(1)＝21－4＝－2，f[f(1)]＝f(－2)＝2×(－2)＋2＝－2.‎ ‎(5)函数y＝f(x)的图象如图所示，那么，f(x)的定义域是________；值域是________；其中只有唯一的x值与之对应的y 值的范围是________．(图中，曲线l与直线m无限接近，但永不相交)‎ 答案　[－3,0]∪[1,4)　[1，＋∞)　[1,2)∪(5，＋∞)‎ 解析　观察函数y＝f(x)的图象可知，f(x)的定义域为[－3,0]∪[1,4)，值域是[1，＋∞)，当y∈[1,2)∪(5，＋∞)时，只有唯一的x值与之对应．‎ 题型 　函数的定义域 ‎1．函数y＝的定义域为(　　)‎ A．(－∞，1] B．[－1,1]‎ C．[1,2)∪(2，＋∞) D.∪ 答案　D 解析　由得－1≤x≤1，且x≠－，所以函数y＝的定义域为∪，故选D.‎ ‎2．函数f(x)的定义域是[2，＋∞)，则函数y＝的定义域是(　　)‎ A．[1，＋∞) B．(－∞，1]‎ C．[1,2)∪(2，＋∞) D．[2，＋∞)‎ 答案　C 解析　依题意，解得x≥1且x≠2，所以函数y＝的定义域是[1,2)∪(2，＋∞)．‎ ‎1．函数y＝f(x)的定义域 ‎2．抽象函数的定义域的求法 ‎(1)若已知函数f(x)的定义域为[a，b]，则复合函数f[g(x)]的定义域由a≤g(x)≤b求出．如举例说明2中f(x)的定义域是[2，＋∞)；f(2x)中x应满足2x≥2.‎ ‎(2)若已知函数f[g(x)]的定义域为[a，b]，则f(x)的定义域为g(x)在x∈[a，b]时的值域．　 　　　　　　　　　　　　　　　　　　‎ ‎1．(2018·潍坊二模)函数f(x)＝＋lg (－3x2＋5x＋2)的定义域为______．‎ 答案　 解析　由得所以－－1)‎ 解析　令t＝－1，则由x>0知－1>－1，x＝，所以由f＝lg x，得f(t)＝lg (t>－1)，所以f(x)＝lg (x>－1)．‎ ‎2．已知f＝x2＋x－2，则f(x)＝________.‎ 答案　x2－2(x≥2或x≤－2)‎ 解析　因为f＝x2＋x－2＝2－2，‎ 且当x>0时，x＋≥2；当x<0时，x＋≤－2，‎ 所以f(x)＝x2－2(x≥2或x≤－2)．‎ ‎3．已知f(x)是二次函数且f(0)＝5，f(x＋1)－f(x)＝x－1，则f(x)＝________.‎ 答案　x2－x＋5‎ 解析　因为f(x)是二次函数且f(0)＝5，‎ 所以设f(x)＝ax2＋bx＋5(a≠0)．‎ 又因为f(x＋1)－f(x)＝x－1，‎ 所以a(x＋1)2＋b(x＋1)＋5－(ax2＋bx＋5)＝x－1，‎ 整理得(‎2a－1)x＋a＋b＋1＝0，所以 解得a＝，b＝－，所以f(x)＝x2－x＋5.‎ ‎4．已知f(x)满足‎2f(x)＋f＝3x，则f(x)＝________.‎ 答案　2x－(x≠0)‎ 解析　因为‎2f(x)＋f＝3x，①‎ 所以将x用替换，得‎2f＋f(x)＝，②‎ 由①②解得f(x)＝2x－(x≠0)，‎ 即f(x)的解析式是f(x)＝2x－(x≠0)．‎ 条件探究1　举例说明2中“x＋”改为“x－”‎ ‎，其他条件不变，该如何求解？‎ 解　因为f＝x2＋x－2＝2＋2，‎ 当x≠0时，x－∈R，所以f(x)＝x2＋2，x∈R.‎ 条件探究2　举例说明4中“f”改为“f(－x)”，其他条件不变，该如何求解？‎ 解　因为‎2f(x)＋f(－x)＝3x，①‎ 所以将x用－x替换，得‎2f(－x)＋f(x)＝－3x，②‎ 由①②解得f(x)＝3x，即f(x)的解析式是f(x)＝3x.‎ 求函数解析式的四种方法 ‎　 　　　　　　　　　　　　　　　　　　‎ ‎1．若函数f(x)是一次函数，且f[f(x)]＝4x＋3，则函数f(x)的解析式为________．‎ 答案　f(x)＝2x＋1或f(x)＝－2x－3‎ 解析　设f(x)＝ax＋b(a≠0)，则f[f(x)]＝af(x)＋b＝a2x＋ab＋b＝4x＋3，∴解得或∴f(x)＝2x＋1或f(x)＝－2x－3.‎ ‎2．已知f()＝x＋1，则函数f(x)的解析式为________．‎ 答案　f(x)＝x2－1(x≥0)‎ 解析　令t＝，则t≥0，x＝t2－2，‎ 由f()＝x＋1可得f(t)＝t2－2＋1＝t2－1.‎ 故函数f(x)的解析式为f(x)＝x2－1(x≥0)．‎ 题型 　分段函数 角度1　求分段函数的函数值 ‎1．(2018·衡水模拟)已知函数f(x)＝ 则f(2017)＝(　　)‎ A．1 B．‎0 C．－1 D．log32‎ 答案　B 解析　由已知得，当x≥0时，f(x＋4)＝－f(x＋2)＝f(x)，所以f(2017)＝f(4×504＋1)＝f(1)＝－f(－1)＝－log31＝0.‎ 角度2　分段函数与方程、不等式的综合问题 ‎2．设函数f(x)＝若f＝4，则实数a＝(　　)‎ A．－ B．－ C．－或－ D．－2或－ 答案　A 解析　因为<1，所以f＝4×＋a＝a＋.‎ 若a＋≥1，即a≥－时，‎2a＋＝4，‎ 即a＋＝2⇒a＝－>－(成立)；‎ 若a＋<1，即a<－时，则‎4a＋＋a＝4，‎ 即a＝－>－(舍去)，综上a＝－.‎ ‎3．设函数f(x)＝则使得f(x)≤3成立的x的取值范围是________．‎ 答案　(－∞，27]‎ 解析　当x<8时，2ex－8<2<3，此时f(x)≤3恒成立；当x≥8时，由x≤3得x ‎≤27，此时x的取值范围为8≤x≤27.综上所述，x的取值范围为(－∞，27]．‎ ‎1．求分段函数的函数值 ‎(1)基本步骤 ‎①确定要求值的自变量属于哪一区间．‎ ‎②代入该区间对应的解析式求值．‎ ‎(2)两种特殊情况 ‎①当出现f[f(a)]的形式时，应从内到外依次求值．如举例说明2.‎ ‎②当自变量的值所在区间不确定时，要分类讨论，分类标准应参照分段函数不同段的端点．如举例说明2，求f后再求f要分类讨论．‎ ‎2．求分段函数的参数或自变量的值(或范围)的方法 求某条件下参数或自变量的值(或范围)，先假设所求的值或范围在分段函数定义区间的各段上，然后求出相应自变量的值或范围，切记代入检验，看所求的自变量的值或范围是否满足相应各段自变量的取值范围．　 　　　　　　　　　　　　　　　　　　‎ ‎1．(2018·河南郑州三模)设函数f(x)＝ 则f[f(－4)]＝________.‎ 答案　－1‎ 解析　f[f(－4)]＝f(16－4－2)＝f(10)＝－1.‎ ‎2．函数f(x)＝若f(a)≤a，则实数a的取值范围是______．‎ 答案　[－1，＋∞)‎ 解析　当a≥0时，由f(a)＝a－1≤a，解得a≥－2，所以a≥0；当a<0时，由f(a)＝≤a，解得－1≤a≤1，所以－1≤a<0.综上所述，实数a的取值范围是[－1，＋∞)．‎