- 2021-06-16 发布 |
- 37.5 KB |
- 44页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江省2021届高考数学一轮复习第五章三角函数解三角形第6节三角函数的图象与性质课件
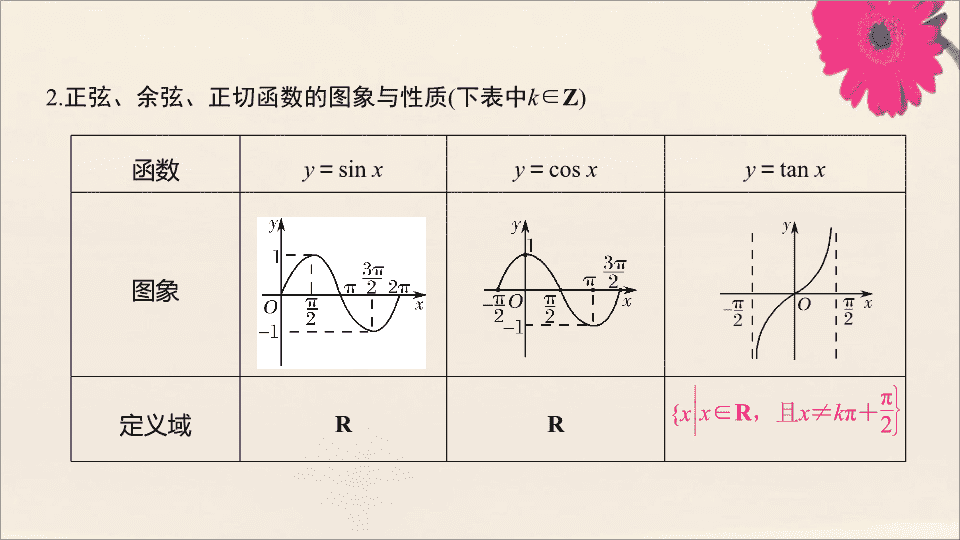
第 6 节 三角函数的图象与性质 知 识 梳 理 (π ,- 1) 2 . 正弦、余弦、正切函数的图象与性质 ( 下表中 k ∈ Z ) 函数 y = sin x y = cos x y = tan x 图象 定义域 R R 值域 R 周期性 2π 奇偶性 奇函数 递增区间 递减区间 无 [2 k π , 2 k π + π] [ - 1 , 1] [ - 1 , 1] 2π π 奇函数 偶函数 [2 k π - π , 2 k π] ( k π , 0) x = k π 诊 断 自 测 1. 判断下列说法的正误 . 解析 (1) 函数 y = sin x 的周期是 2 k π( k ∈ Z ). (2) 余弦函数 y = cos x 的对称轴有无穷多条, y 轴只是其中的一条 . (4) 当 k >0 时, y max = k + 1 ;当 k <0 时, y max =- k + 1. 答案 (1) × (2) × (3) × (4) × (5) √ 答案 D 3. (2018· 全国 Ⅰ 卷 ) 已知函数 f ( x ) = 2cos 2 x - sin 2 x + 2 ,则 ( ) A. f ( x ) 的最小正周期为 π ,最大值为 3 B. f ( x ) 的最小正周期为π,最大值为 4 C. f ( x ) 的最小正周期为 2π ,最大值为 3 D. f ( x ) 的最小正周期为 2π ,最大值为 4 答案 B 答案 C 考点一 三角函数的定义域及三角不等式 规律方法 (1) 三角函数定义域的求法 ① 以正切函数为例,应用正切函数 y = tan x 的定义域求函数 y = A tan( ωx + φ ) 的定义域 . ② 转化为求解简单的三角不等式求复杂函数的定义域 . (2) 简单三角不等式的解法 ① 利用三角函数线求解 . ② 利用三角函数的图象求解 . (2) 法一 要使函数有意义,必须使 sin x - cos x ≥ 0. 利用图象,在同一坐标系中画出 [0 , 2π] 上 y = sin x 和 y = cos x 的图象,如图所示 . 法二 利用三角函数线,画出满足条件的终边范围 ( 如图阴影部分所示 ). 考点二 三角函数的值域 规律方法 求解三角函数的值域 ( 最值 ) 常见到以下几种类型 : (1) 形如 y = a sin x + b cos x + c 的三角函数化为 y = A sin( ωx + φ ) + c 的形式,再求值域 ( 最值 ) ; (2) 形如 y = a sin 2 x + b sin x + c 的三角函数,可先设 sin x = t ,化为关于 t 的二次函数求值域 ( 最值 ) ; (3) 形如 y = a sin x cos x + b (sin x ±cos x ) + c 的三角函数,可先设 t = sin x ±cos x ,化为关于 t 的二次函数求值域 ( 最值 ). =- cos 2 x - 3cos x =- 2cos 2 x - 3cos x + 1 答案 (1)A (2) - 4 (3)B 考点三 三角函数的性质 角度 1 三角函数的奇偶性与周期性 多维探究 规律方法 (1) 求较为复杂的三角函数的单调区间时,首先化简成 y = A sin( ωx + φ ) 形式,再求 y = A sin( ωx + φ ) 的单调区间,只需把 ωx + φ 看作一个整体代入 y = sin x 的相应单调区间内即可,注意要先把 ω 化为正数 .(2) 对于已知函数的单调区间的某一部分确定参数 ω 的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子集,其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解,另外,若是选择题利用特值验证排除法求解更为简捷 .查看更多