【数学】2020届江苏一轮复习通用版17空间向量与立体几何作业
专题十七 空间向量与立体几何
挖命题
【真题典例】
【考情探究】
考点
内容解读
5年考情
预测热度
考题示例
考向
关联考点
空间向量及应用
1.空间向量的概念
2.空间向量共线、共面的充分必要条件
3.空间向量的加法、减法及数乘运算
4.空间向量的坐标表示
5.空间向量的数量积
6.空间向量的共线与垂直
7.空间向量的应用
2015江苏,22
1.求二面角
2.求异面直线所成角
3.空间向量的数量积
直线与平面所成角
★★★
2017江苏,22
1.求异面直线所成角
2.求二面角
3.空间向量的数量积
2018江苏,22
1.求异面直线所成角
2.求直线与平面所成角
3.空间向量的数量积
分析解读 空间向量及其应用在高考中的考查比较单一,主要涉及用空间向量求解空间几何体中的异面直线所成角、直线与平面所成角、二面角以及存在性问题或角的取值范围问题.考查的几何体主要是棱柱、棱锥等常规几何体,难度中等.
破考点
【考点集训】
考点一 空间向量的运算
1.已知a=(λ+1,0,2),b=(6,2μ-1,2λ),若a∥b,则λ与μ的值是 .
答案 2,12或-3,12
2.已知a=(1-t,1-t,t),b=(2,t,t),则|b-a|的最小值为 .
答案 355
3.如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点,计算:
(1)EF·BA;
(2)EF·DC.
解析 设AB=a,AC=b,AD=c,
则|a|=|b|=|c|=1,
===60°.
EF=12BD=12c-12a,BA=-a,DC=b-c,所以
(1)EF·BA=12c-12a·(-a)=12a2-12a·c=14.
(2)EF·DC=12(c-a)·(b-c)=12(b·c-a·b-c2+a·c)=-14.
考点二 空间向量的应用
1.(2018江苏泰兴中学调研,22)如图,在三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连接CD.
(1)若PA=2a,求异面直线PA与CD所成角的余弦值的大小;
(2)若二面角A-PB-C的余弦值的大小为55,求PA.
解析 连接OC.
因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PO⊥AB,PO⊂平面PAB,所以PO⊥平面ABC,从而PO⊥AB,PO⊥OC.
因为AC=BC,点O是AB的中点,所以OC⊥AB,且OA=OB=OC=2a.
如图,建立空间直角坐标系O-xyz.
(1)因为PA=2a,所以PO=PA2-AO2=(2a)2-(2a)2=2a.
所以A(0,-2a,0),B(0,2a,0),C(2a,0,0),P(0,0,2a),D0,2a2,2a2.
从而PA=(0,-2a,-2a),CD=-2a,22a,22a.
因为cos=PA·CD|PA||CD|=-2a22a·3a=-33,所以异面直线PA与CD所成角的余弦值的大小为33.
(2)设PO=h,则P(0,0,h).
因为PO⊥OC,OC⊥AB,而PO∩AB=O,所以OC⊥平面PAB.
从而OC=(2a,0,0)是平面PAB的一个法向量.
不妨设平面PBC的法向量为n=(x,y,z).
因为PB=(0,2a,-h),BC=(2a,-2a,0),所以n·PB=0,n·BC=0,所以2ay=hz,x=y.
不妨令x=1,则y=1,z=2ah,则n=1,1,2ah.
由已知,得55=|OC·n||OC||n|=2a2a·2+2a2h2,
化简得h2=23a2,
所以PA=PO2+OA2=23a2+2a2=263a.
2.(2019届江苏梁丰中学调研)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=2,AF=1.
(1)求二面角A-DF-B的大小;
(2)试在线段AC上确定一点P,使PF与BC所成的角为60°.
解析 (1)由已知易得CD,CB,CE两两垂直,以CD,CB,CE为正交基底建立如图所示的空间直角坐标系C-xyz,则C(0,0,0),D(2,0,0),B(0,2,0),A(2,2,0),E(0,0,1),F(2,2,1).
由题意易得平面ADF的一个法向量为m=(1,0,0).
设平面BDF的法向量为n=(x,y,z).
又BD=(2,-2,0),BF=(2,0,1),
则n·BD=2x-2y=0,n·BF=2x+z=0.
令x=1,则y=1,z=-2,所以n=(1,1,-2)是平面BDF的一个法向量.
设二面角A-DF-B的大小为θ,显然θ为锐角,
所以cos θ=|cos|=(1,0,0)·(1,1,-2)1×2=12,所以θ=60°,即二面角A-DF-B的大小为60°.
(2)设P(λ,λ,0),λ∈[0,2],则PF=(2-λ,2-λ,1),
因为异面直线PF与BC所成的角为60°,所以|cos|=12,
即|-2(2-λ)|2(2-λ)2+1·2=12,解得λ=22或λ=322(舍去).
所以当P是线段AC的中点时,PF与BC所成的角为60°.
3.(2019届江苏高邮中学调研)如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.
(1)求BC与平面EAC所成角的正弦值;
(2)求证:线段ED上不存在点Q,使得平面EAC⊥平面QBC.
解析 (1)因为四边形CDEF为正方形,所以ED⊥DC.
又因为平面CDEF⊥平面ABCD,平面CDEF∩平面ABCD=DC,ED⊂平面CDEF,所以ED⊥平面ABCD.
在平面ABCD内过点D作DH⊥AB,垂足为H,所以ED⊥DH.
因为AB∥CD,所以DH⊥DC.
所以DH,DC,DE两两垂直.
以D为原点,DH,DC,DE所在直线分别为x,y,z轴建立空间直角坐标系D-xyz.
设BC=2,则DC=DE=2,
因为AB=2BC,∠ABC=60°,所以AH=1,HB=3,DH=3,
所以A(3,-1,0),B(3,3,0),C(0,2,0),E(0,0,2),
所以CA=(3,-3,0),CE=(0,-2,2),CB=(3,1,0).
设平面EAC的法向量为n=(x,y,z),则有n·CE=0,n·CA=0.所以-2y+2z=0,3x-3y=0.取z=1,得n=(3,1,1).
设BC与平面EAC所成的角为θ,则sin θ=|cos|=|CB·n||CB||n|=255,
所以BC与平面EAC所成角的正弦值为255.
(2)证明:假设线段ED上存在点Q,设Q(0,0,t)(0≤t≤2),所以CQ=(0,-2,t).
设平面QBC的法向量为m=(a,b,c),则有m·CB=0,m·CQ=0.所以3a+b=0,-2b+tc=0.
取c=2,得m=-t3,t,2是平面QBC的一个法向量.
要使平面EAC⊥平面QBC,只需m·n=0,即-t3×3+t×1+2×1=0,此方程无解.
所以线段ED上不存在点Q,使得平面EAC⊥平面QBC.
炼技法
【方法集训】
方法一 用空间向量求解空间角的方法
1.(2017江苏苏锡常镇四市调研(一))如图,已知正四棱锥P-ABCD中,PA=AB=2,点M,N分别在PA,BD上,且PMPA=BNBD=13.
(1)求异面直线MN与PC所成角的大小;
(2)求二面角N-PC-B的余弦值.
解析 (1)设AC,BD交于点O,连接OP.在正四棱锥P-ABCD中,易得OP⊥平面ABCD.又PA=AB=2,所以OP=2.以O为坐标原点,DA,AB方向分别为x轴、y轴正方向,建立空间直角坐标系O-xyz,如图.
则A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),P(0,0,2),AP=(-1,1,2).
故OM=OA+AM=OA+23AP=13,-13,223,ON=13OB=13,13,0,
所以MN=0,23,-223,又PC=(-1,1,-2),
所以cos=MN·PC|MN||PC|=32,
所以异面直线MN与PC所成角的大小为π6.
(2)由(1)知PC=(-1,1,-2),CB=(2,0,0),NC=-43,23,0.
设m=(x,y,z)是平面PCB的法向量,则m·PC=0,m·CB=0,
即-x+y-2z=0,2x=0,令y=2,则z=1,即m=(0,2,1)是平面PCB的一个法向量.
设n=(x1,y1,z1)是平面PCN的法向量,则n·PC=0,n·NC=0,
即-x1+y1-2z1=0,-2x1+y1=0,令x1=2,则y1=4,z1=2,即n=(2,4,2),
所以cos=m·n|m||n|=523×22=53333,
易知二面角N-PC-B的平面角为锐角,所以二面角N-PC-B的余弦值为53333.
2.(2018江苏扬州中学调研)如图,在直三棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,M是棱BC的中点,点P在线段A1B上.
(1)若P是线段A1B的中点,求直线MP与直线AC所成角的大小;
(2)若N是CC1的中点,直线A1B与平面PMN所成角的正弦值为77,求线段BP的长度.
解析 建立如图所示的空间直角坐标系A-xyz.
则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,2),M(1,1,0).
(1)因为P是线段A1B的中点,
所以P(1,0,1),则MP=(0,-1,1),又AC=(0,2,0).
所以cos=MP·AC|MP|·|AC|=-22.
又∈[0,π],所以=3π4.
所以直线MP与直线AC所成的角的大小为π4.
(2)易得N(0,2,1),所以MN=(-1,1,1).
设P(x,y,z),BP=λBA1,0≤λ≤1,
则(x-2,y,z)=λ(-2,0,2),
所以x=2-2λ,y=0,z=2λ,
所以P(2-2λ,0,2λ),
所以MP=(1-2λ,-1,2λ).
设平面PMN的法向量n=(x,y,z),
则n⊥MN,n⊥MP,
所以-x+y+z=0,(1-2λ)x-y+2λz=0,
取n=1+12λ,12λ,1.
因为BA1=(-2,0,2),设直线A1B与平面PMN所成角为θ.
由sin θ=|cos|=|n·BA1||n|·|BA1|=(-2)×1+12λ+21+12λ2+12λ2+1·22=77,得λ=14(负值舍去).
所以BP=14BA1,所以BP=14BA1=22.
3.(2017江苏镇江期末)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,E是棱PC的中点.
(1)求直线BE与平面PBD所成角的正弦值;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的正弦值.
解析 (1)以A为原点,分别以AB、AD、AP所在直线为x轴、y轴、z轴建立空间直角坐标系A-xyz,
则B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),
由E为棱PC中点,得E(1,1,1),
故BE=(0,1,1),BD=(-1,2,0),PB=(1,0,-2).
设n=(x,y,z)为平面PBD的法向量,
则n⊥BD,n⊥PB,
即-x+2y=0,x-2z=0,不妨令y=1,可得n=(2,1,1)为平面PBD的一个法向量,
于是cos=n·BE|n||BE|=26×2=33.
所以直线BE与平面PBD所成角的正弦值为33.
(2)BC=(1,2,0),CP=(-2,-2,2),AC=(2,2,0),AB=(1,0,0).
由点F在棱PC上,设CF=λCP,0≤λ≤1.
故BF=BC+CF=BC+λCP=(1-2λ,2-2λ,2λ),
由BF⊥AC,得BF·AC=0,
因此2(1-2λ)+2(2-2λ)=0,
解得λ=34,
即BF=-12,12,32.
设n1=(x,y,z)为平面FAB的法向量,
则n1·AB=0,n1·BF=0,
即x=0,-12x+12y+32z=0,
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
取平面ABP的法向量n2=(0,1,0),
则cos=n1·n2|n1||n2|=-31010,
即sin=1010.
故二面角F-AB-P的正弦值为1010.
方法二 利用空间向量求解探索性问题的方法
(2018江苏无锡期末)如图,在四棱锥P-ABCD中,△ABP是等边三角形,底面ABCD是直角梯形,∠DAB=90°,AD∥BC,E是线段AB的中点,PE⊥底面ABCD,已知DA=AB=2BC=2.
(1)求二面角P-CD-A的正弦值;
(2)试在平面PCD上找一点M,使得EM⊥平面PCD.
解析 (1)因为PE⊥底面ABCD,过E作ES∥BC,S为ES与CD的交点,则ES⊥AB,以E为坐标原点,EB方向为x轴的正半轴,ES方向为y轴的正半轴,EP方向为z轴的正半轴建立空间直角坐标系,则E(0,0,0),B(1,0,0),C(1,1,0),A(-1,0,0),D(-1,2,0),P(0,0,3),
故CD=(-2,1,0),PC=(1,1,-3).
设平面PCD的法向量为n=(x,y,z),
则n·CD=-2x+y=0,n·PC=x+y-3z=0.
令x=1,得n=(1,2,3)为平面PCD的一个法向量.
又平面ABCD的一个法向量为m=(0,0,1),
所以cos=n·m|n||m|=31+4+3=64,
所以sin=104,
即所求二面角P-CD-A的正弦值为104.
(2)设点M的坐标为(x1,y1,z1),
因为EM⊥平面PCD,
所以EM∥n,即x11=y12=z13,
也即y1=2x1,z1=3x1.
又PM=(x1,y1,z1-3),PD=(-1,2,-3),PC=(1,1,-3),
所以PM=λPC+μPD=(λ-μ,λ+2μ,-3λ-3μ),
所以x1=λ-μ,y1=λ+2μ=2x1=2(λ-μ),即λ=4μ.
又z1-3=-3λ-3μ,
解得λ=12,所以μ=18,
所以点M的坐标为38,34,338.
过专题
【五年高考】
A组 自主命题·江苏卷题组
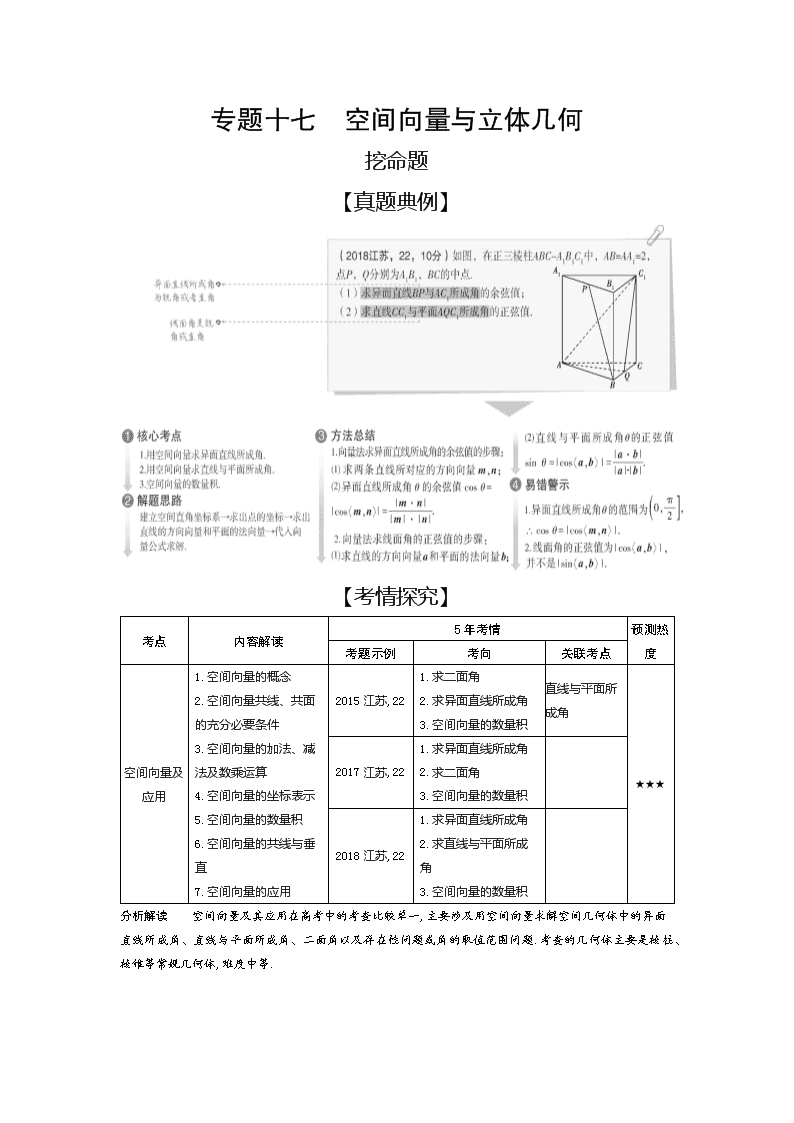
1.(2018江苏,22,10分)如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
解析 本题主要考查空间向量、异面直线所成角和线面角等基础知识,考查运用空间向量解决问题的能力.
如图,在正三棱柱ABC-A1B1C1中,
设AC,A1C1的中点分别为O,O1,
则OB⊥OC,OO1⊥OC,OO1⊥OB,
以{OB,OC,OO1}为基底,建立空间直角坐标系O-xyz.
因为AB=AA1=2,所以A(0,-1,0),B(3,0,0),C(0,1,0),A1(0,-1,2),B1(3,0,2),C1(0,1,2).
(1)因为P为A1B1的中点,所以P32,-12,2.
从而BP=-32,-12,2,AC1=(0,2,2).
故|cos|=|BP·AC1||BP|·|AC1|=|-1+4|5×22=31020.
因此,异面直线BP与AC1所成角的余弦值为31020.
(2)因为Q为BC的中点,所以Q32,12,0,
因此AQ=32,32,0,AC1=(0,2,2),CC1=(0,0,2).
设n=(x,y,z)为平面AQC1的一个法向量,
则 AQ·n=0,AC1·n=0,即32x+32y=0,2y+2z=0.
不妨取n=(3,-1,1).
设直线CC1与平面AQC1所成角为θ,
则sin θ=|cos|=|CC1·n||CC1|·|n|=25×2=55,
所以直线CC1与平面AQC1所成角的正弦值为55.
2.(2017江苏,22,10分)如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=3,∠BAD=120°.
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
解析 在平面ABCD内,过点A作AE⊥AD,交BC于点E.
因为AA1⊥平面ABCD,
所以AA1⊥AE,AA1⊥AD.
如图,以{AE,AD,AA1}为正交基底建立空间直角坐标系A-xyz.
因为AB=AD=2,AA1=3,∠BAD=120°,
则A(0,0,0),B(3,-1,0),D(0,2,0),E(3,0,0),A1(0,0,3),C1(3,1,3).
(1)A1B=(3,-1,-3),AC1=(3,1,3),
则cos=A1B·AC1|A1B||AC1|
=(3,-1,-3)·(3,1,3)7
=-17,
因此异面直线A1B与AC1所成角的余弦值为17.
(2)平面A1DA的一个法向量为AE=(3,0,0).
设m=(x,y,z)为平面BA1D的法向量,
又A1B=(3,-1,-3),BD=(-3,3,0),
则m·A1B=0,m·BD=0,
即3x-y-3z=0,-3x+3y=0.
不妨取x=3,则y=3,z=2,
所以m=(3,3,2)为平面BA1D的一个法向量,
从而cos=AE·m|AE||m|=(3,0,0)·(3,3,2)3×4=34.
设二面角B-A1D-A的大小为θ,则|cos θ|=34.
因为θ∈[0,π],所以sin θ=1-cos2θ=74.
因此二面角B-A1D-A的正弦值为74.
3.(2015江苏,22,10分)如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=π2,PA=AD=2,AB=BC=1.
(1)求平面PAB与平面PCD所成二面角的余弦值;
(2)点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.
解析 以{AB,AD,AP}为正交基底建立如图所示的空间直角坐标系A-xyz,则各点的坐标为B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).
(1)易知AD⊥平面PAB,所以AD是平面PAB的一个法向量,AD=(0,2,0).
因为PC=(1,1,-2),PD=(0,2,-2),
设平面PCD的法向量为m=(x,y,z),
则m·PC=0,m·PD=0,
即x+y-2z=0,2y-2z=0.
令y=1,解得z=1,x=1.
所以m=(1,1,1)是平面PCD的一个法向量.
从而cos=AD·m|AD||m|=33,
所以平面PAB与平面PCD所成二面角的余弦值为33.
(2)因为BP=(-1,0,2),
设BQ=λBP=(-λ,0,2λ)(0≤λ≤1),
又CB=(0,-1,0),
则CQ=CB+BQ=(-λ,-1,2λ),
又DP=(0,-2,2),
从而cos=CQ·DP|CQ||DP|=1+2λ10λ2+2.
设1+2λ=t,t∈[1,3],
则cos2 =2t25t2-10t+9=291t-592+209≤910.
当且仅当t=95,即λ=25时,|cos|的最大值为31010.
因为y=cos x在0,π2上是减函数,所以此时直线CQ与DP所成的角取得最小值.
又因为BP=12+22=5,
所以BQ=25BP=255.
B组 统一命题、省(区、市)卷题组
考点一 空间向量的运算
1.(2017北京理,16,14分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=6,AB=4.
(1)求证:M为PB的中点;
(2)求二面角B-PD-A的大小;
(3)求直线MC与平面BDP所成角的正弦值.
解析 (1)证明:设AC,BD交点为E,连接ME.
因为PD∥平面MAC,平面MAC∩平面PDB=ME,
所以PD∥ME.
因为ABCD是正方形,所以E为BD的中点.
所以M为PB的中点.
(2)取AD的中点O,连接OP,OE.
因为PA=PD,所以OP⊥AD.
又因为平面PAD⊥平面ABCD,且OP⊂平面PAD,
所以OP⊥平面ABCD.
因为OE⊂平面ABCD,所以OP⊥OE.
因为ABCD是正方形,所以OE⊥AD.
如图建立空间直角坐标系O-xyz,则P(0,0,2),D(2,0,0),B(-2,4,0),BD=(4,-4,0),PD=(2,0,-2).
设平面BDP的法向量为n=(x,y,z),
则n·BD=0,n·PD=0,即4x-4y=0,2x-2z=0.
令x=1,则y=1,z=2.
于是n=(1,1,2).
平面PAD的一个法向量为p=(0,1,0).
所以cos=n·p|n||p|=12.
由题意知二面角B-PD-A为锐角,所以它的大小为π3.
(3)由题意知M-1,2,22,C(2,4,0),MC=3,2,-22.
设直线MC与平面BDP所成角为α,
则sin α=|cos|=|n·MC||n||MC|=269.
所以直线MC与平面BDP所成角的正弦值为269.
方法总结 1.在求二面角时,通常用空间向量法,即建立空间直角坐标系,求出两个面的法向量n1,n2,设二面角的大小为θ,则有|cos θ|=|cos|=|n1·n2||n1||n2|,再通过原图判断二面角是钝角还是锐角,进而求出二面角.2.用向量法求直线与平面所成的角的方法:设直线的方向向量为e,平面的法向量为n,则直线与平面所成的角θ满足sin θ=e·n|e||n|,θ∈0,π2.
2.(2018课标全国Ⅱ理,20,12分)如图,在三棱锥P-ABC中,AB=BC=22,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
解析 (1)证明:因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=23.
连接OB.因为AB=BC=22AC,所以△ABC为等腰直角三角形,且OB⊥AC,OB=12AC=2.
由OP2+OB2=PB2知PO⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)如图,以O为坐标原点,OB的方向为x轴正方向,建立空间直角坐标系O-xyz.
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,23),AP=(0,2,23).取平面PAC的一个法向量OB=(2,0,0).
设M(a,2-a,0)(0=23(a-4)23(a-4)2+3a2+a2.
由已知可得|cos|=32.
所以23|a-4|23(a-4)2+3a2+a2=32.解得a=-4(舍去)或a=43.
所以n=-833,433,-43.
又PC=(0,2,-23),所以cos=34.
所以PC与平面PAM所成角的正弦值为34.
考点二 空间向量的应用
1.(2018天津理,17,13分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.
(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;
(2)求二面角E-BC-F的正弦值;
(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.
解析 本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.
依题意,可以建立以D为原点,分别以DA,DC,DG的方向为x轴,y轴,z轴的正方向的空间直角坐标系(如图),可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M0,32,1,N(1,0,2).
(1)证明:依题意DC=(0,2,0),DE=(2,0,2).
设n0=(x0,y0,z0)为平面CDE的法向量,
则n0·DC=0,n0·DE=0,即2y0=0,2x0+2z0=0,
不妨令z0=-1,可得n0=(1,0,-1).
又MN=1,-32,1,可得MN·n0=0,
又因为直线MN⊄平面CDE,
所以MN∥平面CDE.
(2)依题意,可得BC=(-1,0,0),BE=(1,-2,2),CF=(0,-1,2).
设n=(x1,y1,z1)为平面BCE的法向量,
则n·BC=0,n·BE=0,即-x1=0,x1-2y1+2z1=0,
不妨令z1=1,可得n=(0,1,1).
设m=(x2,y2,z2)为平面BCF的法向量,
则m·BC=0,m·CF=0,即-x2=0,-y2+2z2=0,
不妨令z2=1,可得m=(0,2,1).
因此有cos=m·n|m||n|=31010,于是sin=1010.
所以,二面角E-BC-F的正弦值为1010.
(3)设线段DP的长为h(h∈[0,2]),则点P的坐标为(0,0,h),可得BP=(-1,-2,h).
易知,DC=(0,2,0)为平面ADGE的一个法向量,
故|cos|=|BP·DC||BP||DC|=2h2+5.
由题意,可得2h2+5=sin 60°=32,解得h=33∈[0,2].
所以,线段DP的长为33.
方法归纳 利用空间向量解决立体几何问题的一般步骤:
(1)审清题意并建系.利用条件分析问题,建立恰当的空间直角坐标系;
(2)确定相关点的坐标.结合建系过程与图形,准确地写出相关点的坐标;
(3)确定直线的方向向量和平面的法向量.利用点的坐标求出相关直线的方向向量和平面的法向量,若已知某直线垂直某平面,可直接取该直线的方向向量为该平面的法向量;
(4)转化为向量运算.将空间位置关系转化为向量关系,空间角转化为向量的夹角问题去论证、求解;
(5)问题还原.结合条件与图形,作出结论(注意角的范围).
2.(2017浙江,19,15分)如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(1)证明:CE∥平面PAB;
(2)求直线CE与平面PBC所成角的正弦值.
解析 (1)证明:设AD的中点为O,连接OB,OP.
∵△PAD是以AD为斜边的等腰直角三角形,∴OP⊥AD.
∵BC=12AD=OD,且BC∥OD,
∴四边形BCDO为平行四边形,
又∵CD⊥AD,
∴OB⊥AD,∵OP∩OB=O,
∴AD⊥平面OPB.
过点O在平面POB内作OB的垂线OM,交PB于M,
以O为原点,OB所在直线为x轴,OD所在直线为y轴,OM所在直线为z轴,建立空间直角坐标系,如图.
设CD=1,则有A(0,-1,0),B(1,0,0),C(1,1,0),D(0,1,0).
设P(x,0,z)(z>0),由PC=2,OP=1,
得(x-1)2+1+z2=4,x2+z2=1,得x=-12,z=32.
即点P-12,0,32,而E为PD的中点,
∴E-14,12,34.
设平面PAB的法向量为n=(x1,y1,z1),
∵AP=-12,1,32,AB=(1,1,0),
∴-12x1+y1+32z1=0,x1+y1=0⇒x1=-y1,z1=-3y1,
取y1=-1,得n=(1,-1,3).
而CE=-54,-12,34,
则CE·n=0,而CE⊄平面PAB,
∴CE∥平面PAB.
(2)设平面PBC的法向量为m=(x2,y2,z2),
∵BC=(0,1,0),BP=-32,0,32,
∴y2=0,-32x2+32z2=0,取x2=1,得m=(1,0,3).
设直线CE与平面PBC所成角为θ.
则sin θ=|cos|=|CE·m||CE|·|m|=28,
故直线CE与平面PBC所成角的正弦值为28.
一题多解 (1)证明:如图,设PA中点为F,连接EF,FB.因为E,F分别为PD,PA中点,所以EF∥AD且EF=12AD.
又因为BC∥AD,BC=12AD,所以EF∥BC且EF=BC,
即四边形BCEF为平行四边形,所以CE∥BF,
因此CE∥平面PAB.
(2)分别取BC,AD的中点为M,N.
连接PN交EF于点Q,连接MQ.
因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,
在平行四边形BCEF中,MQ∥CE.
由△PAD为等腰直角三角形得PN⊥AD.
由DC⊥AD,N是AD的中点得BN⊥AD.
所以AD⊥平面PBN,
由BC∥AD得BC⊥平面PBN,
那么平面PBC⊥平面PBN.
过点Q作PB的垂线,垂足为H,连接MH.
MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.设CD=1.
在△PCD中,由PC=2,CD=1,PD=2得CE=2,
在△PBN中,由PN=BN=1,PB=3得QH=14,
在Rt△MQH中,QH=14,MQ=2,
所以sin∠QMH=28.
所以,直线CE与平面PBC所成角的正弦值是28.
方法总结 1.证明直线与平面平行的方法.(例:求证:l∥α)
①线面平行的判定定理:在平面α内找到一条与直线l平行的直线m,从而得到l∥α.
②面面平行的性质:过直线l找到(或作出)一个平面β,使得β∥α,从而得l∥α.
③向量法:(i)求出平面α的法向量n和直线l的方向向量l,证明n·l=0,得l∥α.
(ii)证明直线l的方向向量l能被平面α内的两个基底向量所表示,得l∥α.
2.求线面角的方法.
①定义法:作出线面角,解三角形即可.
②解斜线段、射影、垂线段构成的三角形.
例:求AB与平面α所成角θ的正弦值,其中A∈α.只需求出点B到平面α的距离d(通常由等体积法求d),由sin θ=dAB得结论.
③向量法:求出平面α的法向量n,设直线AB与α所成角为θ,则sin θ=|cos|.
最好是画出图形,否则容易出错.
3.(2017课标全国Ⅱ理,19,12分)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=12AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
解析 本题考查了线面平行的证明和线面角、二面角的计算.
(1)取PA的中点F,连接EF,BF.因为E是PD的中点,所以EF∥AD,EF=12AD.由∠BAD=∠ABC=90°得BC∥AD,又BC=12AD,所以EF