几类不同增长的函数模型

几类不同增长的函数模型

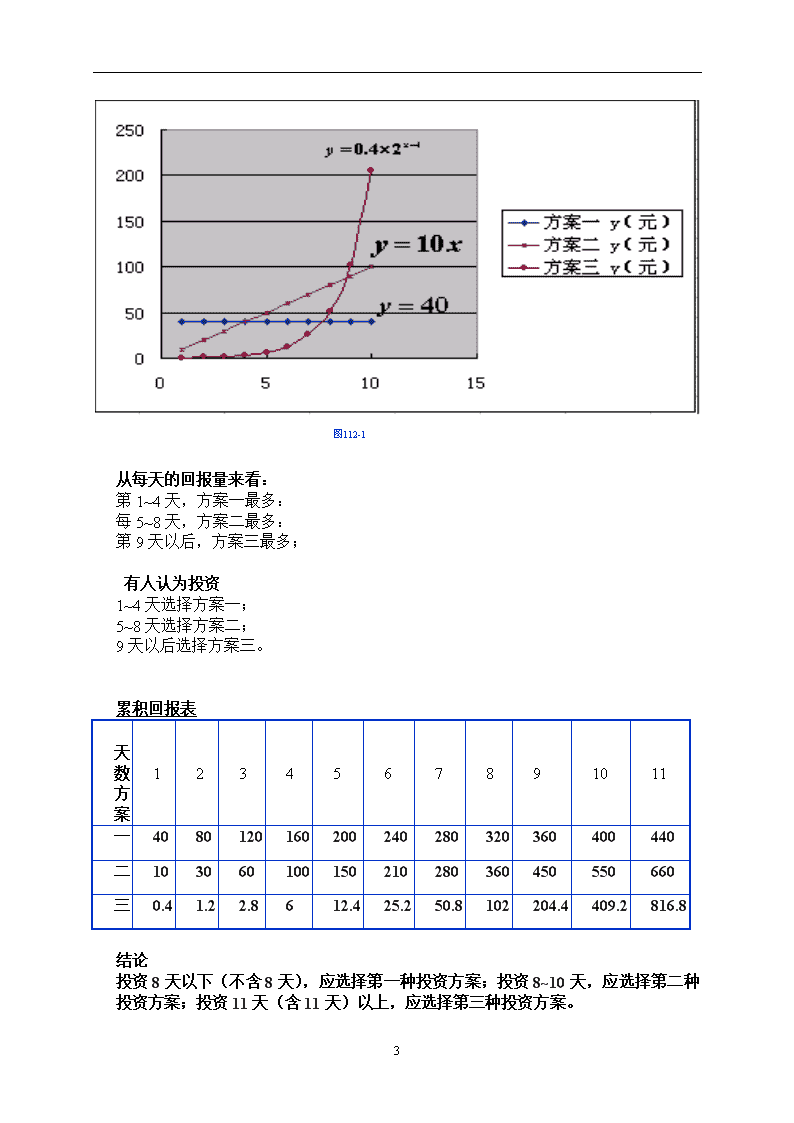
‎ ‎ ‎3.2 函数模型及其应用 ‎ 3.2.1 几类不同增长的函数模型 一、教学目标 （1） 使学生通过投资回报实例，对直线上升和指数爆炸有感性认识。‎ （2） 通过阅读理解题目中文字叙述所反映的实际背景，领悟其中的数学本质，弄清题中出现的量及起数学含义。‎ （3） 体验由具体到抽象及数形结合的思维方法。‎ 二、教学重点与难点 重点：将实际问题转化为函数模型，比教常数函数、一次函数、指数函数模型的增长差异；结合实例让学生体会直线上升，指数爆炸等不同函数型增长的函义。‎ ‎ 难点：怎样选择数学模型分析解决实际问题。‎ 三、教学手段：‎ 运用计算机、实物投影仪等多媒体技术。‎ 四、教材分析：‎ 1、 背景 ‎ ‎ ‎（1） 圆的周长随着圆的半径的增大而增大：‎ L=2πR (一次函数)‎ ‎（2）圆的面积随着圆的半径的增大而增大：‎ S=πR2 (二次函数)‎ ‎（3）某种细胞分裂时，由1个分裂成两 个，两个分裂成4个……，一个这样的细 胞分裂x次后，得到的细胞个数y与x的函数关系是 y = 2x (指数 型函数) 。‎ ‎2、例题 例1、假设你有一笔资金用于投资，现有三种投资方案供你选择，这三种方案的回报如下：‎ 方案一：每天回报40元；‎ 方案二：第一天回报10元，以后每天比前一天多 回报10元；‎ 方案三：第一天回报0.4元，以后每天的回报比前一天翻一番。‎ 请问，你会选择哪种投资方案呢？‎ 投资方案选择原则：‎ 4‎ ‎ ‎ 投入资金相同，回报量多者为优 (1) 比较三种方案每天回报量 ‎(2) 比较三种方案一段时间内的总回报量 哪个方案在某段时间内的总回报量最多，我们就在那段时间选择该方案。‎ x/天 方案一 方案二 方案三 y/元 增长量/元 y/元 增长量/元 y/元 增长量/元 ‎1‎ ‎40‎ ‎0‎ ‎10‎ ‎ ‎ ‎0.4‎ ‎ ‎ ‎2‎ ‎40‎ ‎0‎ ‎20‎ ‎10‎ ‎0.8‎ ‎0.4‎ ‎3‎ ‎40‎ ‎0‎ ‎30‎ ‎10‎ ‎1.6‎ ‎0.8‎ ‎4‎ ‎40‎ ‎0‎ ‎40‎ ‎10‎ ‎3.2‎ ‎1.6‎ ‎5‎ ‎40‎ ‎0‎ ‎50‎ ‎10‎ ‎6.4‎ ‎3.2‎ ‎6‎ ‎40‎ ‎0‎ ‎60‎ ‎10‎ ‎12.8‎ ‎6.4‎ ‎7‎ ‎40‎ ‎0‎ ‎70‎ ‎10‎ ‎25.6‎ ‎12.8‎ ‎8‎ ‎40‎ ‎0‎ ‎80‎ ‎10‎ ‎51.2‎ ‎25.6‎ ‎9‎ ‎40‎ ‎0‎ ‎90‎ ‎10‎ ‎102.4‎ ‎51.2‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎30‎ ‎40‎ ‎0‎ ‎300‎ ‎10‎ ‎214748364.8‎ ‎107374182.4‎ 根据上表我们可以先建立三种投资方案所对应的函数模型，再通过比较它们的增长情况，为选择投资方案提供依据。‎ 解：设第x天所得回报为y元，则 ‎ 方案一：每天回报40元； ‎ ‎ y=40 (x∈N*)‎ 方案二：第一天回报10元，以后每天比前一天多回 报10元； y=10x (x∈N*)‎ 方案三：第一天回报0.4元,以后每天的回报比前一天翻一番。‎ ‎ Y=0.4×2x-1(x)‎ 4‎ ‎ ‎ 图112-1‎ 从每天的回报量来看：‎ 第1~4天，方案一最多： ‎ 每5~8天，方案二最多： ‎ 第9天以后，方案三最多； ‎ ‎ 有人认为投资 ‎1~4天选择方案一；‎ ‎5~8天选择方案二；‎ ‎9天以后选择方案三。‎ 累积回报表 ‎ 天数 方案 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ 一 ‎40‎ ‎80‎ ‎120‎ ‎160‎ ‎200‎ ‎240‎ ‎280‎ ‎320‎ ‎360‎ ‎400‎ ‎440‎ 二 ‎10‎ ‎30‎ ‎60‎ ‎100‎ ‎150‎ ‎210‎ ‎280‎ ‎360‎ ‎450‎ ‎550‎ ‎660‎ 三 ‎0.4‎ ‎1.2‎ ‎2.8‎ ‎6‎ ‎12.4‎ ‎25.2‎ ‎50.8‎ ‎102‎ ‎204.4‎ ‎409.2‎ ‎816.8‎ 结论 投资8天以下（不含8天），应选择第一种投资方案；投资8~10天，应选择第二种投资方案；投资11天（含11天）以上，应选择第三种投资方案。‎ 4‎ ‎ ‎ ‎3．例题的启示：‎ 解决实际问题的步骤：‎ ‎（1）实际问题 ‎ ‎（2）读懂问题抽象概括 ‎（3）数学问题 ‎（4）演算推理 ‎（5）数学问题的解 ‎（6）还原说明 ‎（7）实际问题的解 ‎4．练习 某公司为了实现1000万元利润的目标，准备制定一个激励销售部门的奖励方案：在销售利润达到10万元时，按销售利润进行奖励，且资金y(单位：万元)随着销售利润x (单位：万元)的增加而增加，但资金数不超过5万元，同时奖金不超过利润的25%。现有三个奖励模型：y=0.25x，y=log7x+1，y=1.002x，其中哪个模型能符合公司的要求呢？‎ ‎5．小结 ‎（1）解决实际问题的步骤：‎ 实际问题 读懂问题 将问题抽象化 数学模型 解决问题 ‎ ‎ ‎（2）几种常见函数的增长情况：‎ 常数函数 一次函数 指数函数 没有增长 直线上升 指数爆炸 ‎6．作业:‎ 课本116页练习题集1、2题 4‎