- 2021-06-16 发布 |
- 37.5 KB |
- 30页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习高考专题导数及其应用学案(全国通用)
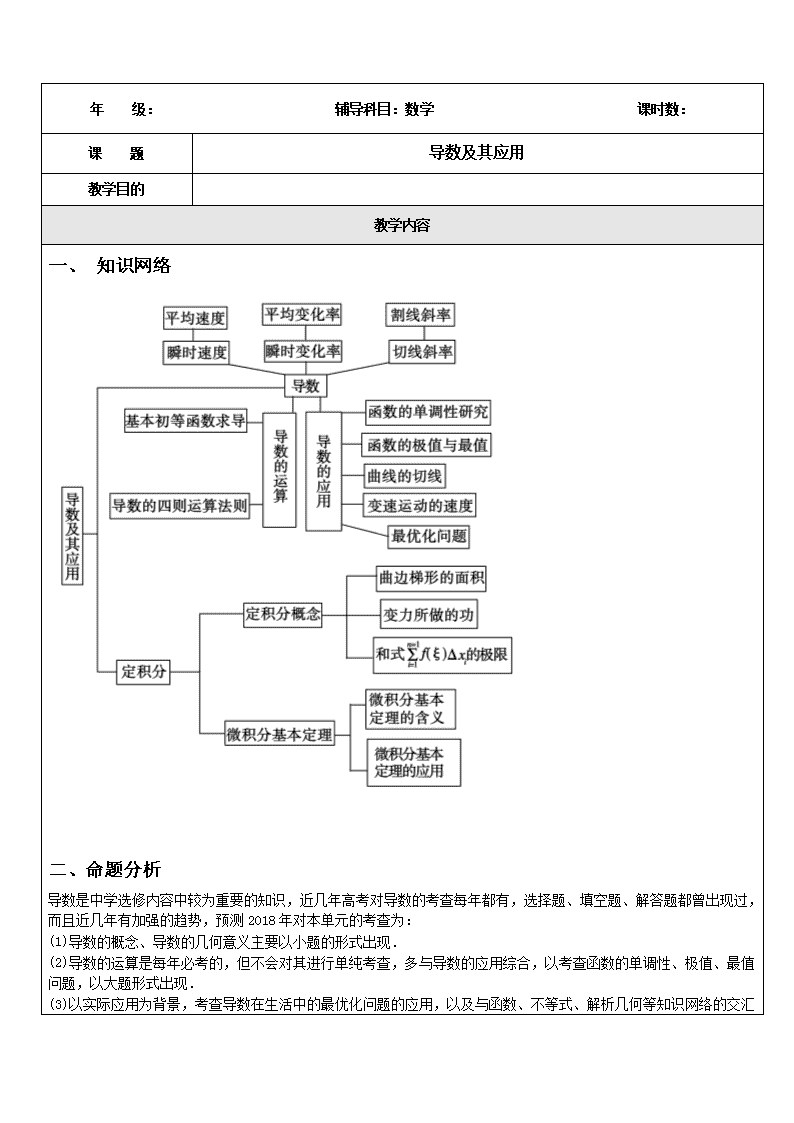
年 级: 辅导科目:数学 课时数: 课 题 导数及其应用 教学目的 教学内容 一、 知识网络 二、命题分析 导数是中学选修内容中较为重要的知识,近几年高考对导数的考查每年都有,选择题、填空题、解答题都曾出现过,而且近几年有加强的趋势,预测2018年对本单元的考查为: (1)导数的概念、导数的几何意义主要以小题的形式出现. (2)导数的运算是每年必考的,但不会对其进行单纯考查,多与导数的应用综合,以考查函数的单调性、极值、最值问题,以大题形式出现. (3) 以实际应用为背景,考查导数在生活中的最优化问题的应用,以及与函数、不等式、解析几何等知识网络的交汇命题,以大题形式出现. (4)(理)定积分也是微积分的核心概念之一,它能解决自然科学和生产实践中的许多问题,如一般平面图形的面积、变速直线运动的路程、变力所做的功等.实际上微积分在物理、化学、生物、天文、地理以及经济等科学领域中都有广泛而重要的应用,因此导数及其应用成为近几年高考的热点. 三、复习建议 1.重视对导数概念的理解,熟练掌握导数的计算公式和导数的几何意义,为导数的应用打下坚实的基础. 2.在复习中,要防止将导数仅仅作为一些规则和步骤来学习,而忽视它的思想和价值. 3.导数的应用较为灵活,是高考中必考的一道解答题,难度为中档题,故复习时要重视求函数的解析式、求函数值域、解决单调性问题、求函数的极值(最值)、构造函数证明不等式等问题.函数是高中数学的重点内容,而函数的性质又是高考命题的热点,而利用导数研究函数的性质比用初等方法研究要方便许多,因此在复习时一定要重视.此外,导数与解析几何或函数的图像的混合问题也是一种重要类型,是高考中考查综合能力的一个方向,应引起重视. 四、知识讲解 第一节 导数及导数的运算 (一)高考目标 考纲解读 1.了解导数概念的实际背景. 2.理解导数的几何意义. 3.(文)能根据导数定义,求函数y=c(c为常数),y=x,y=x2,y=的导数. (理)能根据导数定义,求函数y=c(c)为常数,y=x,y=x2,y=x3,y=,y=的导数. 4.(文)能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数. (理)能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如f(ax+b)的复合函数)的导数. 考向预测 1.导数的几何意义是高考考查的重点内容,常以选择题、填空题的形式出现,有时也出现在解答题中. 2.导数的运算每年必考,一般不单独考查,在考查导数应用的同时考查导数的运算. (二)课前自主预习 知识梳理 1.导数的概念 (1)函数y=f(x)在x=处的导数 ①定义:称函数y=f(x)在x=处的瞬时变化率 = 为函数y=f(x)在x=处的导数,记作f′(x0)或y′|x=,即f′(x0)= = 。 ②几何意义 函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y=f(x)上点 处的 (瞬时速度就是位移函数s(t)对时间t的导数).相应地,切线方程为 . (2)函数f(x)的导函数 称函数f′(x)= 为f(x)的导函数. 2.基本初等函数的导数公式 原函数 导函数 f(x)=c f′(x)=0 f(x)=xn(n∈N*) f′(x)=nxn-1 f(x)=sin x f′(x)=cos x f(x)=cos x f′(x)=-sin x f(x)=ax(a>0且a≠1) f′(x)=axln a f(x)=ex f′(x)=ex f(x)=logax (a>0且a≠1) f′(x)= f(x)=ln x f′(x)= 3.导数的四则运算法则 ①[u(x)±v(x)]′=u′(x)±v′(x). ②[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x). ③[]′=(v(x)≠0). 4.复合函数求导 复合函数y=f(g(x))的导数和y=f(u),u=g(x)的导数之间的关系 为yx′=f′(u)g′(x). (三)基础自测 1.(2018·新课标文)曲线y=x3-2x+1在点(1,0)处的切线方程为( ) A.y=x-1 B.y=-x-1 C.y=2x-2 D.y=-2x-2 [答案] A [解析] 本题考查了导数的几何意义,切线方程的求法,在解题时应首先验证点是否在曲线上,然后通过求导得出切线的斜率,题目定位于简单题. 由题可知,点(1,0)在曲线y=x3-2x+1上,求导可得y′=3x2-2,所以在点(1,0)处的切线的斜率k=1,切线过点(1,0),根据直线的点斜式可得过点(1,0)的曲线y=x3-2x+1的切线方程为y=x-1,故选A. 2.已知函数f(x)在x=1处的导数为3,则f(x)的解析式可能为( ) A.f(x)=(x-1)3+3(x-1) B.f(x)=2(x-1) C.f(x)=2(x-1)2 D.f(x)=x-1 [答案] A [解析] 先求f(x)的导函数,再代入验证.当f(x)=(x-1)3+3(x-1)时,f′(x)=3(x-1)2+3且 f′(1)=3(1-1)2+3=3. 3.与直线2x-y+4=0平行的抛物线y=x2的切线方程是( ) A.2x-y+3=0 B.2x-y-3=0 C.2x-y+1=0 D.2x-y-1=0 [答案] D [解析] 直线2x-y+4=0的斜率为k=2. 由y=x2得y′=2x,令2x=2,得x=1.所以切点为(1,1), 斜率k=2,则所求切线为y-1=2(x-1),即2x-y-1=0为所求. 4.(文)若函数f(x)=x2+bx+c的图像的顶点在第二象限,则函数f ′(x)的图像是( ) [答案] C [解析] 由题意可知在第二象限 ⇒⇒b>0,又f ′(x)=2x+b,故选C. (理)设函数f(x)=x3+x2+tanθ,其中θ∈,则导数f′(1)的取值范围为( ) A.[-2,2] B.[,] C.[,2] D.[,2] [解析] ∵f′(x)=sinθ·x2+cosθ·x, ∴f′(1)=sinθ+cosθ=2sin. ∵θ∈,∴θ+∈. ∴sin∈, ∴f′(1)∈[,2],故选D. 5.(2009·湖北理)已知函数f(x)=f′cosx+sinx,则f的值为________. [答案] 1 [解析] 主要考查导数及函数的求值 f′(x)=-f′sinx+cosx, ∴f′=-f′sin+cos, f′=,∴f′=, ∴f=f′cos+sin=·+=1. 6.(2018·辽宁重点高中联考)函数f(x)=在点(x0,f(x0))处的切线平行于x轴,则f(x0)=________. [答案] [解析] ∵f(x)=,f′(x)=,切线斜率f′(x0)==0,∴x0=e,∴f(x0)=f(e)=. 7.已知曲线S:y=3x-x3及点P(2,2).求过点P的切线方程. [解析] 设切点为(x0,y0), 则y0=3x0-x03.又f′(x)=3-3x2, ∴切线斜率k==3-3x02, 即3x0-x03-2=(x0-2)(3-3x02) ∴(x0-1)[(x0-1)2-3]=0, 解得x0=1或x0=1±, 相应的斜率k=0或k=-9±6. ∴切线方程为y=2或y=(-9±6)(x-2)+2. (四)典型例题 1.命题方向:导数的概念 [例1] (1)若f ′(x0)=2,则 的值为________; (2)若f ′(x0)=A,则 =________. [解析] (1)令-k=Δx,则k=-Δx, ∴原式= =- =-f ′(x0)=-1. (2)原式= = + =A+A=2A. 跟踪练习1: 设函数f(x)在x0点可导,则下列极限等于f ′(x0)的是 ( ) A. B. C. D. [答案] C [解析] 解法1:令x0-Δx=x′0,则当Δx→0时,x′0→x0, 2.命题方向:导数公式及其运算法则 [例2] 求下列函数的导数: (1)y=x5-x3+3x2+; (2)y=(3x3-4x)(2x+1); (3)y=; (4)y=3xex-2x+e; (5)y=; (6)y=xcosx-sinx. (7)y=(1+sinx)2; (8)(理)y=ln; (9)(理)y=cos32x+ex; (10)(理)y=lg. [解析] 可利用导数公式和导数运算法则求导. (1)y′=′-′+(3x2)′+()′=x4-4x2+6x. (2)∵y=(3x3-4x)(2x+1)=6x4+3x3-8x2-4x, ∴y′=24x3+9x2-16x-4, 或y′=(3x3-4x)′(2x+1)+(3x3-4x)(2x+1)′ =(9x2-4)(2x+1)+(3x3-4x)·2=24x3+9x2-16x-4. (3)y′= == (4)y′=(3xex)′-(2x)′+(e)′=(3x)′ex+3x(ex)′-(2x)′ =3xln3·ex+3xex-2xln2=(ln3+1)·(3e)x-2xln2. (5)y′= == (6)y′=(xcosx)′-(sinx)′=cosx-xsinx-cosx=-xsinx. (7)y′=2(1+sinx)·(1+sinx)′=2cosx(1+sinx). (8)(理)y′=′=··(x2+1)′=. (9)(理)y′=3cos22x·(cos2x)′+ex=-6sin2x·cos22x+ex. (10)(理)y′=′=··(1-x2)′=. 跟踪练习2 求下列函数的导数: (1)y=; (2)y=(x+1)(x+2)(x+3); (3)y=-sin; (4)y=+; (5)y=. [解析] (1)∵y==x-+x3+x-2sinx, ∴y′=(x-)′+(x3)′+(x-2sinx)′=-x-+3x2-2x-3sinx+x-2cosx. (2)∵y=(x2+3x+2)(x+3)=x3+6x2+11x+6, ∴y′=3x2+12x+11. (3)∵y=-sin=sinx, ∴y′=′=cosx. (4)y=+==, y′=′==. (5)y′= == 2.命题方向:导数公式及其运算法则 [例2] 求下列函数的导数: (1)y=x5-x3+3x2+; (2)y=(3x3-4x)(2x+1); (3)y=; (4)y=3xex-2x+e; (5)y=; (6)y=xcosx-sinx. (7)y=(1+sinx)2; (8)(理)y=ln; (9)(理)y=cos32x+ex; (10)(理)y=lg. [解析] 可利用导数公式和导数运算法则求导. (1)y′=′-′+(3x2)′+()′=x4-4x2+6x. (2)∵y=(3x3-4x)(2x+1)=6x4+3x3-8x2-4x, ∴y′=24x3+9x2-16x-4,或y′=(3x3-4x)′(2x+1)+(3x3-4x)(2x+1)′ =(9x2-4)(2x+1)+(3x3-4x)·2=24x3+9x2-16x-4. (3)y′===. (4)y′=(3xex)′–(2x)′+(e)′=(3x)′ex+3x(ex)′-(2x)′ =3xln3·ex+3xex-2xln2=(ln3+1)·(3e)x-2xln2. (5)y′===. (6)y′=(xcosx)′-(sinx)′=cosx-xsinx-cosx=-xsinx. (7)y′=2(1+sinx)·(1+sinx)′=2cosx(1+sinx). (8)(理)y′=′=··(x2+1)′=. (9)(理)y′=3cos22x·(cos2x)′+ex=-6sin2x·cos22x+ex. (10)(理)y′=′=··(1-x2)′=. 跟踪练习2 求下列函数的导数: (1)y=; (2)y=(x+1)(x+2)(x+3); (3)y=-sin; (4)y=+; (5)y=. [解析] (1)∵y==x-+x3+x-2sinx, ∴y′=(x-)′+(x3)′+(x-2sinx)′=-x-+3x2-2x-3sinx+x-2cosx. (2)∵y=(x2+3x+2)(x+3)=x3+6x2+11x+6, ∴y′=3x2+12x+11. (3)∵y=-sin=sinx, ∴y′=′=cosx. (4)y=+==, y′=′==. (5)y′===. 3.命题方向:导数的几何意义 [例3] 已知曲线方程为y=x2, (1)求过A(2,4)点且与曲线相切的直线方程; (2)求过B(3,5)点且与曲线相切的直线方程. [解析] (1)∵A(2,4)在y=x2上, 由y=x2得y′=2x,∴y′=4. 因此所求直线的方程为y-4=4(x-2), 即4x-y-4=0. (2)方法1:设过B(3,5)与曲线y=x2相切的直线方程为y-5=k(x-3),即y=kx+5-3k. 由,得:x2-kx+3k-5=0. Δ=-4(3k-5)=0,整理得(k-2)(k-10)=0, ∴k=2或k=10. 所求的直线方程为:2x-y-1=0,或10x-y-25=0. 方法2:设切点P的坐标为(,), 由得y′=2x, y′=2 ,由已知=2,即=2, 将代入上式整理得: =1或=5, ∴切点坐标为(1,1),(5,25), ∴所求直线方程为2x-y-1=0,10x-y-25=0. [点评] (1)解决此类问题一定要分清“在某点处的切线”,还是“过某点的切线”的问法. (2)解决“过某点的切线”问题,一般是设出切点坐标为P(, ),然后求其切线斜率k=f′(),写出其切线方程.而“在某点处的切线”就是指“某点”为切点. (3)曲线与直线相切并不一定只有一个公共点,当曲线是二次曲线时,我们知道直线与曲线相切,有且只有一个公共点,这种观点对一般曲线不一定正确. 跟踪练习3.: 已知函数f(x)=x3+x-16. (1)求曲线y=f(x)在点(2,-6)处的切线的方程; (2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标; (3)如果曲线y=f(x)的某一切线与直线y=-x+3垂直,求切点坐标与切线的方程. [解析] (1)∵f ′(x)=3x2+1, ∴f(x)在点(2,-6)处的切线的斜率为k=f ′(2)=13. ∴切线的方程为y=13x-32. (2)解法1:设切点为(x0,y0), 则直线l的斜率为f ′(x0)=3x02+1, ∴直线l的方程为y=(3x02+1)(x-x0)+x03+x0-16, 又∵直线l过原点(0,0), ∴0=(3x02+1)(-x0)+x03+x0-16, 整理得,x03=-8,∴x0=-2, ∴y0=-26,k=13. ∴直线l的方程为y=13x,切点坐标为(-2,-26). 解法2:设直线l的方程为y=kx,切点为(x0,y0), 则k==, 又∵k=f ′(x0)=3x02+1, ∴=3x02+1,解之得,x0=-2, ∴y0=-26,k=13. ∴直线l的方程为y=13x,切点坐标为(-2,-26). (3)∵切线与直线y=-+3垂直, ∴切线的斜率k=4. 设切点坐标为(x0,y0),则f ′(x0)=3x02+1=4, ∴x0=±1, ∴,或, ∴切线方程为y=4x-18或y=4x-14. (五)思想方法点拨 1.根据导数的定义,求函数y=f(x)在点x0处导数的方法 (1)求函数的增量Δy=f(x0+Δx)-f(x0); (2)求平均变化率=; (3)得导数f′(x0)= . 2.曲线的切线的求法 若已知曲线过点P(x0,y0),求曲线的切线则需分点P(x0,y0)是切点和不是切点两种情况求解. (1)点P(x0,y0)是切点的切线方程y-y0=f′(x0)(x-x0). (2)当点P(x0,y0)不是切点时可分以下几步完成: 第一步:设出切点坐标P′(x1,f(x1)). 第二步:写出过P′(x1,f(x1))的切线方程为y-f(x1)=f′(x1)(x-x1). 第三步:将点P的坐标(x0,y0)代入切线方程求出x1. 第四步:将x1的值代入方程y-f(x1)=f′(x1)(x-x1)可得过点P(x0,y0)的切线方程. 3.函数在点x0处的导数,导函数、导数的区别与联系 (1)函数在一点处的导数f′(x0)是一个常数,不是变量. (2)函数的导数,是针对某一区间内任意点x而言的.函数f(x)在区间(a,b)内每一点都可导,是指对于区间(a,b)内的每一个确定的值x0,都对应着一个确定的导数f′(x0),根据函数的定义,在开区间(a,b)内就构成了一个新的函数,也就是函数f(x)的导函数f′(x). (3)函数y=f(x)在点x0处的导数f′(x0)就是导函数f′(x)在点x=x0处的函数值,即f′(x0) 4.运用复合函数的求导法则y′x=y′u·u′x,应注意以下几个问题: (1)分清楚复合函数的复合关系是由哪些基本函数复合而成,适当选定中间变量; (2)分步计算中的每一步都要明确是对哪个变量求导,而其中特别要注意的是中间变量的系数,如(sin2x)′≠cos2x; (3)根据基本函数的导数公式及导数的运算法则,求出各函数的导数,并把中间变量转换成自变量的函数; (4)复合函数的求导熟练后,中间步骤可以省略不写,不必再写出函数的复合过程,对于经过多次复合及四则运算而成的复合函数,可以直接应用公式和法则.从最外层开始,由外及里逐层求导,即“层层剥皮”. (六)课后强化作业 一、选择题 1.(2018·全国卷Ⅱ文)若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则 ( ) A.a=1,b=1 B.a=-1,b=1 C.a=1,b=-1 D.a=-1,b=-1 [答案] A [解析] 本题考查了导数的概念、运算以及导数的几何意义. y′=2x+a,∴y′|x=0=(2x+a)|x=0=a=1, 将(0,b)代入切线方程得b=1. 2.已知f0(x)=cosx,f1(x)=f ′0(x),f2(x)=f ′1(x),f3(x)=f ′2(x)…,fn+1(x)=f ′n(x),n∈N+,则f2018(x)=( ) A.sinx B.-sinx C.cosx D.-cosx [答案] C [解析] f1(x)=-sinx,f2(x)=-cosx,f3(x)=sinx, f4(x)=cosx,f5(x)=-sinx…,故fn(x)的周期为4, ∴f2018(x)=f0(x)=cosx. 3.若函数f(x)=exsinx,则此函数图像在点(4,f(4))处的切线的倾斜角为( ) A. B.0 C.钝角 D.锐角 [答案] C [解析] f′(x)=exsinx+excosx =ex(sinx+cosx)=exsin(x+). f′(4)=e4sin(4+)<0,则此函数图像在点(4,f(4))处的切线的倾斜角为钝角,故选C. 4.若函数f(x)=sin2x+sinx,则f′(x)是 ( ) A.仅有最小值的奇函数 B.仅有最大值的偶函数 C.既有最大值又有最小值的偶函数 D.非奇非偶函数 [答案] C [解析] f′(x)=2cos2x+cosx-1,显然f′(x)是偶函数,又因为cosx∈[-1,1],所以函数f′(x)既有最大值又有最小值. 5.设a>0,f(x)=ax2+bx+c,曲线y=f(x) 在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,],则P到曲线y=f(x)对称轴距离的取值范围是( ) A. B. C. D. [答案] B [解析] 因f(x)的导数为f ′(x)=2ax+b,又由已知y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为,因此有0≤2ax0+b≤1.而P到曲线y=f(x)的对称轴的距离为=≤. 6.(文)(2018·安徽淮南模拟)若函数f(x)=x3-f′(-1)x2+x+5,则f′(1)的值为( ) A.2 B.-2 C.6 D.-6 [答案] C [解析] ∵f(x)=x3-f′(-1)x2+x+5, ∴f′(x)=x2-2f′(-1)x+1, ∴f′(-1)=(-1)2-2f′(-1)(-1)+1, 解得f′(-1)=-2. ∴f′(x)=x2+4x+1,∴f′(1)=6. (理)设函数f(x)=cos(x+φ)(-π<φ<0),若f(x)+f′(x)是偶函数,则φ的值是( ) A. B. C.- D.- [答案] C [解析] f(x)+f′(x)=cos(x+φ)-sin(x+φ)=2cos,显然当φ=-时,f(x)+f′(x)=2cosx是偶函数. 7.(文)(2018·新课标卷)曲线y=在点(-1,-1)处的切线方程为( ) A.y=2x+1 B.y=2x-1 C.y=-2x-3 D.y=-2x-2 [答案] A [解析] 本小题考查导数的运算,利用导数的几何意义求直线的斜率等. ∵点(-1,-1)在曲线上,且y′==, ∴k=y′|x=-1==2, ∴切线方程为:y+1=2(x+1),即y=2x+1. (理)(2009·安徽理)已知函数f(x)在R上满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是( ) A.y=2x-1 B.y=x C.y=3x-2 D.y=-2x+3 [答案] A [解析] 本题考查函数解析式的求法、导数的几何意义及直线方程的点斜式. ∵f(x)=2f(2-x)-x2+8x-8, ∴f(2-x)=2f(x)-x2-4x+4, ∴f(x)=x2,∴f′(x)=2x, ∴曲线y=f(x)在点(1,f(1))处的切线斜率为2,切线方程为y-1=2(x-1),∴y=2x-1. 8.(文)若点P在曲线y=x3-3x2+(3-)x+上移动,经过点P的切线的斜倾角为α,则角α的取值范围是( ) A. B.∪ C. D.∪ [答案] B [解析] y′=3x2-6x+3-=3(x-1)2-≥- ∴tanα≥- α∈(0,π) ∴α∈∪,故选B. (理)已知函数f(x)=x(x-1)(x-2)…(x-100),则f ′(0)=( ) A.0 B.1002 C.200 D.100! [答案] D [解析] 解法1:f ′(0)= = =[(Δx-1)(Δx-2)…(Δx-100)]=(-1)(-2)…(-100)=100!. 解法2:∵f ′(x)=[x(x-1)(x-2)…(x-100)]′ =x′[(x-1)(x-2)…(x-100)]+x[(x-1)(x-2)…(x-100)]′ =(x-1)(x-2)…(x-100)+x[(x-1)(x-2)…(x-100)]′, ∴f ′(0)=(-1)(-2)…(-100)+0=100!. 解法3:由多项式展开式的性质知,f(x)=a101x101+a100x100+…+a2x2+a1x+a0,则 f ′(x)=b100x100+b99x99+…+b1x+a1,∴f ′(0)=a1. 又a1=(-1)(-2)…(-100)=100!,∴f ′(0)=100!. 二、填空题 9.设直线y=x+b是曲线y=lnx(x>0)的一条切线,则实数b的值为________. [答案] ln2-1 [解析] 由已知条件可得k=(lnx)′==,得切点的横坐标x=2,切点坐标为(2,ln2),由点(2,ln2)在切线y=x+b上可得b=ln2-1. 10.过原点作曲线y=ex的切线,则切点的坐标为________,切线的斜率为________. [答案] (1,e) e 11.点P是曲线y=x2-lnx上任意一点,则P到直线y=x-2的距离的最小值是________. [答案] [解析] 作直线y=x-2的平行线使其与曲线y=x2-lnx相切,则切点到直线y=x-2的距离最小. 由y′=2x-=1,得x=1,或x=-(舍去). ∴切点为(1,1),它到直线x-y-2=0的距离为d===. 三、解答题 12.已知曲线y=x3+. (1)求曲线在点P(2,4)处的切线方程; (2)求曲线过点P(2,4)的切线方程. [分析] (1)在点P处的切线以点P为切点. (2)过点P的切线,点P不一定是切点,需要设出切点坐标. [解析] (1)∵y′=x2, ∴在点P(2,4)处的切线的斜率k=y′=4. ∴曲线在点P(2,4)处的切线方程为y-4=4(x-2), 即4x-y-4=0. (2)设曲线y=x3+与过点P(2,4)的切线相切于点A, 则切线的斜率 ∴切线方程为y-=x02(x-x0), 即y=x02·x-x03+. ∵点P(2,4)在切线上,∴4=2x02-x03+, 即x03-3x02+4=0.∴x03+x02-4x02+4=0. ∴x02(x0+1)-4(x0+1)(x0-1)=0. ∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2. 故所求的切线方程为4x-y-4=0或x-y+2=0. 13.(2018·广州模拟)若存在过点(1,0)的直线与曲线y=x3和y=ax2+x-9都相切,求a的值. [解析] 设过(1,0)的直线与y=x3相切于点(x0,x03), 所以切线方程为y-x03=3x02(x-x0), 即y=3x02x-2x03,又(1,0)在切线上,则x0=0或x0=, 当x0=0时, 由y=0与y=ax2+x-9相切可得a=-, 当x0=时,由y=x-与y=ax2+x-9相切可得a=-1,所以a=-1或-. 14.已知函数f(x)=x3+ax,g(x)=2x2+b,它们的图像在x=1处有相同的切线. (1)求函数f(x)和g(x)的解析式; (2)如果F(x)=f(x)-mg(x)在区间[,3]上是单调增函数,求实数m的取值范围. [解析] (1)f′(x)=3x2+a,g′(x)=4x, 由条件知,∴,∴ ∴f(x)=x3+x,g(x)=2x2. (2)F(x)=f(x)-mg(x)=x3+x-2mx2, ∴F′(x)=3x2-4mx+1, 若F(x)在区间[,3]上为增函数,则需F′(x)≥0, 即3x2-4mx+1≥0,∴m≤. 令h(x)=,x∈[,3],则h(x)在区间[,3]上的最小值是h()=, 因此,实数m的取值范围是m≤. 15.设曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴、y轴所围成的三角形面积为S(t). (1)求切线l的方程; (2)求S(t)的最大值. [解析] (1)因为f ′(x)=(e-x)′=-e-x, 所以切线l的斜率为-e-t, 故切线l的方程为y-e-t=-e-t(x-t), 即e-tx+y-e-t(t+1)=0. (2)令y=0得x=t+1, 又令x=0得y=e-t(t+1), ∵t≥0,∴t+1>0,e-t(t+1)>0, ∴S(t)=(t+1)·e-t(t+1)=(t+1)2e-t, 从而S′(t)=e-t(1-t)(1+t). ∵当t∈(0,1)时,S′(t)>0,当t∈(1,+∞)时,S′(t)<0,所以S(t)的最大值为S(1)=. 第二节 导数的应用 (一)高考目标 考纲解读 1.了解函数单调性和导数的关系,能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次). 2.了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次);会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次). 3.会利用导数解决某些实际问题. 考向预测 1.利用导数研究函数的单调性、极值、最值以及解决生活中的最优化问题,已成为近几年高考炙手可热的考点. 2.选择题、填空题,侧重于利用导数确定函数的单调性和极值;解答题,侧重于导数与函数、解析几何、不等式、数列的综合应用,一般难度较大,属中高档题. (二)课前自主预习 知识梳理 1.函数的单调性 在(a,b)内可导函数f(x),f′(x)在(a,b)任意子区间内都不恒等于0. f′(x)≥0⇔f(x)为 ;f′(x)≤0⇔f(x)为 . 2.函数的极值 (1)判断f(x0)是极值的方法:一般地,当函数f(x)在点x0处连续时, ①如果在x0附近的左侧 ,右侧 ,那么f(x0)是极大值; ②如果在x0附近的左侧 ,右侧 ,那么f(x0)是极小值. (2)求可导函数极值的步骤 ①求f′(x); ②求方程 的根; ③检查f′(x)在方程 的根左右两侧值的符号.如果左正右负,那么f(x)在这个根处取得 ;如果左负右正,那么f(x)在这个根处取得 . 3.函数的最值 (1)在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值. (2)若函数f(x)在[a,b]上单调递增,则 为函数的最小值, 为函数的最大值;若函数f(x)在[a,b]上单调递减,则 为函数的最大值, 为函数的最小值. (3)设函数f(x)在[a,b]上连续,在(a,b)内可导,求f(x)在[a,b]上的最大值和最小值的步骤如下: ①求f(x)在(a,b)内的 ; ②将f(x)的各极值与 比较,其中最大的一个是最大值,最小的一个是最小值. (三)基础自测 1.下面四图都是在同一坐标系中某三次函数及其导函数的图像,其中一定不正确的序号是( ) A.①② B.③④ C.①③ D.①④ [答案] B [解析] 对于③,f(x)在原点附近为增函数,∴f′(x)>0,而图像中当x>0时,f′(x)<0,∴③一定不正确;对于④,同理,导函数开始应在x轴上方,④一定不正确,故选B. 2.已知函数f(x)=x3-px2-qx的图像与x轴切于(1,0)点,则f(x)的极大值、极小值分别为( ) A.,0 B.0, C.-,0 D.0,- [答案] A [解析] f′(x)=3x2-2px-q 由f′(1)=0,f(1)=0得 解得,∴f(x)=x3-2x2+x 由f′(x)=3x2-4x+1=0得x=或x=1 易得当x=时f(x)取极大值 当x=1时f(x)取极小值0. 3.设a∈R,若函数y=ex+ax,x∈R有大于零的极值点,则( ) A.a<-1 B.a>-1 C.a≥- D.a<- [答案] A [解析] y′=ex+a,由条件知,有解, ∴a=-ex<-1. 4.函数y=ax3-x在R上是减函数,则( ) A.a= B.a=1 C.a=2 D.a≤0 [答案] D [解析] y′=3ax2-1, ∵函数y=ax3-x在R上是减函数, ∴3ax2-1≤0在R上恒成立,∴a≤0. 5.函数f(x)=x3-15x2-33x+6的单调减区间为________. [答案] (-1,11) [解析] 本题主要考查求导公式和单调区间. f′(x)=3x2-30x-33=3(x-11)(x+1), 由(x-11)(x+1)<0得-1查看更多