2018届二轮复习函数与方程及函数的应用课件文（全国通用）

2018届二轮复习函数与方程及函数的应用课件文（全国通用）

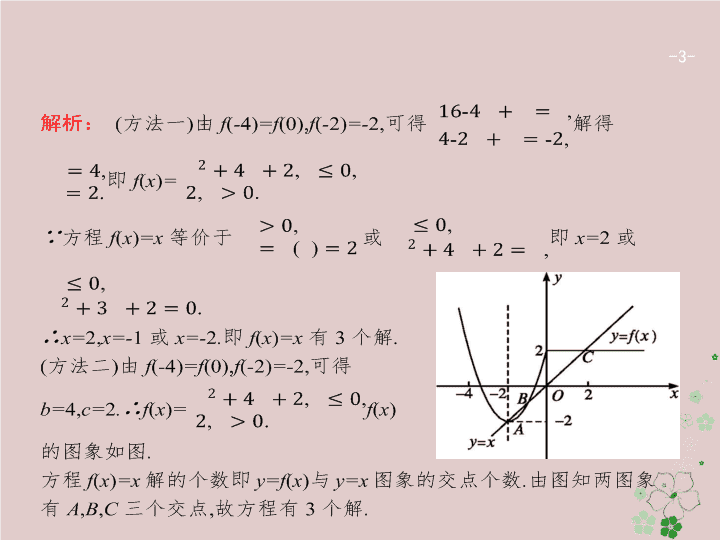
2.2 　函数与方程及函数的应用 - 2 - 热点 1 热点 2 热点 3 - 3 - - 4 - 热点 1 热点 2 热点 3 题后反思 确定函数零点的常用方法 : (1) 解方程判定法 , 方程易求解时用此法 ; (2) 零点存在的判定定理法 , 常常要结合函数的性质、导数等知识 ; (3) 数形结合法 , 如求解含有绝对值、分式、指数、对数、三角式等较复杂的函数零点问题 , 常转化为两个函数图象的交点问题求解 . - 5 - 热点 1 热点 2 热点 3 - 6 - 热点 1 热点 2 热点 3 - 7 - - 8 - - 9 - - 10 - 热点 1 热点 2 热点 3 题后反思 解决由函数零点 ( 方程根 ) 的存在情况求参数的值或取值范围问题 , 关键是利用函数方程思想或数形结合思想 , 构建关于参数的方程或不等式求解 . 对于存在零点求参数范围问题 , 可通过分离参数 , 从而转化为求函数最值问题 . - 11 - 热点 1 热点 2 热点 3 - 12 - - 13 - 热点 1 热点 2 热点 3 - 14 - - 15 - 热点 1 热点 2 热点 3 - 16 - 热点 1 热点 2 热点 3 - 17 - - 18 - 1 . 在求方程解的个数或者根据解的个数求方程中的字母参数的范围问题时 , 数形结合是基本的解题方法 , 即把方程分拆为一个等式 , 使两端都转化为我们所熟悉的函数的解析式 , 然后构造两个函数 f ( x ), g ( x ), 即把方程写成 f ( x ) = g ( x ) 的形式 , 这时方程根的个数就是两个函数图象交点的个数 , 可以根据图象的变化趋势找到方程中字母参数所满足的各种关系 . 2 . 二次函数 y=a ( x-h ) 2 +k ( a ≠0), x ∈ [ p , q ] 的最值问题实际上是函数在 [ p , q ] 上的单调性问题 . 常用方法 :(1) 注意是 “ 轴动区间定 ”, 还是 “ 轴定区间动 ”, 找出分类的标准 ;(2) 利用导数知识 , 最值可以在端点和极值点处寻找 . 3 .f ( x ) ≥ 0 在 [ p , q ] 上恒成立问题 , 等价于 f ( x ) min ≥ 0, x ∈ [ p , q ] . - 19 - - 20 - - 21 - - 22 - - 23 -