- 2021-06-16 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教版(理)第3章第1讲三角函数、解三角形学案
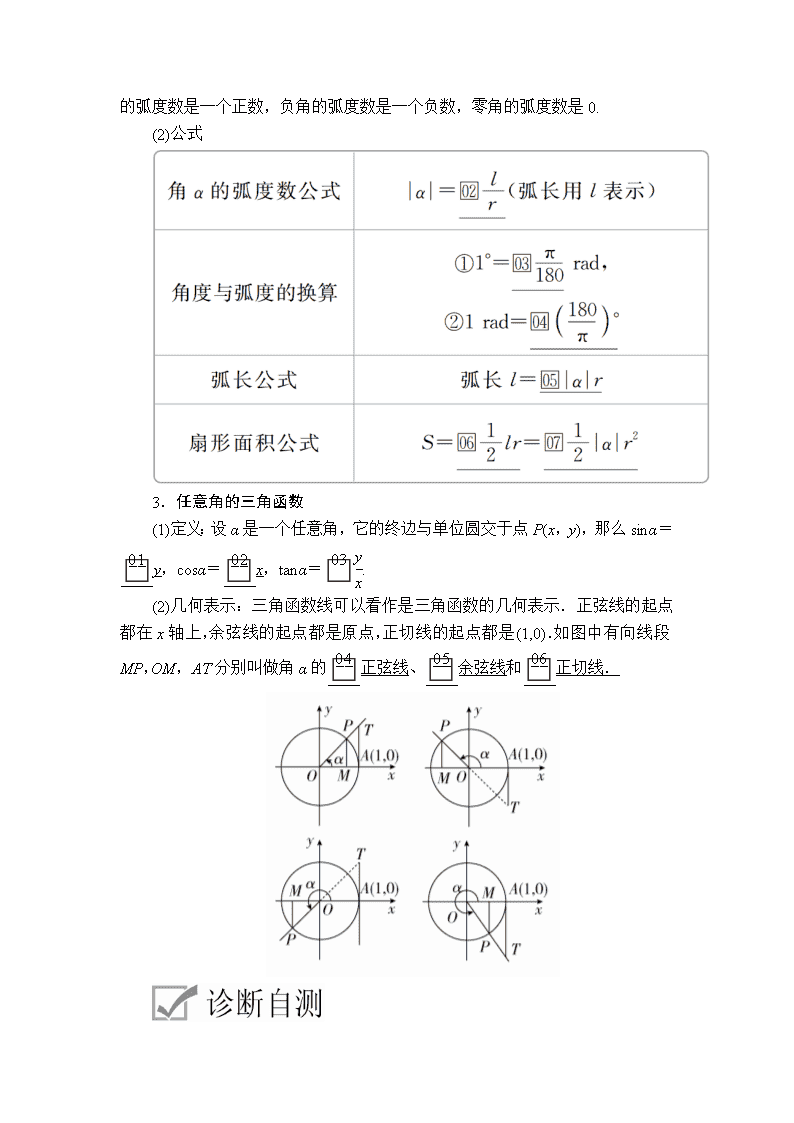
第三章 三角函数、解三角形 第1讲 任意角和弧度制及任意角的三角函数 1.任意角的概念 (1)定义:角可以看成平面内的一条射线绕着端点从一个位置旋转到另一个位置所成的图形. (2)角的分类 (3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z}. 2.弧度制的定义和公式 (1)定义:把长度等于半径 长的弧所对的圆心角叫做1弧度的角.正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0. (2)公式 3.任意角的三角函数 (1)定义:设α是一个任意角,它的终边与单位圆交于点P(x,y),那么sinα=y,cosα=x,tanα=. (2)几何表示:三角函数线可以看作是三角函数的几何表示.正弦线的起点都在x轴上,余弦线的起点都是原点,正切线的起点都是(1,0).如图中有向线段MP,OM,AT分别叫做角α的正弦线、余弦线和正切线. 1.概念辨析 (1)锐角是第一象限的角,第一象限的角也都是锐角.( ) (2)角α的三角函数值与其终边上点P的位置无关.( ) (3)不相等的角终边一定不相同.( ) (4)借助三角函数线可知,若α为第一象限角,则sinα+cosα>1.( ) 答案 (1)× (2)√ (3)× (4)√ 2.小题热身 (1)下列与的终边相同的角的表达式中正确的是( ) A.2kπ+45°(k∈Z) B.k·360°+(k∈Z) C.k·360°-315°(k∈Z) D.kπ+(k∈Z) 答案 C 解析 角度制与弧度制不能混用,排除A,B;因为=2π+,所以与终边相同的角可表示为k·360°+45°(k∈Z)或k·360°-315°等,故选C. (2)若角θ同时满足sinθ<0且tanθ<0,则角θ的终边一定落在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 答案 D 解析 因为sinθ<0,所以θ的终边位于x轴的下方,因为tanθ<0,所以θ的终边在第二、四象限,所以角θ的终边一定落在第四象限. (3)已知扇形的圆心角为120°,其弧长为2π,则此扇形的面积为________. 答案 3π 解析 设此扇形的半径为r,由题意得r=2π,所以r=3,所以此扇形的面积为×2π×3=3π. (4)设角θ的终边经过点P(4,-3),那么2cosθ-sinθ=________. 答案 解析 因为r=|OP|==5,所以cosθ=,sinθ=-,所以2cosθ-sinθ=2×-=. 题型 象限角与终边相同的角 1.(2018·长春一模)若角α的顶点为坐标原点,始边在x轴的非负半轴上,终边在直线y=-x上,则角α的取值集合是( ) A.{α B.{α C.{α D.{α 答案 D 解析 因为直线y=-x的倾斜角是,所以终边落在直线y=-x上的角的取值集合为{α,故选D. 2.与2019°的终边相同,且在0°~360°内的角是________. 答案 219° 解析 因为2019°=5×360°+219°,所以与2019°终边相同的角可表示为k·360°+219°(k∈Z).其中在0°~360°内的角是219°. 3.若角α是第二象限角,则是第________象限角. 答案 一或三 解析 因为角α是第二象限角, 所以2kπ+<α<2kπ+π,k∈Z, 所以kπ+<查看更多