幂函数 (1)

幂函数 (1)

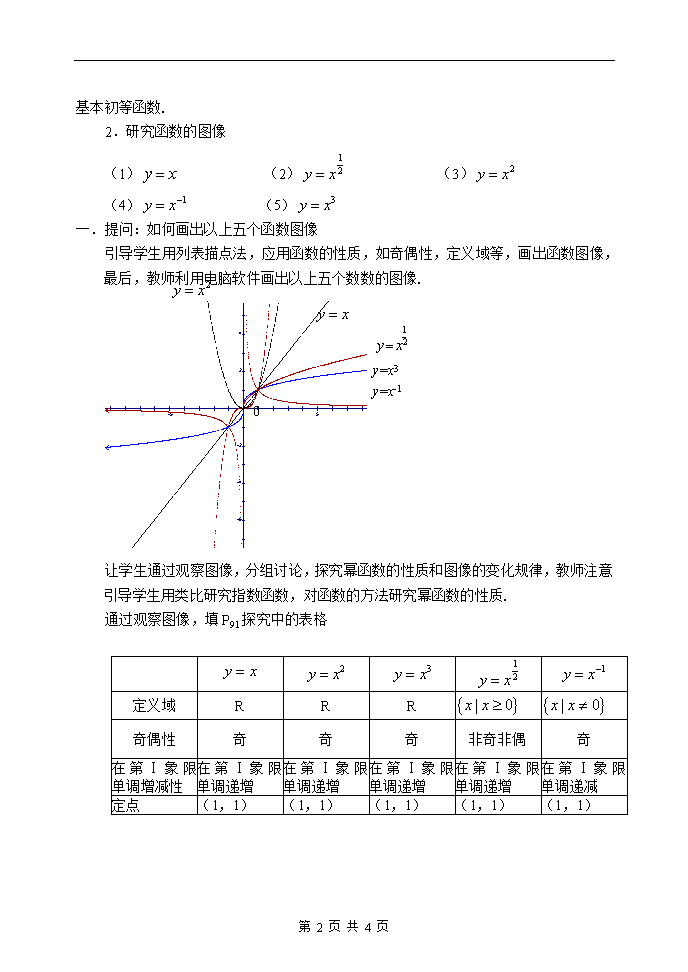
‎ ‎ ‎2.3幂函数 一．教学目标：‎ ‎ 1．知识技能 ‎ （1）理解幂函数的概念；‎ ‎ （2）通过具体实例了解幂函数的图象和性质，并能进行初步的应用.‎ ‎ 2．过程与方法 ‎ 类比研究一般函数，指数函数、对数函数的过程与方法，后研幂函数的图象和性质.‎ ‎3．情感、态度、价值观 ‎ （1）进一步渗透数形结合与类比的思想方法；‎ ‎ （2）体会幂函数的变化规律及蕴含其中的对称性.‎ 二．重点、难点 ‎ 重点：从五个具体的幂函数中认识的概念和性质 ‎ ‎ 难点：从幂函数的图象中概括其性质 ‎ 5．学法与教具 ‎ （1）学法：通过类比、思考、交流、讨论，理解幂函数的定义和性质 ;‎ ‎ （2）教学用具：多媒体 三．教学过程：‎ ‎ 引入新知 ‎ 阅读教材P90的具体实例（1）~（5），思考下列问题.‎ ‎ （1）它们的对应法则分别是什么？‎ ‎ （2）以上问题中的函数有什么共同特征？‎ 让学生独立思考后交流，引导学生概括出结论 答：1、（1）乘以1 （2）求平方 （3）求立方 ‎ ‎（4）求算术平方根 （5）求－1次方 ‎2、上述的问题涉及到的函数，都是形如：，其中是自变量，是常数.‎ 探究新知 ‎ 1．幂函数的定义 一般地，形如（R）的函数称为幂孙函数，其中是自变量，是常数.‎ 如 第 4 页 共 4 页 ‎ ‎ 等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数.‎ ‎2．研究函数的图像 ‎（1） （2） （3） ‎ ‎（4） （5）‎ 一．提问：如何画出以上五个函数图像 引导学生用列表描点法，应用函数的性质，如奇偶性，定义域等，画出函数图像，最后，教师利用电脑软件画出以上五个数数的图像.‎ ‎0‎ y=x-1‎ y=x3‎ 让学生通过观察图像，分组讨论，探究幂函数的性质和图像的变化规律，教师注意引导学生用类比研究指数函数，对函数的方法研究幂函数的性质.‎ 通过观察图像，填P91探究中的表格 定义域 R R R 奇偶性 奇 奇 奇 非奇非偶 奇 在第Ⅰ象限单调增减性 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递减 定点 ‎（1，1）‎ ‎（1，1）‎ ‎（1，1）‎ ‎（1，1）‎ ‎（1，1）‎ 第 4 页 共 4 页 ‎ ‎ ‎3．幂函数性质 ‎ （1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）（原因：）；‎ ‎ （2）＞0时，幂函数的图象都通过原点，并且在[0，+∞]上，是增函数（从左往右看，函数图象逐渐上升）.‎ ‎ 特别地，当＞1，＞1时，∈（0，1），的图象都在图象的下方，形状向下凸越大，下凸的程度越大（你能找出原因吗？）‎ ‎ 当∠α＜1时，∈（0，1），的图象都在的图象上方，形状向上凸，α越小，上凸的程度越大（你能说出原因吗？）‎ ‎ （3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数.‎ ‎ 在第一家限内，当向原点靠近时，图象在轴的右方无限逼近轴正半轴，当慢慢地变大时，图象在轴上方并无限逼近轴的正半轴.‎ ‎ 例题：‎ ‎ 1．证明幂函数上是增函数 ‎ 证：任取＜则 ‎ ‎ ‎ =‎ ‎ =‎ ‎ 因＜0，＞0‎ ‎ 所以，即上是增函数.‎ 思考：‎ 我们知道，若得，你能否用这种作比的方法来证明上是增函数，利用这种方法需要注意些什么？‎ 第 4 页 共 4 页 ‎ ‎ ‎ 2．利用函数的性质 ，判断下列两个值的大小 ‎ （1） （2） （3）‎ 分析：利用幂函数的单调性来比较大小.‎ ‎5．课堂练习 画出的大致图象，并求出其定义域、奇偶性，并判断和证明其单调性.‎ ‎6．归纳小结：提问方式 ‎ ‎（1）我们今天学习了哪一类基本函数，它们定义是怎样描述的？‎ ‎（2）你能根据函数图象说出有关幂函数的性质吗？‎ 作业：P92 习题 2.3 第2、3 题 第 4 页 共 4 页