- 2021-06-16 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
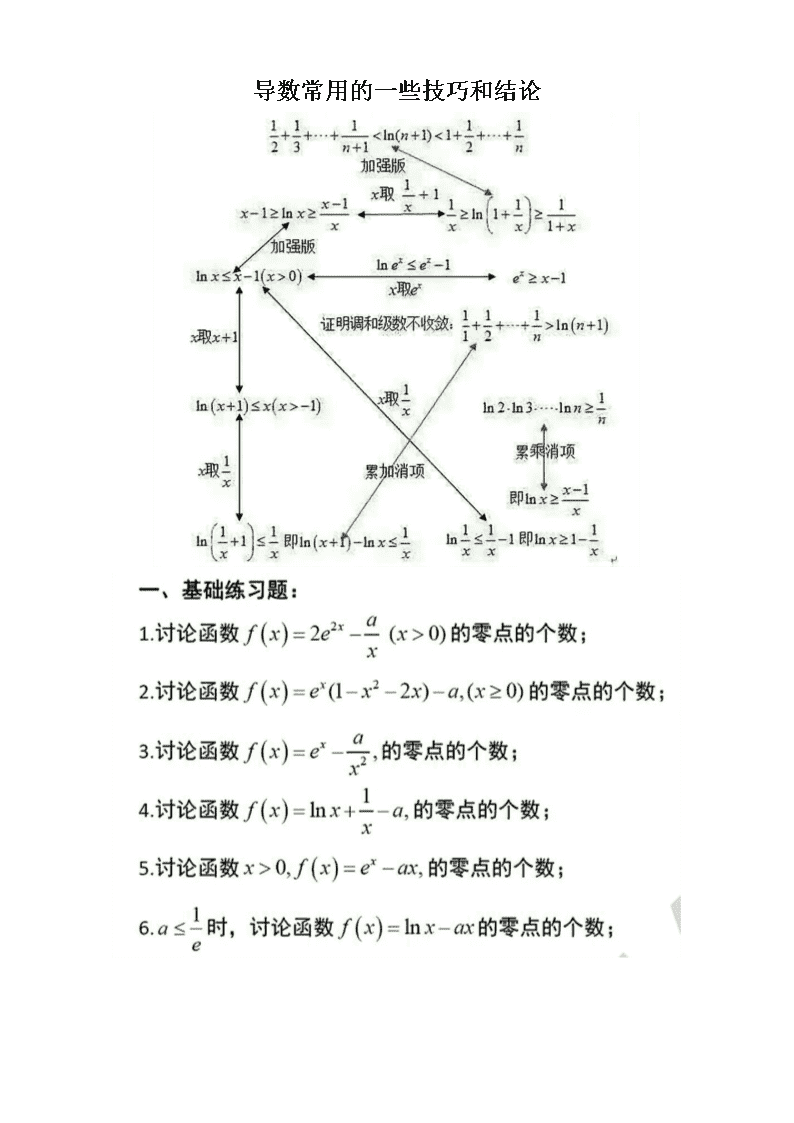
【数学】2021届一轮复习人教A版导数常用的一些技巧和结论学案
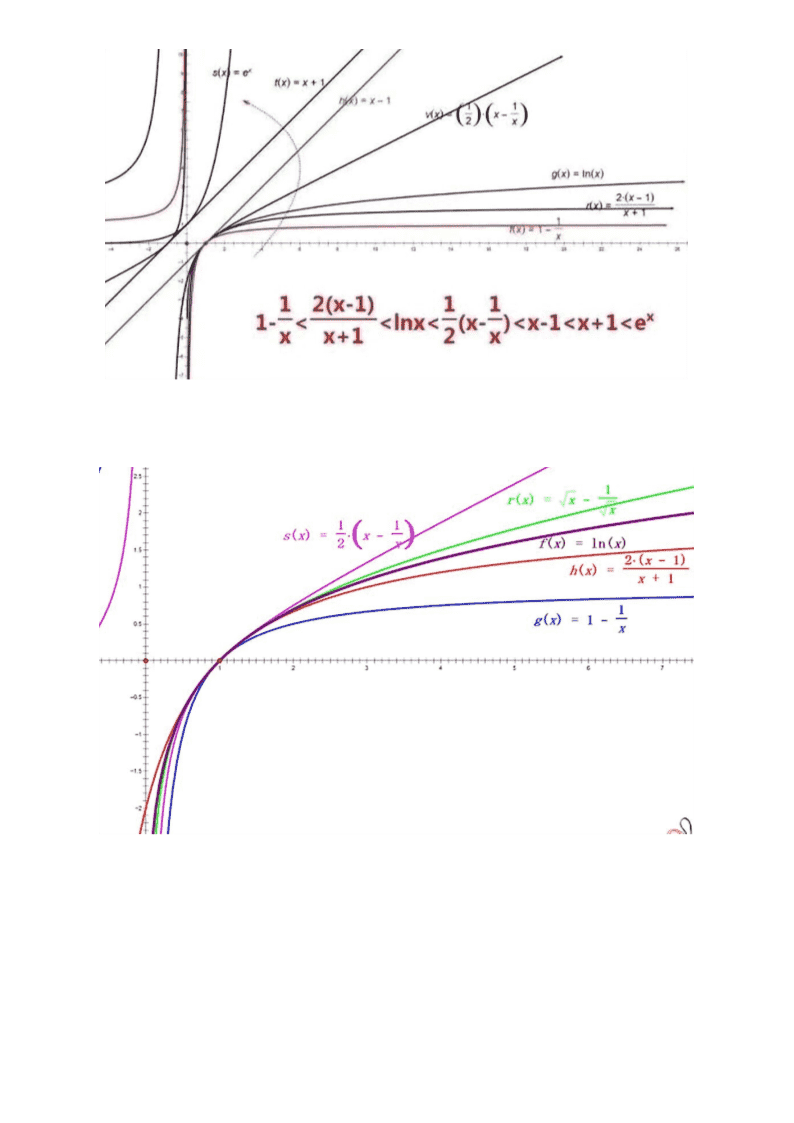
导数常用的一些技巧和结论 (2018年全国新课标1·理·21)已知. (1)讨论的单调性; (2)若有两个零点,求的取值范围. 解析:(1) 若,则恒成立,所以在R上递减; 若,令,得. 当时,,所以在上递减; 当时,,所以在上递增. 综上,当时,在R上递减;当时,在上递减,在上递增. (2)有两个零点,必须满足,即,且. 构造函数,. 易得,所以单调递减. 又因为,所以. 下面只要证明当时,有两个零点即可,为此我们先证明当时,. 事实上,构造函数,易得,∴,所以,即. 当时,, , 其中,,所以在和上各有一个零点. 故的取值范围是. 注意:取点过程用到了常用放缩技巧。 一方面:; 另一方面:时,(目测的) 常用的放缩公式(考试时需给出证明过程) 第一组:对数放缩 (放缩成一次函数),, (放缩成双撇函数),, ,, (放缩成二次函数),, (放缩成类反比例函数),,, ,, 第二组:指数放缩 (放缩成一次函数),,, (放缩成类反比例函数),, (放缩成二次函数),, 第三组:指对放缩 第四组:三角函数放缩 ,,. 第五组:以直线为切线的函数 ,,,,. 几个经典函数模型 经典模型一:或. 【例1】讨论函数的零点个数. (1)时,无零点. ,. (2)时,1个零点. ,. (3)当时,2个零点. (目测),,其中.(放缩) . ,其中.(用到了) (4)当时,1个零点. ,单调递增., . 【变式】(经过换元和等价变形之后均可以转化到例1:): 1. 讨论的零点个数(令,); 2. 讨论的零点个数(令); 3. 讨论的零点个数(考虑); 4. 讨论的零点个数(考虑,令,); 5. 讨论的零点个数(令,); 6. 讨论的零点个数(令). 经典模型二:或 【例2】讨论函数的零点个数. (1)时,1个零点. ,单调递增. 且,,所以在上有一个零点; (2)时,无零点. 恒成立; (3)时,无零点. ; (4)时,2个零点. ,,. 【变式】(经过换元和等价变形之后均可以转化到例题2:): 1. 讨论的零点个数(令,); 2. 讨论的零点个数(去分母后与1等价); 3. 讨论的零点个数(移项平方后与1等价); 4. 讨论的零点个数(移项开方后换元与1等价); 5. 讨论的零点个数(乘以系数e,令); 6. 讨论的零点个数(令,转化成2) 7. 讨论的零点个数(令,); 经典模型三:或 【例】讨论函数的零点个数. (1)时,1个零点. ,单调递增. ,. (2)时,1个零点(). (3)时,无零点. , (4)时,1个零点. . (5)时,2个零点. ,,, 【变式】(经过换元和等价变形之后均可以转化到例题3:): 1.讨论的零点个数; 2. 讨论的零点个数(考虑,令); 3. 讨论的零点个数(令); 4. 讨论的零点个数; 练习题 1. 已知函数有两个零点,求的取值范围. 2. 设函数,讨论的导函数的零点的个数. 3. 已知函数有两个零点,求的取值范围. 4.已知函数. 当时,试讨论的零点的个数.查看更多