【数学】2018届一轮复习人教A版专题七随机变量、空间向量(理科)学案
江苏 新高考
这两部分内容的教学课时都较多,但高考并非是年年都考,通常是交叉式的隔年考一个内容.但2017年两道必做题一改常规,既考查空间向量在立体几何中应用,又考查概率分布与期望值,既考查运算能力,又考查思维能力.,由于考题属中档题要求,所以不宜过难.立体几何题应当容易建立空间直角坐标系,以计算空间角为主;概率题也是离散型随机变量及其分布列的均值与方差、n次独立重复试验的模型及二项分布这几个基本知识交叉考查.
第1课时随机变量与分布列(能力课)
常考题型突破]
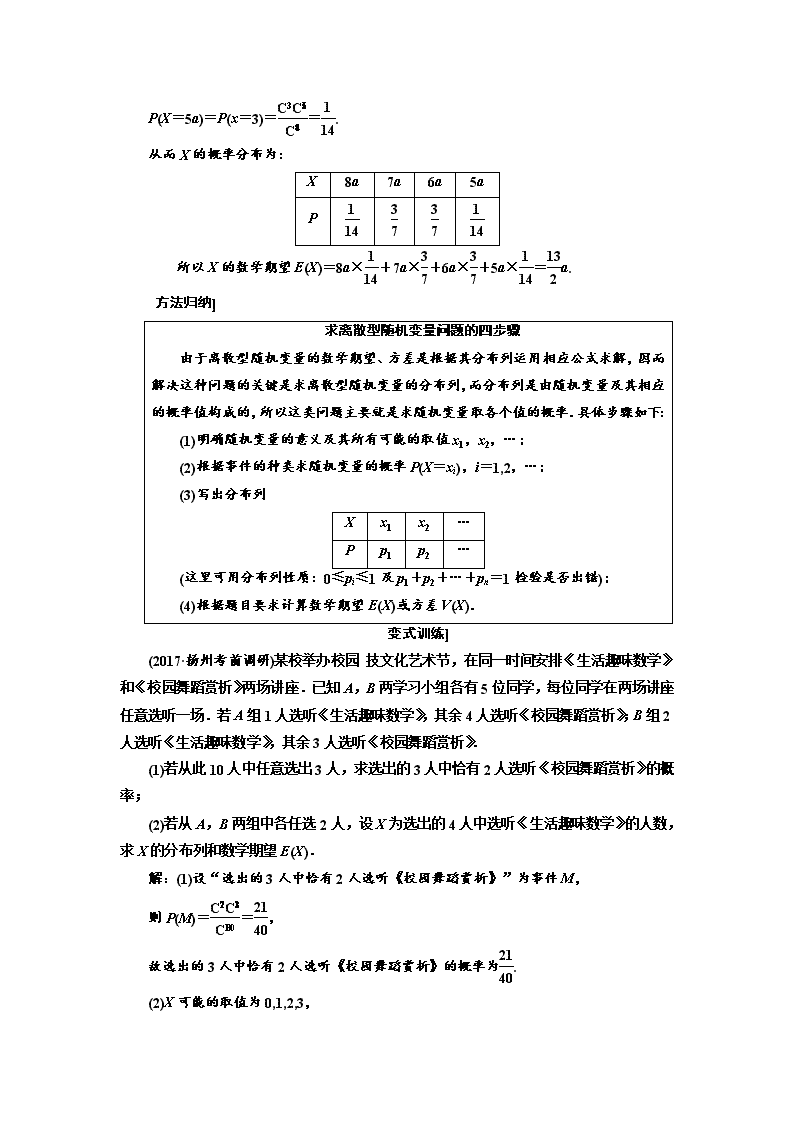
离散型随机变量的分布列及其期望
例1] (2017·南通二调)某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.
(1)求该乐队至少演唱1首原创新曲的概率;
(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a.求观众与乐队的互动指数之和X的概率分布及数学期望.
解] (1)设“至少演唱1首原创新曲”为事件A,
则事件A的对立事件为“没有1首原创新曲被演唱”.
所以P(A)=1-P()=1-=.
答:该乐队至少演唱1首原创新曲的概率为.
(2)设随机变量x表示被演唱的原创新曲的首数,则x的所有可能值为0,1,2,3.
依题意,X=ax+2a(4-x),故X的所有可能值依次为8a,7a,6a,5a.
则P(X=8a)=P(x=0)==,
P(X=7a)=P(x=1)==,
P(X=6a)=P(x=2)==,
P(X=5a)=P(x=3)==.
从而X的概率分布为:
X
8a
7a
6a
5a
P
所以X的数学期望E(X)=8a×+7a×+6a×+5a×=a.
方法归纳]
求离散型随机变量问题的四步骤
由于离散型随机变量的数学期望、方差是根据其分布列运用相应公式求解,因而解决这种问题的关键是求离散型随机变量的分布列,而分布列是由随机变量及其相应的概率值构成的,所以这类问题主要就是求随机变量取各个值的概率.具体步骤如下:
(1)明确随机变量的意义及其所有可能的取值x1,x2,…;
(2)根据事件的种类求随机变量的概率P(X=xi),i=1,2,…;
(3)写出分布列
X
x1
x2
…
P
p1
p2
…
(这里可用分布列性质:0≤pi≤1及p1+p2+…+pn=1检验是否出错);
(4)根据题目要求计算数学期望E(X)或方差V(X).
变式训练]
(2017·扬州考前调研)某校举办校园 技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知A,B两学习小组各有5位同学,每位同学在两场讲座任意选听一场.若A组1人选听《生活趣味数学》,其余4人选听《校园舞蹈赏析》;B组2人选听《生活趣味数学》,其余3人选听《校园舞蹈赏析》.
(1)若从此10人中任意选出3人,求选出的3人中恰有2人选听《校园舞蹈赏析》的概率;
(2)若从A,B两组中各任选2人,设X为选出的4人中选听《生活趣味数学》的人数,求X的分布列和数学期望E(X).
解:(1)设“选出的3人中恰有2人选听《校园舞蹈赏析》”为事件M,
则P(M)==,
故选出的3人中恰有2人选听《校园舞蹈赏析》的概率为.
(2)X可能的取值为0,1,2,3,
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
所以X的概率分布为:
X
0
1
2
3
P
所以X的数学期望E(X)=0×+1×+2×+3×=.
n次独立重复试验的模型及二项分布
例2] (2017·南京、盐城一模)某年级星期一至星期五每天下午排3节课,每天下午随机选择1节作为综合实践课(上午不排该课程),张老师与王老师分别任教甲、乙两个班的综合实践课程.
(1)求这两个班“在星期一不同时上综合实践课”的概率;
(2)设这两个班“在一周中同时上综合实践课的节数”为X,求X的概率分布与数学期望E(X).
解] (1)这两个班“在星期一不同时上综合实践课”的概率为P=1-=.
(2)由题意得X~B,P(X=k)=Ck·5-k,k=0,1,2,3,4,5.
所以X的概率分布为:
X
0
1
2
3
4
5
P
所以X的数学期望为E(X)=5×=.
方法归纳]
二项分布的分布列及期望问题求解三步骤
第一步,先判断随机变量是否服从二项分布,即若满足:①对立性:即一次试验中只有两种结果“成功”和“不成功”,而且有且仅有一个发生;②重复性:试验在相同条件下独立重复地进行n次,保证每一次试验中成功的概率和不成功的概率都保持不变,则该随机变量服从二项分布,否则不服从二项分布.
第二步,若该随机变量服从二项分布,还需要通过古典概型或相互独立事件的概率计算公式计算出试验中“成功”“不成功”的概率分别是多少.
第三步,根据二项分布的分布列列出相应的分布列,再根据期望公式或二项分布期望公式求期望即可.
变式训练]
(2017·扬州期末)为了提高学生学习数学的兴趣,某校决定在每周的同一时间开设《数学史》、《生活中的数学》、《数学与哲学》、《数学建模》四门校本选修课程,甲、乙、丙三位同学每人均在四门校本课程中随机选一门进行学习,假设三人选择课程时互不影响,且每人选择每一课程都是等可能的.
(1)求甲、乙、丙三人选择的课程互不相同的概率;
(2)设X为甲、乙、丙三人中选修《数学史》的人数,求X的概率分布和数学期望E(X).
解:(1)甲、乙、丙三人从四门课程中各任选一门,共有43=64种不同的选法,记“甲、乙、丙三人选择的课程互不相同”为事件M,事件M共包含A=24个基本事件,则P(M)==,所以甲、乙、丙三人选择的课程互不相同的概率为.
(2)法一:X可能的取值为0,1,2,3,
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==.
所以X的概率分布为:
X
0
1
2
3
P
所以X的数学期望E(X)=0×+1×+2×+3×=.
法二:甲、乙、丙三人从四门课程中任选一门,可以看成三次独立重复试验,X为甲、乙、丙三人中选修《数学史》的人数,则X~B,所以P(X=k)=Ck3-k,k=0,1,2,3,
所以X的分布列为:
X
0
1
2
3
P
所以X的数学期望E(X)=3×=.
期望与方差的应用
例3] (2017·苏州模拟)某商场举办“迎新年摸球”
活动,主办方准备了甲、乙两个箱子,其中甲箱中有四个球,乙箱中有三个球(每个球的大小、形状完全相同),每一个箱子中只有一个红球,其余都是黑球.若摸中甲箱中的红球,则可获奖金m元,若摸中乙箱中的红球,则可获奖金n元.活动规定:①参与者每个箱子只能摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③如果在第一个箱子中摸到红球,则可继续在第二个箱子中摸球,否则活动终止.
(1)如果参与者先在乙箱中摸球,求其恰好获得奖金n元的概率;
(2)若要使得该参与者获奖金额的期望值较大,请你帮他设计摸箱子的顺序,并说明理由.
解] (1)设参与者先在乙箱中摸球,且恰好获得奖金n元为事件M.
则P(M)=×=,即参与者先在乙箱中摸球,且恰好获得奖金n元的概率为.
(2)参与者摸球的顺序有两种,分别讨论如下:
①先在甲箱中摸球,参与者获奖金ξ可取0,m,m+n,
则P(ξ=0)=,P(ξ=m)=×=,P(ξ=m+n)=×=,
E(ξ)=0×+m×+(m+n)×=+.
②先在乙箱中摸球,参与者获奖金η可取0,n,m+n,
则P(η=0)=,P(η=n)=×=,P(η=m+n)=×=,
E(η)=0×+n×+(m+n)×=+.
E(ξ)-E(η)=.
当>时,先在甲箱中摸球,再在乙箱中摸球,参与者获奖金期望值较大;
当=时,两种顺序参与者获奖金期望值相等;
当<时,先在乙箱中摸球,再在甲箱中摸球,参与者获奖金期望值较大.
故当>时,先在甲箱中摸球,再在乙箱中摸球,参与者获奖金期望值较大;当=时,两种顺序参与者获奖金期望值相等;当<时,先在乙箱中摸球,再在甲箱中摸球,参与者获奖金期望值较大.
方法归纳]
利用随机变量的均值与方差可以帮助我们作出 学的决策,其中随机变量ξ
的均值的意义在于描述随机变量的平均程度,而方差则描述了随机变量稳定与波动或集中与分散的状况.品种的优劣、仪器的好坏、预报的准确与否、机器的性能好坏等很多指标都与这两个特征量有关.
(1)若我们希望实际的平均水平较理想时,则先求随机变量ξ1,ξ2的均值,当E(ξ1)=E(ξ2)时,不应误认为它们一样好,需要用V(ξ1),V(ξ2) 比较这两个随机变量的偏离程度.
(2)若我们希望比较稳定时,应先考虑方差,再考虑均值是否相等或者接近.
(3)若没有对平均水平或者稳定性有明确要求是,一般先计算均值,若相等,则由方差 确定哪一个更好.若E(ξ1)与E(ξ2)比较接近,且均值较大者的方差较小,显然该变量较好;若E(ξ1)与E(ξ2)比较接近且方差相差不大时,应根据不同选择给出不同的结论,即选择较理想的平均水平还是选择较稳定.
变式训练]
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n
14
15
16
17
18
19
20
频数
10
20
16
16
15
13
10
以100天记录的各需求量的频率作为各需求量发生的概率.
①若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的概率分布、数学期望及方差;
②若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
解:(1)当日需求量n≥16时,y=16×(10-5)=80;
当日需求量n≤15时,y=5n-5(16-n)=10n-80.
所以y=(n∈N).
(2)①X所有可能取值为60,70,80,则P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7.
∴X的概率分布为:
X
60
70
80
P
0.1
0.2
0.7
∴X的数学期望为E(X)=60×0.1+70×0.2+80×0.7=76,
X的方差为V(X)=162×0.1+62×0.2+42×0.7=44.
②答案一:花店一天应购进16枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的概率分布为:
Y
55
65
75
85
P
0.1
0.2
0.16
0.54
∴Y的数学期望为E(Y)=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
Y的方差为V(Y)=(55-76.4)2×0.1+(65-76.4)2×0.2+(75-76.4)2×0.16+(85-76.4)2×0.54=112.04.
由以上的计算结果可以看出,V(X)
0的解集为R的概率.
解:(1)由题意知,这四粒种子中发芽的种子数可能为0,1,2,3,4,对应的未发芽的种子数为4,3,2,1,0,
所以ξ的所有可能取值为0,2,4,
P(ξ=0)=C×2×2=,
P(ξ=2)=C×3×1+C×1×3=,
P(ξ=4)=C×4×0+C×0×4=.
所以随机变量ξ的概率分布为:
ξ
0
2
4
P
数学期望E(ξ)=0×+2×+4×=.
(2)由(1)知ξ的所有可能取值为0,2,4,
当ξ=0时,代入ξx2-ξx+1>0,得1>0,对x∈R恒成立,即解集为R;
当ξ=2时,代入ξx2-ξx+1>0,得2x2-2x+1>0,
即22+>0,对x∈R恒成立,即解集为R;
当ξ=4时,代入ξx2-ξx+1>0,得4x2-4x+1>0,其解集为xx≠,不满足题意.
所以不等式ξx2-ξx+1>0的解集为R的概率P=P(ξ=0)+P(ξ=2)=.
5.(2017·天津高考)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为,,.
(1)记X表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X的分布列和数学期望;
(2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
解:(1)随机变量X的所有可能取值为0,1,2,3.
P(X=0)=××=,
P(X=1)=××+××+××=,
P(X=2)=××+××+××=,
P(X=3)=××=.
所以随机变量X的分布列为:
X
0
1
2
3
P
随机变量X的数学期望E(X)=0×+1×+2×+3×=.
(2)设Y表示第一辆车遇到红灯的个数,Z表示第二辆车遇到红灯的个数,则所求事件的概率为
P(Y+Z=1)=P(Y=0,Z=1)+P(Y=1,Z=0)
=P(Y=0)P(Z=1)+P(Y=1)P(Z=0)
=×+×=.
所以这2辆车共遇到1个红灯的概率为.
6.(2017·全国卷Ⅲ)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间 20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温
10,15)
15,20)
20,25)
25,30)
30,35)
35,40)
天数
2
16
36
25
7
4
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
解:(1)由题意知,X所有可能取值为200,300,500,
由表格数据知
P(X=200)==0.2,P(X=300)==0.4,
P(X=500)==0.4.
因此X的分布列为:
X
200
300
500
P
0.2
0.4
0.4
(2)由题意知,这种酸奶一天的需求量至多为500,至少为200,因此只需考虑200≤n≤500.
当300≤n≤500时,
若最高气温不低于25,则Y=6n-4n=2n;
若最高气温位于区间 20,25),则Y=6×300+2(n-300)-4n=1 200-2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n.
因此EY=2n×0.4+(1 200-2n)×0.4+(800-2n)×0.2=640-0.4n.
当200≤n<300时,
若最高气温不低于20,则Y=6n-4n=2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n.
因此EY=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n.
所以n=300时,Y的数学期望达到最大值,最大值为520元.
第2课时运用空间向量求角(能力课)
常考题型突破]
运用空间向量求两直线所成的角
例1] 已知正三棱柱ABCA1B1C1的各条棱长都相等,P为A1B上的点,且=λ,PC⊥AB.
(1)求λ的值;
(2)求异面直线PC与AC1所成角θ的余弦值.
解] (1)设正三棱柱的棱长为2,取AC中点O,连结OB,则OB⊥AC.以O为原点,OB,OC所在直线为x轴,y轴,过点O且平行AA1的直线为z轴,建立如图所示的空间直角坐标系,
则A(0,-1,0),B(,0,0),C(0,1,0),A1(0,-1,2),B1(,0,2),C1(0,1,2),
所以=(,1,0),=(0,-2,2),=(,1,-2).
因为PC⊥AB,所以·=0,
得(+)·=0,
即(+λ)·=0,
即(λ,-2+λ,2-2λ)·(,1,0)=0,解得λ=.
(2)由(1)知=,=(0,2,2),cos θ==,
所以异面直线PC与AC1所成角θ的余弦值是.
方法归纳]
1.两条异面直线所成角的求法
设两条异面直线a,b的方向向量分别为a,b,其夹角为θ,则cos φ=|cos θ|=(其中φ为异面直线a,b所成的角).
2.用向量法求异面直线所成角的四步骤
(1)选择三条两两垂直的直线建立空间直角坐标系;
(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量;
(3)利用向量的夹角公式求出向量夹角的余弦值;
(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.
变式训练]
(2017·无锡期末)如图,四棱锥PABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点.
(1)求EF与DG所成角的余弦值;
(2)若M为EF上一点,N为DG上一点,是否存在MN,使得MN⊥平面PBC?若存在,求出点M,N的坐标;若不存在,请说明理由.
解:(1)以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,1),
∵E,F,G分别为BC,PD,PC的中点,
∴E,F,G,
∴=,=,
设EF与DG所成角为θ,
则cos θ==.
∴EF与DG所成角的余弦值为.
(2)存在MN,使得MN⊥平面PBC,理由如下:
设平面PBC的法向量为n=(x,y,z),
∵=(0,1,0),=(1,0,-1),
∴即
取x=1,得n=(1,0,1),
若存在MN,使得MN⊥平面PBC,则∥n,
设M(x1,y1,z1),N(x2,y2,z2),
则 ①
∵点M,N分别是线段EF与DG上的点,
∴=λ,=t,
∵=,=(x2,y2-2,z2),
∴且 ②
把②代入①,得
解得∴M,N.
故存在两点M,N,使得MN⊥平面PBC.
运用空间向量求直线和平面所成的角
例2] (2017·镇江调研)如图,在棱长为3的正方体ABCDA1B1C1D1中,A1E=CF=1.
(1)求两条异面直线AC1与BE所成角的余弦值;
(2)求直线BB1与平面BED1F所成角的正弦值.
解] (1)以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系Dxyz,如图所示,
则A(3,0,0),C1(0,3,3),B(3,3,0),E(3,0,2),=(-3,3,3),=(0,-3,2),
所以cos〈,〉=
==-,
故两条异面直线AC1与BE所成角的余弦值为.
(2)由(1)知=(0,-3,2),又D1(0,0,3),B1(3,3,3),
所以=(3,0,-1),=(0,0,3).
设平面BED1F的法向量为n=(x,y,z),
则即令x=1,得y=2,z=3,n=(1,2,3)是平面BED1F的一个法向量.
设直线BB1与平面BED1F所成的角为α,则
sin α===,
所以直线BB1与平面BED1F所成角的正弦值为.
方法归纳]
直线和平面所成的角的求法
如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sin φ=|cos θ|=.
变式训练]
(2017·南通、泰州一调)如图所示,在棱长为2的正方体ABCDA1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).
(1)若λ=,求AP与AQ所成角的余弦值;
(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.
解:以{,,}为正交基底,建立如图所示空间直角坐标系Axyz.
则A(0,0,0),A1(0,0,2),P(1,2,2),Q(2,0,2λ).
(1)当λ=时,=(1,2,2),=(2,0,1),
所以cos〈,〉=
==.
所以AP与AQ所成角的余弦值为.
(2)=(0,0,2),=(2,0,2λ).
设平面APQ的法向量为n=(x,y,z),
则即
令z=-2,则x=2λ,y=2-λ.
所以n=(2λ,2-λ,-2).
又因为直线AA1与平面APQ所成角为45°,
所以|cos〈n,〉|=
==,
可得5λ2-4λ=0,又因为λ≠0,所以λ=.
运用空间向量求二面角
例3] (2017·南通调研)如图,在四棱锥SABCD中,底面ABCD为矩形,SA⊥平面ABCD,AB=1,AD=AS=2,P是棱SD上一点,且SP=PD.
(1)求直线AB与CP所成角的余弦值;
(2)求二面角APCD的余弦值.
解] (1)如图,分别以AB,AD,AS所在直线为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),S(0,0,2).
设P(x0,y0,z0),
由=,得(x0,y0,z0-2)=(0,2,-2),
∴x0=0,y0=,z0=,
点P的坐标为.
=,=(1,0,0).
设直线AB与CP所成的角为α,
则cos α==.
(2)设平面APC的法向量为m=(x1,y1,z1),
由于=(1,2,0),=,
∴即
令y1=-2,则x1=4,z1=1,
所以m=(4,-2,1)为平面APC的一个法向量.
设平面SCD的法向量为n=(x2,y2,z2),
由于=(1,0,0),=(0,-2,2),
∴即
令y2=1,则z2=1,
所以n=(0,1,1)为平面SCD的一个法向量.
设二面角APCD的大小为θ,由图易知θ为锐角,
所以cos θ=|cos〈m,n〉|==,
所以二面角APCD的余弦值为.
方法归纳]
解决二面角问题的两种方法
(1)坐标法
建立恰当坐标系,求出两个平面的法向量n1,n2,利用cos〈n1,n2〉=求出.(结合图形取“±”号)
(2)定义法
构造出二面角的平面角,通过解三角形计算.
变式训练]
1.直三棱柱ABCA1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,=λ.
(1)若λ=1,求直线DB1与平面A1C1D所成角的正弦值;
(2)若二面角B1A1C1D的大小为60°,求实数λ的值.
解:如图,分别以AB,AC,AA1所在的直线为x轴,y轴,z轴建立空间直角坐标系Axyz.
则A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,2),B1(2,0,2),C1(0,4,2).
(1)当λ=1时,D为BC的中点,所以D(1,2,0),=(1,-2,2),=(0,4,0),=(1,2,-2).
设平面A1C1D的法向量为n=(x,y,z),
则即
令z=1,得y=0,x=2,
则n=(2,0,1)为平面A1C1D的一个法向量,
设直线DB1与平面A1C1D所成角为θ.
则sin θ====,
所以直线DB1与平面A1C1D所成角的正弦值为.
(2)因为=λ,所以D,=.
设平面A1C1D的法向量为n1=(x1,y1,z1),
则即
令z1=1,得y1=0,x1=λ+1,
则n1=(λ+1,0,1)为平面A1C1D的一个法向量.
又平面A1B1C1的一个法向量为n2=(0,0,1),
由题意得|cos〈n1,n2〉|=,所以=,
解得λ=-1或λ=--1(不合题意,舍去),
所以实数λ的值为-1.
2.(2017·苏锡常镇一模)如图,已知正四棱锥PABCD中,PA=AB=2,点M,N分别在PA,BD上,且==.
(1)求异面直线MN与PC所成角的大小;
(2)求二面角NPCB的余弦值.
解:(1)连结AC,BD,设AC,BD交于点O,在正四棱锥PABCD中,OP⊥平面ABCD.又PA=AB=2,所以OP=.以O为坐标原点,,方向分别是x轴,y轴正方向,建立空间直角坐标系Oxyz,如图.
则A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),P(0,0,).
故=+=+=,==,
所以=,=(-1,1,-),
cos〈,〉===,
所以MN与PC所成角的大小为30°.
(2)=(-1,1,-),=(2,0,0),=.
设m=(x,y,z)是平面PCB的一个法向量,
则即
令y=,得z=1,所以m=(0,,1),
设n=(x1,y1,z1)是平面PCN的一个法向量,
则即
令x1=2,得y1=4,z1=,
所以n=(2,4,),
故cos〈m,n〉===,
所以二面角NPCB的余弦值为.
课时达标训练]
1.(2017·南京、盐城二模)如图,在直四棱柱ABCDA1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=60°,E,F分别是BC,A1C的中点.
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上,=λ.若CM∥平面AEF,求实数λ的值.
解:因为四棱柱ABCDA1B1C1D1为直四棱柱,所以A1A⊥平面ABCD.
又AE⊂平面ABCD,AD⊂平面ABCD,
所以A1A⊥AE,A1A⊥AD.
在菱形ABCD中,∠ABC=60°,则△ABC是等边三角形.
因为E是BC的中点,所以BC⊥AE.
因为BC∥AD,所以AE⊥AD.
故以A为原点,AE,AD,AA1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.则A(0,0,0),E(,0,0),C(,1,0),D(0,2,0),A1(0,0,2),F.
(1)因为=(0,2,0),=,
所以cos〈,〉==,
所以异面直线EF,AD所成角的余弦值为.
(2)设M(x,y,z),由于点M在线段A1D上,且 =λ,即=λ,
则(x,y,z-2)=λ(0,2,-2).
解得M(0,2λ,2-2λ),=(-,2λ-1,2-2λ).
设平面AEF的法向量为n=(x0,y0,z0).
因为=(,0,0),=,
所以即
令y0=2,得z0=-1,
所以平面AEF的一个法向量为n=(0,2,-1).
由于CM∥平面AEF,则n·=0,
即2(2λ-1)-(2-2λ)=0,解得λ=.
2.如图,已知四棱锥PABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=AB=1,M是PB的中点.
(1)证明:平面PAD⊥平面PCD;
(2)求AC与PB所成角的余弦值;
(3)求平面AMC与平面BMC所成二面角(锐角)的余弦值.
解:建立如图所示的空间直角坐标系,则A(0,0,0),D(1,0,0),P(0,0,1),B(0,2,0),C(1,1,0),M.
(1)证明:因为=(0,0,1),=(0,1,0),故·=0,所以AP⊥DC.由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,
所以DC⊥平面PAD.
又DC⊂平面PCD,所以平面PAD⊥平面PCD.
(2)因为=(1,1,0),=(0,2,-1),
所以cos〈,〉===.
所以AC与PB所成角的余弦值为.
(3)设平面AMC的一个法向量为n1=(x1,y1,z1).
因为=,=(1,1,0),
所以即
取x1=1,得y1=-1,z1=2,所以n1=(1,-1,2).
同理可得平面BMC的一个法向量为n2=(1,1,2).
因为cos〈n1,n2〉===.
所以平面AMC与平面BMC所成二面角(锐角)的余弦值为.
3.(2017·江苏高考)如图,在平行六面体ABCDA1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=,∠BAD=120°.
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角BA1DA的正弦值.
解:(1)在平面ABCD内,过点A作AE⊥AD,交BC于点E.
因为AA1⊥平面ABCD,
所以AA1⊥AE,AA1⊥AD.
如图,以{,,}为正交基底,建立空间直角坐标系Axyz.
因为AB=AD=2,
AA1=,∠BAD=120°,
则A(0,0,0),B(,-1,0),D(0,2,0),E(,0,0),A1(0,0,),C1(,1,).
(1)=(,-1,-),=(,1,).
则cos〈,〉===-.
因此异面直线A1B与AC1所成角的余弦值为.
(2)可知平面A1DA的一个法向量为=(,0,0).
设m=(x,y,z)为平面BA1D的一个法向量,
又=(,-1,-),=(-,3,0),
则即
不妨取x=3,则y=,z=2,
所以m=(3,,2)为平面BA1D的一个法向量,
从而cos〈,m〉===.
设二面角BA1DA的大小为θ,则|cos θ|=.
因为θ∈ 0,π],所以sin θ==.
因此二面角BA1DA的正弦值为.
4.如图,在直三棱柱ABCA1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足=λ (0≤λ≤1).
(1)若λ=,求直线PC与平面A1BC所成角的正弦值;
(2)若二面角PA1CB的正弦值为,求λ的值.
解:以A为坐标原点,分别以AB,AC,AA1所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系Axyz.因为AB=AC=1,AA1=2,则A(0,0,0),B(1,0,0),C(0,1,0),A1(0,0,2),B1(1,0,2),P(1,0,2λ).
(1)由λ=得,=,=(1,0,-2),=(0,1,-2).
设平面A1BC的法向量为n1=(x1,y1,z1),
由得
不妨取z1=1,则x1=y1=2,
从而平面A1BC的一个法向量为n1=(2,2,1).
设直线PC与平面A1BC所成的角为θ,
则sin θ===,
所以直线PC与平面A1BC所成角的正弦值为.
(2)设平面PA1C的法向量为n2=(x2,y2,z2),
又=(1,0,2λ-2),
故由得
不妨取z2=1,则x2=2-2λ,y2=2,
所以平面PA1C的一个法向量为n2=(2-2λ,2,1).
则cos〈n1,n2〉=,
又二面角PA1CB的正弦值为,
所以=,
化简得λ2+8λ-9=0,解得λ=1或λ=-9(舍去),
故λ的值为1.
5.如图,正四棱柱ABCDA1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.
(1)设二面角AA1BP的大小为θ,求sin θ的值;
(2)设M为线段A1B上的一点,求的取值范围.
解:(1)如图,以点D为坐标原点,DA,DC,DD1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系Dxyz,则A(1,0,0),A1(1,0,2),P(0,1,1),B(1,1,0).
所以=(0,0,2),=(0,1,0).
设平面AA1B的法向量为n=(x1,y1,z1),
则即
取n=(1,0,0)为平面AA1B的一个法向量.
又=(1,-1,1),=(1,0,-1).
设平面PA1B的法向量为m=(x2,y2,z2),
则即
取m=(1,2,1)为平面PA1B的一个法向量.
所以cos〈n,m〉==,
则sin θ=.
(2)设M(x,y,z),=λ (0≤λ≤1),
即(x-1,y-1,z)=λ(0,-1,2),
所以M(1,1-λ,2λ).
所以=(0,λ-1,-2λ),=(-1,λ,1-2λ),
=
=
=.
令2λ-1=t∈ -1,1],
则=,
当t∈ -1,0)时,∈;
当t∈(0,1]时,∈;
当t=0时,=0.
所以∈,
则∈.
故的取值范围为.
6.(2017·南通三模)如图,在四棱锥SABCD中,SD⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=∠DAB=90°,SD=AD=AB=2,DC=1.
(1)求二面角SBCA的余弦值;
(2)设P是棱BC上一点,E是SA的中点,若PE与平面SAD所成角的正弦值为,求线段CP的长.
解:(1)以D为坐标原点,DA,DC,DS所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系Dxyz,
则D(0,0,0),A(2,0,0),B(2,2,0),C(0,1,0),S(0,0,2),
所以=(2,2,-2),=(0,1,-2),=(0,0,2).
设平面SBC的法向量为n1=(x,y,z),
则即
令z=1,得x=-1,y=2,
所以n1=(-1,2,1)是平面SBC的一个法向量.
因为SD⊥平面ABC,取平面ABC的一个法向量n2=(0,0,1).
设二面角SBCA的大小为θ,
由图可知二面角SBCA为锐二面角,
所以|cos θ|===,
所以二面角SBCA的余弦值为.
(2)由(1)知E(1,0,1),
=(2,1,0),=(1,-1,1).
设=λ (0≤λ≤1),
则=λ(2,1,0)=(2λ,λ,0),
所以=-=(1-2λ,-1-λ,1).
易知CD⊥平面SAD,
所以=(0,1,0)是平面SAD的一个法向量.
设PE与平面SAD所成的角为α,
所以sin α=|cos〈,〉|==,
即=,得λ=或λ=(舍去).
所以=,||=,
所以线段CP的长为.