- 2021-06-16 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
湖北省钢城四中2019-2020学年高一上学期期中考试数学试卷
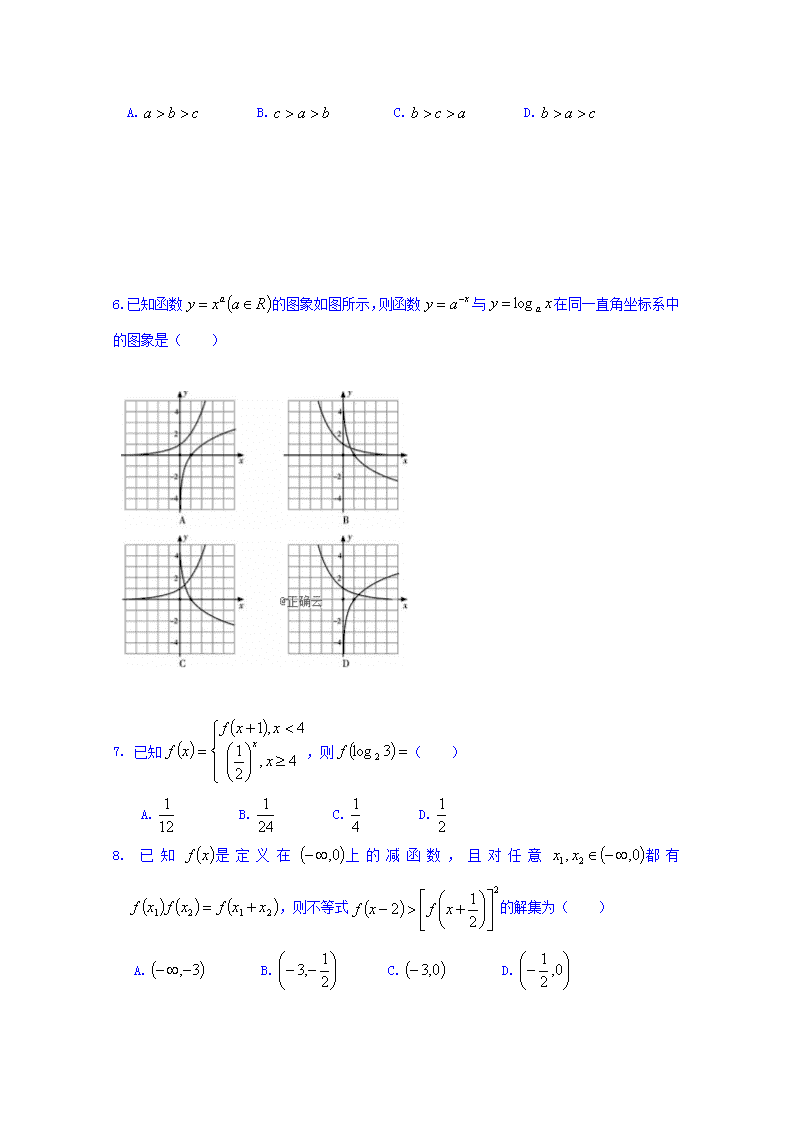
www.ks5u.com 数学试卷 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的). 1. 已知集合,则= ( ) A. B. C. D. 2. 函数的值域是( ) A. B. C. D. 3. 函数的图象必经过点( ) A. B. C. D. 4. 下图是对数函数y=logax的图象,已知a值取,,,,则图象C1,C2,C3,C4对应的a值依次是 ( ) A. ,,, B. ,,, C.,,, D. ,,, 5.设(为自然对数的底数,),则的大小关系为( ) A. B. C. D. 6.已知函数的图象如图所示,则函数与在同一直角坐标系中的图象是( ) 7. 已知,则( ) A. B. C. D. 8. 已知是定义在上的减函数,且对任意都有,则不等式的解集为( ) A. B. C. D. 9.某同学求函数的零点时,用计算器算得部分函数值如表所示: 2 3 2.5 2.75 2.625 2.5625 1.0986 0.512 0.215 0.066 则方程的近似解(精确度0.1)可取为( ) A. 2.52 B. 2.625 C. 2.47 D. 2.75 10.已知函数在上单调递减,则实数的取值范围是( ) A. B. C. D. 11.已知,若,则的值分别为( ) A. B. C. D. 12.对于实数和,定义运算“”:,设函数,若函数的图象与轴恰有两个公共点,则实数的取值范围是( ) A. B. C. D. 二、填空题(本大题共4小题,每小题5分,共20分). 13. 不等式的解集是 . 14. 已知函数f(x)=ln(2x)+3,则f(lg2)+f(lg)= . 15.函数的单调增区间为 . 16. O 1 2 3 4 y 1 t(月) 如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:,有以下叙述: ① 第4个月时,剩留量就会低于; ② 每月减少的有害物质量都相等; ③ 若剩留量为所经过的时间分别是,则. 其中所有正确的叙述是 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本题满分10分) (1)计算:; (2)计算:. 18.(本题满分12分)已知集合A={x|x2-4x+3≤0},B={x|log2x>1}, (1)求A∩B,(∁RB)∪A; (2)集合M={x|1<x<a},若M⊆A,求实数a的取值范围. 19.(本题满分12分)已知关于x的二次函数f(x)=+(2t-1)x+1-2t. (1)求证:对于任意t方程f(x)=1必有实数根; (2)若方程f(x)=0在区间(-1,0)和(0,)内各有一个实数根,求实数t的范围. 20.(本题满分12分)已知函数. (1)判断函数的奇偶性;(2)判断并证明函数的单调性; 21.(本题满分12分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元). (1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式. (2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这 10万元投资,才能使企业获得最大利润,其最大利润约为多少万元(精确到1万元). 22.(本题满分12分)已知指数函数满足,定义域为R的函数是奇函数. (1)确定的解析式; (2)若在上有零点,求的取值范围; (3)若对任意的,不等式f 恒成立,求实数k的取值范围.查看更多