- 2021-06-16 发布 |
- 37.5 KB |
- 15页

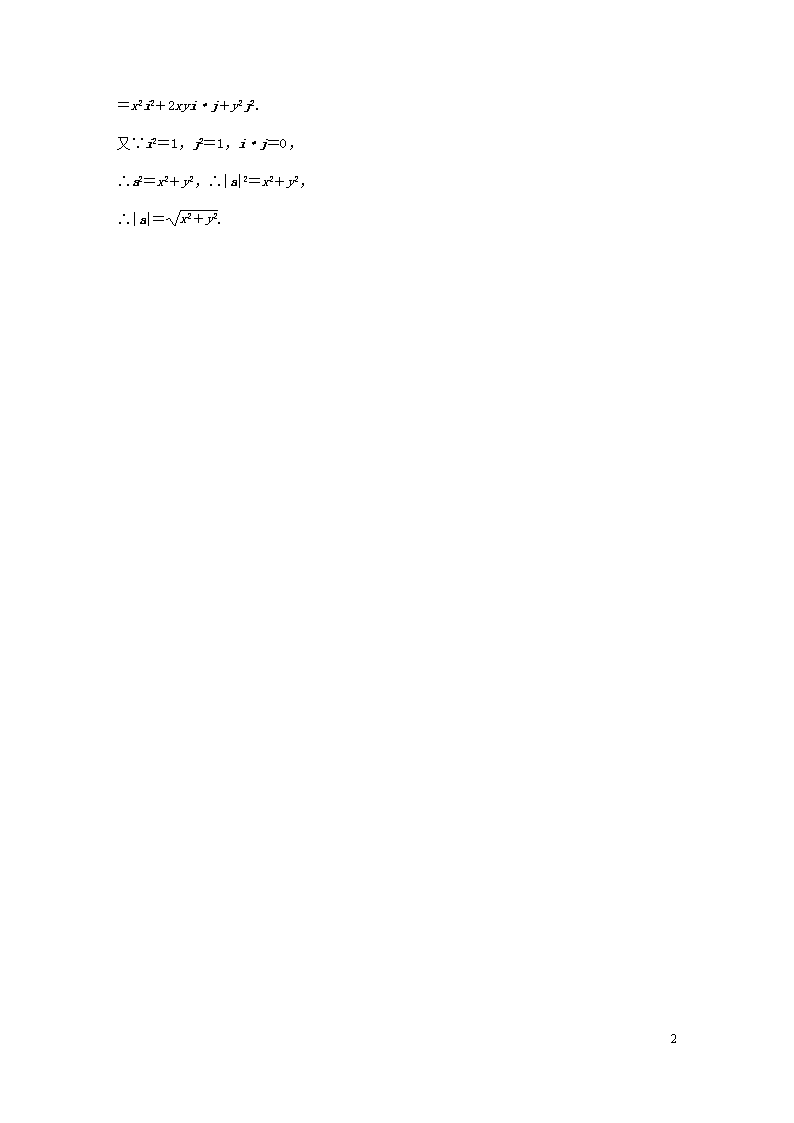

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学 必修4平面向量2.4.2 平面向量数量积的坐标表示、模、夹角
1 2.4.2 平面向量数量积的坐标表示、模、夹角 学习目标 1.理解两个向量数量积坐标表示的推导过程,能运用数量积的坐标表示进行向量 数量积的运算.2.能根据向量的坐标计算向量的模,并推导平面内两点间的距离公式.3.能根 据向量的坐标求向量的夹角及判定两个向量垂直. 知识点一 平面向量数量积的坐标表示 设 i,j 是两个互相垂直且分别与 x 轴、y 轴的正半轴同向的单位向量. 思考 1 i·i,j·j,i·j 分别是多少? 答案 i·i=1×1×cos0=1,j·j=1×1×cos0=1,i·j=0. 思考 2 取 i,j 为坐标平面内的一组基底,设 a=(x1,y1),b=(x2,y2),试将 a,b 用 i,j 表示,并计算 a·b. 答案 ∵a=x1i+y1j,b=x2i+y2j, ∴a·b=(x1i+y1j)·(x2i+y2j)=x1x2i2+(x1y2+x2y1)i·j+y1y2j2=x1x2+y1y2. 思考 3 若 a⊥b,则 a,b 坐标间有何关系? 答案 a⊥b⇔a·b=0⇔x1x2+y1y2=0. 梳理 设向量 a=(x1,y1),b=(x2,y2),a 与 b 的夹角为θ. 数量积 a·b=x1x2+y1y2 向量垂直 a⊥b⇔x1x2+y1y2=0 知识点二 平面向量模的坐标形式及两点间的距离公式 思考 1 若 a=(x,y),试将向量的模|a|用坐标表示. 答案 ∵a=xi+yj,x,y∈R, ∴a2=(xi+yj)2=(xi)2+2xyi·j+(yj)2 =x2i2+2xyi·j+y2j2. 又∵i2=1,j2=1,i·j=0, ∴a2=x2+y2,∴|a|2=x2+y2, ∴|a|= x2+y2. 2 思考 2 若 A(x1,y1),B(x2,y2),如何计算向量AB→的模? 答案 ∵AB→=OB→-OA→ =(x2,y2)-(x1,y1) =(x2-x1,y2-y1), ∴|AB→|= x2-x1 2+ y2-y1 2. 梳理 向量 模长 a=(x,y) |a|= x2+y2 以 A(x1,y1),B(x2,y2)为端点的向量AB→ |AB→|= x2-x1 2+ y2-y1 2 知识点三 平面向量夹角的坐标表示 思考 设 a,b 都是非零向量,a=(x1,y1),b=(x2,y2),θ是 a 与 b 的夹角,那么 cosθ如 何用坐标表示? 答案 cosθ= a·b |a||b| = x1x2+y1y2 x2 1+y2 1 x2 2+y2 2 . 1.若 a=(x1,y1),b=(x2,y2),则 a⊥b⇔x1x2+y1y2=0.( × ) 2.若 a=(x1,y1),b=(x2,y2),则 a⊥b⇔x1y2-x2y1=0.( × ) 3.若两个非零向量的夹角θ满足 cosθ>0,则两向量的夹角θ一定是锐角.( × ) 提示 当两向量同向共线时,cosθ=1>0,但夹角θ=0,不是锐角. 类型一 数量积的坐标运算 例 1 (1)已知 a=(2,-1),b=(1,-1),则(a+2b)·(a-3b)等于( ) A.10 B.-10 C.3 D.-3 3 考点 平面向量数量积的坐标表示与应用 题点 坐标形式下的数量积运算 答案 B 解析 a+2b=(4,-3),a-3b=(-1,2),所以(a+2b)·(a-3b)=4×(-1)+(-3)×2 =-10. (2)如图所示,在矩形 ABCD 中,AB= 2,BC=2,点 E 为 BC 的中点,点 F 在边 CD 上,且DF→= 2FC→,则AE→·BF→的值是________. 考点 平面向量数量积的坐标表示与应用 题点 坐标形式下的数量积运算 答案 4 3 解析 以 A 为原点,AB 所在直线为 x 轴、AD 所在直线为 y 轴建立如图所示平面直角坐标系. ∵AB= 2,BC=2, ∴A(0,0),B( 2,0),C( 2,2),D(0,2), ∵点 E 为 BC 的中点,∴E( 2,1), ∵点 F 在边 CD 上,且DF→=2FC→, ∴F 2 2 3 ,2 .∴AE→=( 2,1),BF→= - 2 3 ,2 , ∴AE→·BF→=-2 3 +2=4 3 . 反思与感悟 数量积坐标运算的技巧 (1)进行数量积运算时,要正确使用公式 a·b=x1x2+y1y2,并能灵活运用以下几个关系: ①|a|2=a·a; ②(a+b)·(a-b)=|a|2-|b|2; ③(a+b)2=|a|2+2a·b+|b|2. 4 (2)在平面几何图形中求数量积,若几何图形规则易建系,一般先建立坐标系,写出相关向量 的坐标,再求数量积. 跟踪训练 1 向量 a=(1,-1),b=(-1,2),则(2a+b)·a 等于( ) A.-1B.0C.1D.2 考点 平面向量数量积的坐标表示与应用 题点 坐标形式下的数量积运算 答案 C 解析 因为 a=(1,-1),b=(-1,2),所以 2a+b=2(1,-1)+(-1,2)=(1,0),则(2a +b)·a=(1,0)·(1,-1)=1,故选 C. 类型二 平面向量的模 例 2 已知平面向量 a=(3,5),b=(-2,1). (1)求 a-2b 及其模的大小; (2)若 c=a-(a·b)b,求|c|. 考点 平面向量模与夹角的坐标表示的应用 题点 利用坐标求向量的模 解 (1)∵a=(3,5),b=(-2,1), ∴a-2b=(3,5)-2(-2,1)=(3+4,5-2)=(7,3), ∴|a-2b|= 72+32= 58. (2)∵a·b=-6+5=-1, ∴c=a+b=(1,6), ∴|c|= 12+62= 37. 反思与感悟 求向量 a=(x,y)的模的常见思路及方法 (1)求模问题一般转化为求模的平方,与向量数量积联系要灵活应用公式 a2=|a|2=x2+y2, 求模时,勿忘记开方. (2)a·a=a2=|a|2 或|a|= a2= x2+y2,此性质可用来求向量的模,可以实现实数运算与向 量运算的相互转化. 跟踪训练 2 已知向量 a=(2,1),a·b=10,|a+b|=5 2,则|b|等于( ) A. 5B. 10C.5D.25 考点 平面向量模与夹角的坐标表示的应用 题点 利用坐标求向量的模 答案 C 解析 ∵a=(2,1),∴a2=5, 又|a+b|=5 2,∴(a+b)2=50, 即 a2+2a·b+b2=50, 5 ∴5+2×10+b2=50,∴b2=25,∴|b|=5. 类型三 平面向量的夹角问题 例 3 (2017·山东枣庄八中月考)已知点 A(3,0),B(0,3),C(cosα,sinα),O(0,0),若|OA→ +OC→|= 13,α∈(0,π),则OB→,OC→的夹角为( ) A.π 2 B.π 4 C.π 3 D.π 6 考点 平面向量夹角的坐标表示与应用 题点 求坐标形式下的向量的夹角 答案 D 解析 因为|OA→+OC→|2=(OA→+OC→)2=OA→2+2OA→·OC→+OC→2=9+6cosα+1=13, 所以 cosα=1 2 , 因为α∈(0,π),所以α=π 3 ,所以 C 1 2 , 3 2 , 所以 cos〈OB→,OC→〉= OB→·OC→ |OB→||OC→| = 3× 3 2 3×1 = 3 2 , 因为 0≤〈OB→,OC→〉≤π,所以〈OB→,OC→〉=π 6 , 所以OB→,OC→的夹角为π 6 ,故选 D. 反思与感悟 利用向量的数量积求两向量夹角的一般步骤 (1)利用向量的坐标求出这两个向量的数量积. (2)利用|a|= x2+y2求两向量的模. (3)代入夹角公式求 cosθ,并根据θ的范围确定θ的值. 跟踪训练 3 已知 a=(1,-1),b=(λ,1),若 a 与 b 的夹角α为钝角,求λ的取值范围. 考点 平面向量夹角的坐标表示与应用 题点 已知坐标形式下的向量夹角求参数 解 ∵a=(1,-1),b=(λ,1), ∴|a|= 2,|b|= 1+λ2,a·b=λ-1. 又∵a,b 的夹角α为钝角, ∴ λ-1<0, 2· 1+λ2≠1-λ, 即 λ<1, λ2+2λ+1≠0. 6 ∴λ<1 且λ≠-1. ∴λ的取值范围是(-∞,-1)∪(-1,1). 类型四 平面向量的垂直问题 例 4 在△ABC 中,AB→=(2,3),AC→=(1,k),若△ABC 是直角三角形,求 k 的值. 考点 向量平行与垂直的坐标表示的应用 题点 已知向量垂直求参数 解 ∵AB→=(2,3),AC→=(1,k), ∴BC→=AC→-AB→=(-1,k-3). 若∠A=90°,则AB→·AC→=2×1+3×k=0,∴k=-2 3 ; 若∠B=90°,则AB→·BC→=2×(-1)+3(k-3)=0, ∴k=11 3 ; 若∠C=90°,则AC→·BC→=1×(-1)+k(k-3)=0, ∴k=3± 13 2 . 故所求 k 的值为-2 3 或11 3 或3± 13 2 . 反思与感悟 利用向量数量积的坐标表示解决垂直问题的实质是把垂直条件代数化,若在关 于三角形的问题中,未明确哪个角是直角时,要分类讨论. 跟踪训练 4 已知 a=(-3,2),b=(-1,0),若向量λa+b 与 a-2b 垂直,则实数λ的值为 ( ) A.1 7 B.-1 7 C.1 6 D.-1 6 考点 向量平行与垂直的坐标表示的应用 题点 已知向量垂直求参数 答案 B 解析 由向量λa+b 与 a-2b 垂直,得 (λa+b)·(a-2b)=0. 因为 a=(-3,2),b=(-1,0), 所以(-3λ-1,2λ)·(-1,2)=0, 即 3λ+1+4λ=0,解得λ=-1 7 . 7 1.已知 a=(3,4),b=(5,12),则 a 与 b 夹角的余弦值为( ) A.63 65 B. 65C. 13 5 D. 13 考点 平面向量夹角的坐标表示与应用 题点 求坐标形式下的向量的夹角 答案 A 解析 |a|= 32+42=5,|b|= 52+122=13. a·b=3×5+4×12=63. 设 a,b 夹角为θ,所以 cosθ= 63 5×13 =63 65 . 2.若向量 a=(x,2),b=(-1,3),a·b=3,则 x 等于( ) A.3B.-3C.5 3 D.-5 3 考点 平面向量数量积的坐标表示与应用 题点 已知数量积求参数 答案 A 解析 a·b=-x+6=3,故 x=3. 3.已知向量 m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ等于( ) A.-4B.-3C.-2D.-1 考点 向量平行与垂直的坐标表示的应用 题点 已知向量垂直求参数 答案 B 解析 因为 m+n=(2λ+3,3),m-n=(-1,-1), 由(m+n)⊥(m-n),可得(m+n)·(m-n)=(2λ+3,3)·(-1,-1)=-2λ-6=0,解得 λ=-3. 4.若平面向量 a=(1,-2)与 b 的夹角是 180°,且|b|=3 5,则 b 等于( ) A.(-3,6) B.(3,-6) C.(6,-3) D.(-6,3) 考点 平面向量数量积的坐标表示与应用 8 题点 已知数量积求向量的坐标 答案 A 解析 由题意设 b=λa=(λ,-2λ)(λ<0), 则|b|= λ2+ -2λ 2= 5|λ|=3 5, 又λ<0,∴λ=-3,故 b=(-3,6). 5.已知 a=(4,3),b=(-1,2). (1)求 a 与 b 的夹角的余弦值; (2)若(a-λb)⊥(2a+b),求实数λ的值. 考点 向量平行与垂直的坐标表示的应用 题点 已知向量垂直求参数 解 (1)∵a·b=4×(-1)+3×2=2, |a|= 42+32=5,|b|= -1 2+22= 5, ∴cos〈a,b〉= a·b |a||b| = 2 5 5 =2 5 25 . (2)∵a-λb=(4+λ,3-2λ),2a+b=(7,8), (a-λb)⊥(2a+b), ∴(a-λb)·(2a+b)=7(4+λ)+8(3-2λ)=0, ∴λ=52 9 . 1.平面向量数量积的定义及其坐标表示,提供了数量积运算的两种不同的途径.准确地把握 这两种途径,根据不同的条件选择不同的途径,可以优化解题过程.同时,平面向量数量积 的两种形式沟通了“数”与“形”转化的桥梁,成为解决距离、角度、垂直等有关问题的有 力工具. 2.应用数量积运算可以解决两向量的垂直、平行、夹角以及长度等几何问题,在学习中要不 断地提高利用向量工具解决数学问题的能力. 3.注意区分两向量平行与垂直的坐标形式,二者不能混淆,可以对比学习、记忆.若 a=(x1, y1),b=(x2,y2),则 a∥b⇔x1y2-x2y1=0,a⊥b⇔x1x2+y1y2=0. 4.事实上应用平面向量的数量积公式解答某些平面向量问题时,向量夹角问题却隐藏了许多 陷阱与误区,常常会出现因模糊“两向量的夹角的概念”和忽视“两向量夹角”的范围,稍 不注意就会带来失误与错误. 9 一、选择题 1.已知 a=(3,-1),b=(1,-2),则 a 与 b 的夹角为( ) A.π 6 B.π 4 C.π 3 D.π 2 考点 平面向量夹角的坐标表示与应用 题点 求坐标形式下的向量的夹角 答案 B 解析 ∵|a|= 10,|b|= 5,a·b=5. ∴cos〈a,b〉= a·b |a||b| = 5 10× 5 = 2 2 . 又∵a,b 的夹角范围为[0,π]. ∴a 与 b 的夹角为π 4 . 2.设向量 a=(2,0),b=(1,1),则下列结论中正确的是( ) A.|a|=|b| B.a·b=0 C.a∥b D.(a-b)⊥b 考点 向量平行与垂直的坐标表示的应用 题点 向量垂直的坐标表示的综合应用 答案 D 解析 a-b=(1,-1),所以(a-b)·b=1-1=0, 所以(a-b)⊥b. 3.已知向量 a=(0,-2 3),b=(1, 3),则向量 a 在 b 方向上的投影为( ) A. 3B.3C.- 3D.-3 考点 平面向量投影的坐标表示与应用 题点 利用坐标求向量的投影 答案 D 解析 向量 a 在 b 方向上的投影为a·b |b| =-6 2 =-3.故选 D. 4.已知向量 a=(1,n),b=(-1,n),若 2a-b 与 b 垂直,则|a|等于( ) A.1B. 2C.2D.4 考点 平面向量模与夹角的坐标表示的应用 题点 利用坐标求向量的模 10 答案 C 解析 ∵(2a-b)·b=2a·b-|b|2 =2(-1+n2)-(1+n2)=n2-3=0, ∴n2=3,∴|a|= 12+n2=2. 5.若 a=(2,-3),则与向量 a 垂直的单位向量的坐标为( ) A.(3,2) B. 3 13 13 ,2 13 13 C. 3 13 13 ,2 13 13 或 -3 13 13 ,-2 13 13 D.以上都不对 考点 向量平行与垂直的坐标表示的应用 题点 向量垂直的坐标表示的综合应用 答案 C 解析 设与 a 垂直单位向量的坐标为(x,y), ∵(x,y)是单位向量的坐标形式, ∴ x2+y2=1,即 x2+y2=1,① 又∵(x,y)表示的向量垂直于 a, ∴2x-3y=0,② 由①②得 x=3 13 13 , y=2 13 13 或 x=-3 13 13 , y=-2 13 13 . 6.已知 a=(1,1),b=(0,-2),且 ka-b 与 a+b 的夹角为 120°,则 k 等于( ) A.-1+ 3 B.-2 C.-1± 3 D.1 考点 平面向量夹角的坐标表示与应用 题点 已知坐标形式下的向量夹角求参数 答案 C 解析 ∵|ka-b|= k2+ k+2 2, |a+b|= 12+ -1 2= 2, ∴(ka-b)·(a+b)=(k,k+2)·(1,-1)=k-k-2=-2, 又 ka-b 与 a+b 的夹角为 120°, ∴cos120°= ka-b· a+b |ka-b||a+b| , 11 即-1 2 = -2 2× k2+ k+2 2 , 化简并整理,得 k2+2k-2=0,解得 k=-1± 3. 7.已知OA→=(-2,1),OB→=(0,2)且AC→∥OB→,BC→⊥AB→,则点 C 的坐标是( ) A.(2,6) B.(-2,-6) C.(2,-6) D.(-2,6) 考点 向量平行与垂直的坐标表示的应用 题点 向量平行与垂直的坐标表示的综合应用 答案 D 解析 设 C(x,y),则AC→=(x+2,y-1), BC→=(x,y-2),AB→=(2,1), ∵AC→∥OB→,∴2(x+2)=0,① ∵BC→⊥AB→,∴2x+y-2=0,② 由①②可得 x=-2, y=6, ∴C(-2,6). 二、填空题 8.已知平面向量 a=(2,4),b=(1,-2),若 c=a-(a·b)b,则|c|=________. 考点 平面向量模与夹角的坐标表示的应用 题点 利用坐标求向量的模 答案 8 2 解析 由题意可得 a·b=2×1+4×(-2)=-6, ∴c=a-(a·b)b=a+6b=(2,4)+6(1,-2)=(8,-8), ∴|c|= 82+ -8 2=8 2. 9.已知 a=(3, 3),b=(1,0),则(a-2b)·b=________. 考点 平面向量数量积的坐标表示与应用 题点 坐标形式下的数量积运算 答案 1 解析 a-2b=(1, 3), (a-2b)·b=1×1+ 3×0=1. 10.设 m=(a,b),n=(c,d),规定两向量 m,n 之间的一个运算“⊗ ”为 m⊗ n=(ac-bd, ad+bc),若已知 p=(1,2),p⊗ q=(-4,-3),则 q 的坐标为________. 考点 平面向量数量积的坐标表示与应用 题点 已知数量积求向量的坐标 12 答案 (-2,1) 解析 设 q=(x,y),则 p⊗ q=(x-2y,y+2x)=(-4,-3). ∴ x-2y=-4, y+2x=-3, ∴ x=-2, y=1. ∴q=(-2,1). 11.(2017·广东揭阳惠来一中、揭东一中联考)已知向量OA→=(1,7),OB→=(5,1)(O 为坐标原 点),设 M 为直线 y=1 2 x 上的一点,那么MA→·MB→的最小值是________. 考点 平面向量数量积的坐标表示与应用 题点 坐标形式下的数量积运算 答案 -8 解析 设 M x,1 2 x , 则MA→= 1-x,7-1 2 x ,MB→= 5-x,1-1 2 x , MA→·MB→=(1-x)(5-x)+ 7-1 2 x 1-1 2 x =5 4 (x-4)2-8. 所以当 x=4 时,MA→·MB→取得最小值-8. 三、解答题 12.已知 a,b,c 是同一平面内的三个向量,其中 a=(1,2). (1)若|c|=2 5,且 c 与 a 方向相反,求 c 的坐标; (2)若|b|= 5 2 ,且 a+2b 与 2a-b 垂直,求 a 与 b 的夹角θ. 考点 向量平行与垂直的坐标表示的应用 题点 向量平行与垂直的坐标表示的综合应用 解 (1)设 c=(x,y),由 c∥a 及|c|=2 5, 可得 1·y-2·x=0, x2+y2=20, 所以 x=2, y=4 或 x=-2, y=-4, 因为 c 与 a 方向相反,所以 c=(-2,-4). (2)因为(a+2b)⊥(2a-b), 所以(a+2b)·(2a-b)=0,即 2a2+3a·b-2b2=0, 所以 2|a|2+3a·b-2|b|2=0, 13 所以 2×5+3a·b-2×5 4 =0, 所以 a·b=-5 2 .所以 cosθ= a·b |a||b| =-1. 又因为θ∈[0,π],所以θ=π. 13.平面内有向量OA→=(1,7),OB→=(5,1),OP→=(2,1),点 Q 为直线 OP 上的一个动点. (1)当QA→·QB→取最小值时,求OQ→的坐标; (2)当点 Q 满足(1)的条件和结论时,求 cos∠AQB 的值. 考点 向量平行与垂直的坐标表示的应用 题点 向量平行与垂直的坐标表示的综合应用 解 (1)设OQ→=(x,y), ∵Q 在直线 OP 上,∴向量OQ→与OP→共线. 又OP→=(2,1),∴x-2y=0,∴x=2y, ∴OQ→=(2y,y). 又QA→=OA→-OQ→=(1-2y,7-y), QB→=OB→-OQ→=(5-2y,1-y), ∴QA→·QB→=(1-2y)(5-2y)+(7-y)(1-y) =5y2-20y+12=5(y-2)2-8. 故当 y=2 时,QA→·QB→有最小值-8,此时OQ→=(4,2). (2)由(1)知QA→=(-3,5),QB→=(1,-1), QA→·QB→=-8,|QA→|= 34,|QB→|= 2, ∴cos∠AQB= QA→·QB→ |QA→|·|QB→| = -8 34× 2 =-4 17 17 . 四、探究与拓展 14.已知向量 a=(1,1),b=(1,m),其中 m 为实数,则当 a 与 b 的夹角在 0,π 12 内变动时, 实数 m 的取值范围是( ) A.(0,1) B. 3 3 , 3 C. 3 3 ,1 ∪(1, 3) D.(1, 3) 14 考点 平面向量夹角的坐标表示与应用 题点 已知坐标形式下的向量夹角求参数 答案 C 解析 如图,作OA→=a,则 A(1,1). 作OB1 →,OB2 →, 使∠AOB1=∠AOB2=π 12 , 则∠B1Ox=π 4 -π 12 =π 6 , ∠B2Ox=π 4 +π 12 =π 3 , 故 B1 1, 3 3 ,B2(1, 3). 又 a 与 b 的夹角不为 0,故 m≠1. 由图可知实数 m 的取值范围是 3 3 ,1 ∪(1, 3). 15.已知OA→=(4,0),OB→=(2,2 3),OC→=(1-λ)OA→+λOB→(λ2≠λ). (1)求OA→·OB→及OA→在OB→上的投影; (2)证明 A,B,C 三点共线,且当AB→=BC→时,求λ的值; (3)求|OC→|的最小值. 考点 平面向量模与夹角的坐标表示的应用 题点 平面向量模的坐标表示的应用 解 (1)OA→·OB→=8,设OA→与OB→的夹角为θ, 则 cosθ= OA→·OB→ |OA→||OB→| = 8 4×4 =1 2 , ∴OA→在OB→上的投影为|OA→|cosθ=4×1 2 =2. (2)AB→=OB→-OA→=(-2,2 3),BC→=OC→-OB→ 15 =(1-λ)OA→-(1-λ)OB→=(λ-1)AB→, 又因为BC→与AB→有公共点 B,所以 A,B,C 三点共线. 当AB→=BC→时,λ-1=1,所以λ=2. (3)|OC→|2=(1-λ)2OA→2+2λ(1-λ)OA→·OB→+λ2OB→2=16λ2-16λ+16=16 λ-1 2 2+12, ∴当λ=1 2 时,|OC→|取最小值 2 3.查看更多