- 2021-06-16 发布 |
- 37.5 KB |
- 48页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习人教A版8-7立体几何中的向量方法学案
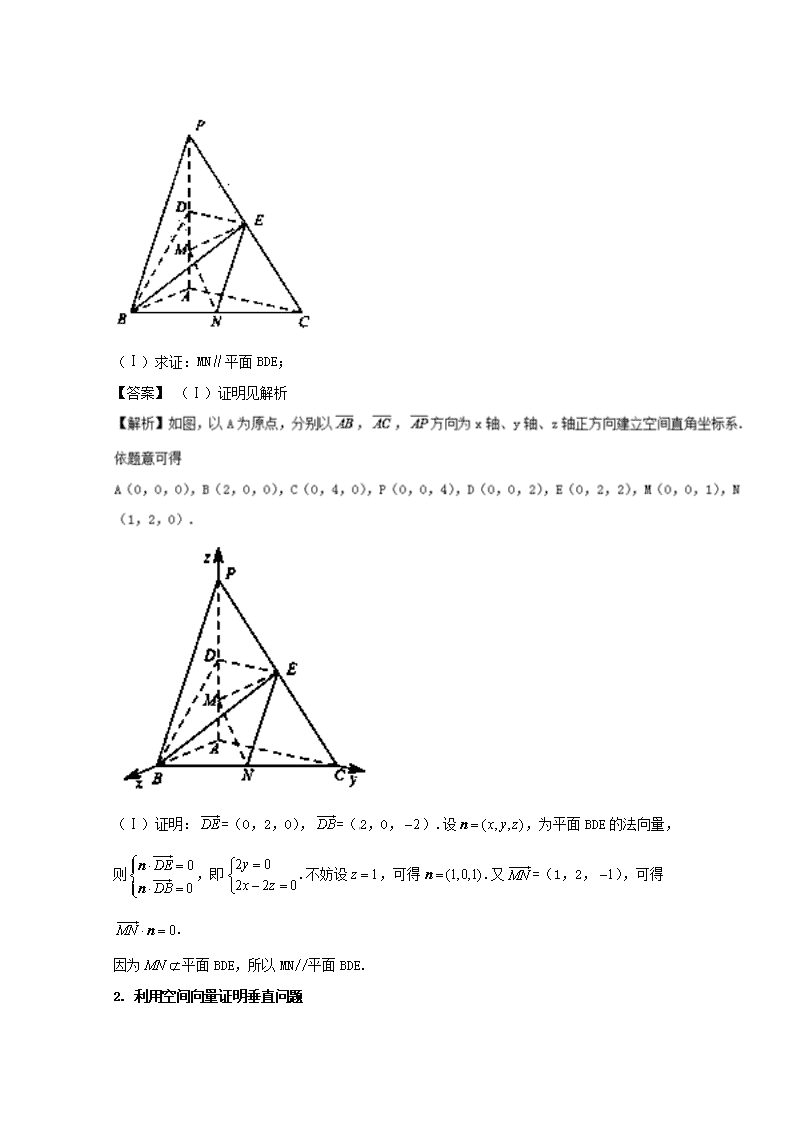
第07节 立体几何中的向量方法 【考纲解读】 考 点 考纲内容 5年统计 分析预测 立体几何中的向量方法 (1)理解直线的方向向量与平面的法向量. (2)能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系. (3)能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理). 2015•浙江文18;理17; 2016•浙江理17; 1.以几何体为载体,综合考查平行或垂直关系证明,以及角与距离的计算. 2.利用几何法证明平行、垂直关系,利用空间向量方法求角或距离. 3.备考重点: (1) 掌握空间向量的坐标运算; (2)掌握角与距离的计算方法. 【知识清单】 1. 利用空间向量证明平行问题 1.直线的方向向量与平面的法向量的确定 ①直线的方向向量:l是空间一直线,A,B是直线l上任意两点,则称为直线l的方向向量,与平行的任意非零向量也是直线l的方向向量. ②平面的法向量可利用方程组求出:设a,b是平面α内两不共线向量,n为平面α的法向量,则求法向量的方程组为 2.用向量证明空间中的平行关系 ①设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合)⇔v1∥v2. ②设直线l的方向向量为v,与平面α共面的两个不共线向量v1和v2,则l∥α或l⊂α⇔存在两个实数x,y,使v=xv1+yv2. ③设直线l的方向向量为v,平面α的法向量为u,则l∥α或l⊂α⇔v⊥u. ④设平面α和β的法向量分别为u1,u2,则α∥β⇔u1∥u2. 对点练习: 【选自2017天津,理17】如图,在三棱锥P-ABC中,PA⊥底面ABC,.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2. (Ⅰ)求证:MN∥平面BDE; 【答案】 (Ⅰ)证明见解析 (Ⅰ)证明:=(0,2,0),=(2,0,).设,为平面BDE的法向量, 则,即.不妨设,可得.又=(1,2,),可得. 因为平面BDE,所以MN//平面BDE. 2. 利用空间向量证明垂直问题 1. 用向量证明空间中的垂直关系 ①设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2⇔v1⊥v2⇔v1·v2=0. ②设直线l的方向向量为v,平面α的法向量为u,则l⊥α⇔v∥u. ③设平面α和β的法向量分别为u1和u2,则α⊥β⇔u1⊥u2⇔u1·u2=0. 2.共线与垂直的坐标表示 设a=(a1,a2,a3),b=(b1,b2,b3),则a∥b⇔a=λb⇔a1=λb1,a2=λb2,a3=λb3(λ∈R), a⊥b⇔a·b=0⇔a1b1+a2b2+a3b3=0(a,b均为非零向量). 对点练习: 【河南省信阳市期末】已知梯形如下图所示,其中,,为线段的中点,四边形为正方形,现沿进行折叠,使得平面平面,得到如图所示的几何体.已知当点满足时,平面平面,则的值为( ) A. B. C. D. 【答案】C 则,,设平面的法向量为,则由得,取,平面的法向量为,则由得,取, 因为平面平面,所以,解得.故选C. 3. 异面直线所成的角 1.两条异面直线所成的角 ①定义:设a,b是两条异面直线,过空间任一点O作直线a′∥a,b′∥b,则a′与b′所夹的锐角或直角叫做a与b所成的角. ②范围:两异面直线所成角θ的取值范围是. ③向量求法:设直线a,b的方向向量为a,b,其夹角为φ,则有. 对点练习: 【2017课标II,理10】已知直三棱柱中,,,,则异面直线与所成角的余弦值为( ) A. B. C. D. 【答案】C 【解析】如图所示,补成四棱柱 , 4. 直线与平面所成角 1.直线和平面所成角的求法:如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sin φ=|cos θ|=. 对点练习: 【2017浙江,19】(本题满分15分)如图,已知四棱锥P–ABCD,△PAD是以AD为斜边的等腰直角三角形,,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点. (Ⅰ)证明:平面PAB; (Ⅱ)求直线CE与平面PBC所成角的正弦值. 【答案】(Ⅰ)见解析;(Ⅱ). 【解析】 试题解析: MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角. 设CD=1. 在△PCD中,由PC=2,CD=1,PD=得CE=, 在△PBN中,由PN=BN=1,PB=得QH=, 在Rt△MQH中,QH=,MQ=, 所以sin∠QMH=, 所以直线CE与平面PBC所成角的正弦值是. 5.二面角 1.求二面角的大小 (1)如图1,AB、CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=〈,〉. (2)如图2、3,分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小(或). 对点练习: 【2017江苏,22】 如图, 在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=, . (1)求异面直线A1B与AC1所成角的余弦值; (2)求二面角B-A1D-A的正弦值. 【答案】(1)(2) 6 .利用向量求空间距离 1.空间向量的坐标表示及运算 (1)数量积的坐标运算 设a=(a1,a2,a3),b=(b1,b2,b3), 则①a±b=(a1±b1,a2±b2,a3±b3); ②λa=(λa1,λa2,λa3); ③a·b=a1b1+a2b2+a3b3. (2)共线与垂直的坐标表示 设a=(a1,a2,a3),b=(b1,b2,b3), 则a∥b⇔a=λb⇔a1=λb1,a2=λb2,a3=λb3(λ∈R), a⊥b⇔a·b=0⇔a1b1+a2b2+a3b3=0(a,b均为非零向量). (3)模、夹角和距离公式 设a=(a1,a2,a3),b=(b1,b2,b3), 则|a|==, cos〈a,b〉==. 设A(a1,b1,c1),B(a2,b2,c2), 则. 2. 点面距的求法 如图,设AB为平面α的一条斜线段,n为平面α的法向量,则B到平面α的距离d=. 对点练习: 设正方体的棱长为2,则点到平面的距离是( ) A. B. C. D. 【答案】D 【考点深度剖析】 利用空间向量证明平行或垂直是高考的热点,内容以解答题中的一问为主,主要围绕考查空间直角坐标系的建立、空间向量的坐标运算能力和分析解决问题的能力命制试题,以多面体为载体、证明线面(面面)的平行(垂直)关系是主要命题方向.空间的角与距离的计算(特别是角的计算)是高考热点,一般以大题的条件或一小问形式呈现,考查用向量方法解决立体几何问题,将空间几何元素之间的位置关系转化为数量关系,并通过计算解决立体几何问题.距离问题往往在与有关面积、体积的计算中加以考查.此类问题往往属于“证算并重”题,即第一问用几何法证明平行关系或垂直关系,第二问则通过建立空间直角坐标系,利用空间向量方法进一步求角或距离.浙江卷对空间向量方法考题较少,较为注重几何法的考查. 【重点难点突破】 考点1 利用空间向量证明平行问题 【1-1】如图所示,在正方体ABCDA1B1C1D1中,M、N分别是C1C、B1C1的中点.求证:MN∥平面A1BD. 【答案】MN∥平面A1BD. 则M,N,D(0,0,0),A1(1,0,1),B(1,1,0), 于是=, 设平面A1BD的法向量是n=(x,y,z). 则n·=0,且n·=0,得 取x=1,得y=-1,z=-1.∴n=(1,-1,-1). 又·n=·(1,-1,-1)=0, ∴⊥n,又MN⊄平面A1BD, ∴MN∥平面A1BD. 法二 =-=-=(-)=, ∴∥,又∵MN与DA1不共线,∴MN∥DA1, 又∵MN⊄平面A1BD,A1D⊂平面A1BD, ∴MN∥平面A1BD. 【1-2】(1)如图所示,在长方体OAEB-O1A1E1B1中,|OA|=3,|OB|=4,|OO1|=2,点P在棱AA1上,且|AP|=2|PA1|,点S在棱BB1上,且|SB1|=2|BS|,点Q、R分别是O1B1、AE的中点,求证:PQ∥RS. 【答案】PQ∥RS 方法二:设,则 , . ,//.又∵R∉PQ,∴PQ∥RS. 【领悟技法】 证明直线与平面平行,只须证明直线的方向向量与平面的法向量的数量积为零,或证直线的方向向量与平面内的不共线的两个向量共面,然后说明直线在平面外即可.这样就把几何的证明问题转化为了数量的计算问题. 【触类旁通】 【变式一】【湖北卷】如图,在棱长为2的正方体中,分别是棱的中点,点分别在棱,上移动,且. (1) 当时,证明:直线平面. 【答案】直线平面. (1)证明:当时,,因为, 所以,即, 而平面,且平面, 故直线平面. 考点2 利用空间向量证明垂直问题 【2-1】【2017届江西省上饶市二模】如图,在长方体中, ,点为线段上的动点(包含线段端点),则下列结论正确的__________. ①当时, 平面; ②当时, 平面; ③的最大值为; ④的最小值为. 【答案】①② 解得,由于,所以平面成立.对于②,当时,即,解得,由可知平面成立.对于③,设,即,解得,由,其分子化简得,当时, ,故的最大值可以为钝角,③错误.对于④,根据③计算的数据, , ,在对称轴,即时取得最小值为,故④错误. 【2-2】如图所示,在棱长为1的正方体OABCO1A1B1C1中,E,F分别是棱AB,BC上的动点,且AE=BF=x,其中0≤x≤1,以O为原点建立空间直角坐标系Oxyz. (1)求证A1F⊥C1E; (2)若A1,E,F,C1四点共面,求证:=+. 【答案】(1)A1F⊥C1E;(2)=+. (2)=(-x,1,-1),=(-1,1,0),=(0,x,-1), 设=λ+μ,解得λ=,μ=1. ∴=+. 【领悟技法】 1. 证明直线与直线垂直,只需要证明两条直线的方向向量垂直,而直线与平面垂直,平面与平面垂直可转化为直线与直线垂直证明. 2.要证明两线垂直,需转化为两线对应的向量垂直,进一步转化为证明两向量的数量积为零,这是证明两线垂直的基本方法,线线垂直是证明线面垂直,面面垂直的基础. 3.证明线面垂直,可利用判定定理.如本题解法. 4.用向量证明两个平面垂直,关键是求出两个平面的法向量,把证明面面垂直转化为法向量垂直. 【触类旁通】 【变式一】【广东省广州市普通高中毕业班综合测试】如图5,在棱长为的正方体中,点是棱的中点,点在棱上,且满足. (1)求证:; (2)在棱上确定一点,使、、、四点共面,并求此时的长. 【答案】(1);(2)故当时,、、、四点共面. 所以,,因为, 所以,所以; (2)设,因为平面平面, 平面平面,平面平面,所以, 所以存在实数,使得, 因为,,所以, 所以,,所以, 故当时,、、、四点共面. 考点3 异面直线所成的角 【3-1】【2017届浙江省嘉兴一中、杭州高级中学、宁波效实中学等高三下五校联考】正方体中,点在上运动(包括端点),则与所成角的取值范围是( ) A. B. C. D. 【答案】D 【3-2】长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( ) A. B. C. D. 【答案】 B 【解析】建立坐标系如图,则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2). , . 所以异面直线BC1与AE所成角的余弦值为. 【领悟技法】 1.求一对异面直线所成角:一是按定义平移转化为两相交直线的夹角;二是在异面直线上各取一向量,转化为两向量的夹角或其补角,无论哪种求法,都应注意角的范围的限定. 2. 利用直线的方向向量的夹角求异面直线的夹角时,注意区别:当异面直线的方向向量的夹角为锐角或直角时,就是此异面直线所成的角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直线所成的角. 【触类旁通】 【变式一】【2017届安徽省江淮十校高三下第三次联考】如图,正四面体中, 、分别是棱和的中点,则直线和所成的角的余弦值为( ) A. B. C. D. 【答案】B 利用空间向量求解余弦值有: . ∴异面直线AE与CF所成角的余弦值为 . 考点4 直线与平面所成角 【4-1】如图,在长方体中,,,、分别是、的中点.证明、、、四点共面,并求直线与平面所成的角的正弦值大小. 【答案】 【解析】解:如图,以为原点建立空间直角坐标系,可得有关点的坐标为、、、、、. 因为,, 所以,因此直线与共面, 即、、、共面. 因此直线与平面所成的角的正弦值大小为. 【4-2】如图,长方体中,,,,点,分别在,上,.过点,的平面与此长方体的面相交,交线围成一个正方形. D D1 C1 A1 E F A B C B1 (Ⅰ)在图中画出这个正方形(不必说出画法和理由); (Ⅱ)求直线与平面所成角的正弦值. 【答案】(Ⅰ)见解析;(Ⅱ). ,,.设是平面的法向量,则即所以可取.又,故.所以直线与平面所成角的正弦值为. 【领悟技法】 1.利用向量法求线面角的方法 (1)分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角); (2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角(钝角时取其补角),取其余角就是斜线和平面所成的角. 【触类旁通】 【变式一】【2017届湖北武汉市蔡甸区汉阳一中三模】如图,三棱柱中, , , 分别为棱的中点. (1)在平面内过点作平面交于点,并写出作图步骤,但不要求证明. (2)若侧面侧面,求直线与平面所成角的正弦值. 【答案】(1)见解析(2) 试题解析: (1)如图,在平面内,过点作交于点,连结,在中,作交于点,连结并延长交于点,则为所求作直线. (2)连结,∵,∴为正三角形. ∵为的中点,∴, 又∵侧面侧面,且面面, 平面,∴平面, 在平面内过点作交于点, 分别以的方向为轴, 轴, 轴的正方向,建立如图所示的空间直角坐标系,则, . ∵为的中点,∴点的坐标为, ∴. ∵,∴,∴, 设平面的法向量为, 由得, 令,得,所以平面的一个法向量为. 设直线与平面所成角为, 则, 即直线与平面所成角的正弦值为. 考点5 二面角 【5-1】【2017课标1,理18】如图,在四棱锥P-ABCD中,AB//CD,且. (1)证明:平面PAB⊥平面PAD; (2)若PA=PD=AB=DC,,求二面角A-PB-C的余弦值. 【解析】 试题解析:(1)由已知,得AB⊥AP,CD⊥PD. 由于AB∥CD ,故AB⊥PD ,从而AB⊥平面PAD. 又AB 平面PAB,所以平面PAB⊥平面PAD. 由(1)及已知可得,,,. 所以,,,. 设是平面的法向量,则 ,即, 可取. 设是平面的法向量,则 ,即, 可取. 则, 所以二面角的余弦值为. 【5-2】【2017课标II,理19】如图,四棱锥P-ABCD中,侧面PAD为等比三角形且垂直于底面ABCD, E是PD的中点。 (1)证明:直线 平面PAB; (2)点M在棱PC 上,且直线BM与底面ABCD所成角为 ,求二面角的余弦值。 【答案】(1)证明略; (2) 。 【解析】 试题解析: (1)取的中点,连结,。 因为是的中点,所以∥,,由得∥,又,所以。四边形为平行四边形,∥。 又平面,平面,故平面。 (2)由已知得,以A为坐标原点,的方向为x轴正方向,为单位长, 建立如图所示的空间直角坐标系, 则,,,,,, 设则, 因为BM与底面ABCD所成的角为45°,而是底面ABCD的法向量, 所以, , 即。 ① 又M在棱PC上,设,则 。 ② 【领悟技法】 求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角. 【触类旁通】 【变式一】【2017山东,理17】如图,几何体是圆柱的一部分,它是由矩形(及其内部)以边所在直线为旋转轴旋转得到的,是的中点. (Ⅰ)设是上的一点,且,求的大小; (Ⅱ)当,,求二面角的大小. 【答案】(Ⅰ).(Ⅱ). 思路二: 以为坐标原点,分别以,,所在的直线为,,轴,建立如图所示的空间直角坐标系. 写出相关点的坐标,求平面的一个法向量,平面的一个法向量 计算即得. (Ⅱ)解法一: 取的中点,连接,,. 因为, 所以四边形为菱形, 所以. 取中点,连接,,. 则,, 所以为所求二面角的平面角. 又,所以. 在中,由于, 由余弦定理得, 所以,因此为等边三角形, 故所求的角为. 解法二: 以为坐标原点,分别以,,所在的直线为,,轴,建立如图所示的空间直角坐标系. 因此所求的角为. 考点6 利用向量求空间距离 【6-1】在三棱锥SABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点,如图所示,求点B到平面CMN的距离. 【答案】. 则B(0,2,0),C(-2,0,0),S(0,0,2), M(1,,0),N(0,,). ∴=(3,,0),=(-1,0,), =(-1,,0). 设n=(x,y,z)为平面CMN的一个法向量, 则取z=1, 则x=,y=-,∴n=(,-,1). ∴点B到平面CMN的距离 d==. 【6-2】如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2. (1)求点A到平面MBC的距离; (2)求平面ACM与平面BCD所成二面角的正弦值. 【答案】(1) ;(2). (1)设n=(x,y,z)是平面MBC的法向量,则=(1,,0), =(0,,), 由n⊥得x+y=0;由n⊥得y+z=0. 取n=(,-1,1),=(0,0,2),则 d===. (2)=(-1,0,),=(-1,-,2). 设平面ACM的法向量为n1=(x,y,z), 由n1⊥,n1⊥得 解得x=z,y=z,取n1=(,1,1). 又平面BCD的法向量为n2=(0,0,1). 所以cos〈n1,n2〉==. 设所求二面角为θ,则sin θ=. 【领悟技法】 点到平面的距离,利用向量法求解比较简单,它的理论基础仍出于几何法,如本题,事实上,作BH⊥平面CMN于H.由=+及·n=n·,得|·n|=|n·|=||·|n|,所以||=,即d=. 【触类旁通】 【变式一】设正方体ABCD-A1B1C1D1的棱长为2,则点D1到平面A1BD的距离是( ) A. B. C. D. 【答案】D 【解析】如图建立空间直角坐标系,则D1(0,0,2),A1(2,0,2),D(0,0,0),B(2,2,0),∴, 【变式二】在正方体中,为的中点,则异面直线和间的距离 . 【答案】 【解析】设正方体棱长为,以为原点,建立如图所示的空间直角坐标系,则,,设和公垂线段上的向量为,则,即,,,又,,所以异面直线和间的距离为. 【易错试题常警惕】 易错典例1.已知正三棱柱ABC—A1B1C1中,AB=2,AA1=,点D为AC的中点,点E在线段 AA1上. (1)当AE∶EA1=1∶2时,求证DE⊥BC1; (2)是否存在点E,使二面角D—BE—A等于60,若存在求AE的长;若不存在,请说明理由. 易错分析:利用空间向量解决存在性问题时,容易出现解题不规范的情况. (2)假设存在点E满足条件,设AE=h. 取A1C1的中点D1,连结DD1,则DD1⊥平面ABC,所以DD1⊥AD,DD1⊥BD, 分别以DA,DB,DD1所在直线为x,y,z轴建立空间直角坐标系D—xyz,则A(1,0,0),B(0,,0),E(1,0,h),所以=(0,,0),=(1,0,h),=(-1,,0),=(0,0,h), 设平面DBE的一个法向量为n1=(x1,y1,z1), 则,令z1=1,得n1=(-h,0,1), 同理,平面ABE的一个法向量为n2=(x2,y2,z2), 则,令y2=1,得 n2=(,1,0). ∴cos〈n1,n2〉==cos 60°=. 解得h=<, 故存在点E,当AE=时,二面角D—BE—A等于60°. 温馨提醒: 1.对于存在性问题,一般先假设存在,若能求出符合条件的解,则存在,若不能求出符合条件的解,则不存在.2.利用空间向量的方法解立体几何中开放性问题,可以化繁为简,化难为易,降低了思维难度. 【学科素养提升之思想方法篇】 化“生”为“熟”——转化与化归的思想方法 1.转化与化归的思想方法是数学中最基本的思想方法,数学中一切问题的解决(当然包括解题)都离不开转化与化归,数形结合思想体现了数与形的相互转化;函数与方程思想体现了函数、方程、不等式间的相互转化;分类讨论思想体现了局部与整体的相互转化,以上三种思想方法都是转化与化归思想的具体体现。各种变换方法、分析法、反证法、待定系数法、构造法等都是转化的手段。所以说,转化与化归是数学思想方法的灵魂. 2. 转化包括等价转化和非等价转化,非等价转化又分为强化转化和弱化转化 等价转化要求在转化过程中的前因后果既是充分的又是必要的,这样的转化能保证转化的结果仍为原问题所需要的结果,非等价转化其过程则是充分的或必要的,这样的转化能给人带来思维的启迪,找到解决问题的突破口,非等价变形要对所得结论进行必要的修改. 非等价转化(强化转化和弱化转化)在思维上带有跳跃性,是难点,在压轴题的解答中常常用到,一定要特别重视! 3.转化与化归的原则 (1)熟悉化原则:将不熟悉和难解的问题转化为熟知的易解的或已经解决的问题; (2)直观化原则:将抽象的问题转化为具体的直观的问题; (3)简单化原则:将复杂的问题转化为简单的问题,将一般性的问题转化为直观的特殊的问题;将实际问题转化为数学问题,使问题便与解决. (4)正难则反原则:若过正面问题难以解决,可考虑问题的反面,从问题的反面寻求突破的途径; (5)低维度原则:将高维度问题转化成低维度问题. 4.转化与化归的基本类型 (1) 正与反、一般与特殊的转化; (2) 常量与变量的转化; (3) 数与形的转化; (4) 数学各分支之间的转化; (5) 相等与不相等之间的转化; (6) 实际问题与数学模型的转化. 5.常见的转化方法 (1)直接转化法:把原问题直接转化为基本定理、基本公式或基本图形问题; (2)换元法:运用“换元”把非标准形式的方程、不等式、函数转化为容易解决的基本问题; (3)参数法:引进参数,使原问题的变换具有灵活性,易于转化; (4)构造法:“构造”一个合适的数学模型,把问题变为易于解决的问题; (5)坐标法:以坐标系为工具,用代数方法解决解析几何问题,是转化方法的一种重要途径; (6)类比法:运用类比推理,猜测问题的结论,易于确定转化的途径; (7)特殊化方法:把原问题的形式向特殊化形式转化,并证明特殊化后的结论适合原问题; (8)一般化方法:若原问题是某个一般化形式问题的特殊形式且有较难解决,可将问题通过一般化的途径进行转化; (9)等价问题法:把原问题转化为一个易于解决的等价命题,达到转化目的; (10)补集法:(正难则反)若过正面问题难以解决,可将问题的结果看作集合A,而把包含该问题的整体问题的结果类比为全集U,通过解决全集U及补集获得原问题的解决. 立体几何中的转化与化归,主要利用直接转化法或坐标法,将空间问题转化成平面问题、将几何问题转化成代数问题加以解决. 【典例1】【2017北京,理16】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=,AB=4. (I)求证:M为PB的中点; (II)求二面角B-PD-A的大小; (III)求直线MC与平面BDP所成角的正弦值. 【答案】(Ⅰ)详见解析:(Ⅱ) ;(Ⅲ) 【解析】 (III)由题意知,,. 设直线与平面所成角为,则. 所以直线与平面所成角的正弦值为. 【典例2】【云南大理州宾川县第四高级中学】在边长是2的正方体-中,分别为 的中点. 应用空间向量方法求解下列问题. x z y (1)求EF的长 (2)证明:平面; (3)证明: 平面. 【答案】(1) (2)根据题意,关键是能根据向量法来得到即可。 (3)对于题目中,则可以根据线面垂直的判定定理来的得到. 【解析】 试题分析:解(1)如图建立空间直角坐标系 x z y 4分 (2) 而 平面 8分 (3) 又 平面. 12分查看更多