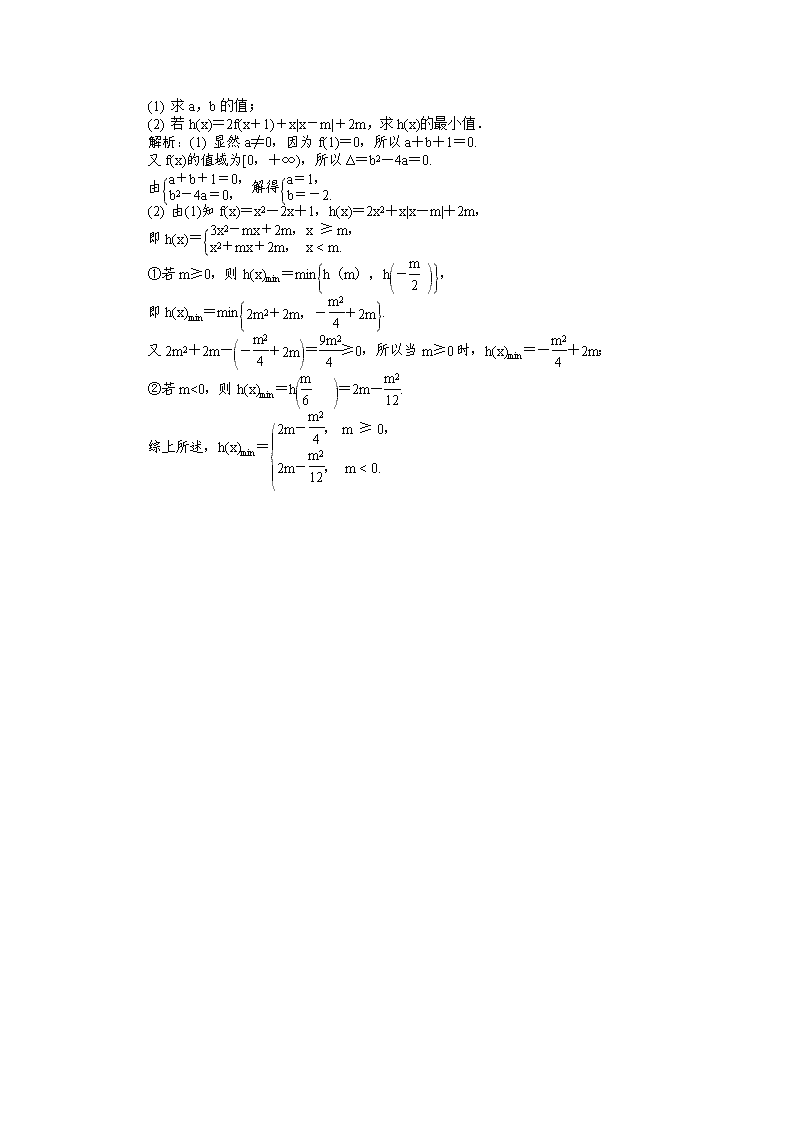【数学】2020届一轮复习人教A版第9课二次函数作业(江苏专用)
随堂巩固训练(9)
1. 若二次函数f(x)=ax2+bx+c图象的顶点坐标为(2,-1),与y轴的交点坐标为(0,11),则a,b,c的值为__3,-12,11__.
解析:由题意得解得故a,b,c的值分别为3,-12,11.
2. 函数f(x)=x2-2x-2(x∈[-2,2])的最小值是__-3__.
解析:因为f(x)=x2-2x-2=(x-1)2-3,所以函数f(x)在区间[-2,1]上单调递减,在区间[1,2]上单调递增,所以f(x)min=f(1)=1-2-2=-3.
3. 如果函数f(x)=x2+px+q对任意的x均有f(1+x)=f(1-x)成立,那么f(0)、f(-1)、f(1)从小到大的顺序为__f(1)
0,c=1,a+a2+b+c=0,所以b=-(a2+a)-1=--.因为a>0,所以b<-1,故实数b的取值范围为(-∞,-1).
10. 函数y=(x+1)(x+2)(x+3)(x+4)+5在区间[-3,3]上的最小值为__4__.
解析:因为y=(x+1)(x+2)(x+3)(x+4)+5=[(x+1)(x+4)][(x+2)(x+3)]+5=(x2+5x
+4)(x2+5x+6)+5=(x2+5x+5-1)(x2+5x+5+1)+5=(x2+5x+5)2+4.设t=x2+5x+5,则y=t2+4.因为t=x2+5x+5=2-,x∈[-3,3],所以y=t2+4,t∈,抛物线开口向上,对称轴为直线t=0,所以ymin=4,故y=(x+1)(x+2)(x+3)(x+4)+5在区间[-3,3]上的最小值是4.
11. 已知二次函数f(x)=ax2+bx+c.
(1) 若f(-1)=0,试判断函数f(x)的零点个数;
(2) 若对x1,x2∈R,且x10,函数f(x)有两个零点.
(2) 令g(x)=f(x)-[f(x1)+f(x2)],则
g(x1)=f(x1)-[f(x1)+f(x2)]=,
g(x2)=f(x2)-[f(x1)+f(x2)]=,
所以g(x1)·g(x2)=-[f(x1)-f(x2)]2.
因为f(x1)≠f(x2),所以g(x1)·g(x2)<0,
所以g(x)=0在区间(x1,x2)上必有一个实数根,
即方程f(x)=[f(x1)+f(x2)]必有一个实数根属于(x1,x2).
12. 已知函数f(x)=ax2-1,a∈R,x∈R,集合A={x|f(x)=x},B={x|f(f(x))=x}且A=B≠,求实数a的取值范围.
解析:①若a=0,则A=B={-1};
②若a≠0,由A={x|ax2-x-1=0}≠,
得a≥-且a≠0.
集合B中元素为方程a(ax2-1)2-1=x,
即a3x4-2a2x2-x+a-1=0的实数根,
所以a3x4-2a2x2-x+a-1=(ax2-x-1)(a2x2+ax-a+1)=0.
因为A=B,
所以a2x2+ax-a+1=0无实数根或其根为ax2-x-1=0的根.
由a2x2+ax-a+1=0无实数根,得a<,
故a∈∪;
当a2x2+ax-a+1=0有实数根且为ax2-x-1=0的根时,
因为ax2-x-1=0,所以ax2=x+1,
所以a2x2+ax-a+1=a(x+1)+ax-a+1=0,
解得x=-,代入ax2-x-1=0得a=.
综上所述,实数a的取值范围是.
13. 已知二次函数f(x)=ax2+bx+1,若f(1)=0,且函数f(x)的值域为[0,+∞).
(1) 求a,b的值;
(2) 若h(x)=2f(x+1)+x|x-m|+2m,求h(x)的最小值.
解析:(1) 显然a≠0,因为f(1)=0,所以a+b+1=0.
又f(x)的值域为[0,+∞),所以Δ=b2-4a=0.
由解得
(2) 由(1)知f(x)=x2-2x+1,h(x)=2x2+x|x-m|+2m,
即h(x)=
①若m≥0,则h(x)min=min,
即h(x)min=min.
又2m2+2m-=≥0,所以当m≥0时,h(x)min=-+2m;
②若m<0,则h(x)min=h=2m-.
综上所述,h(x)min=