- 2021-06-16 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习求定积分的方法教案(全国通用)
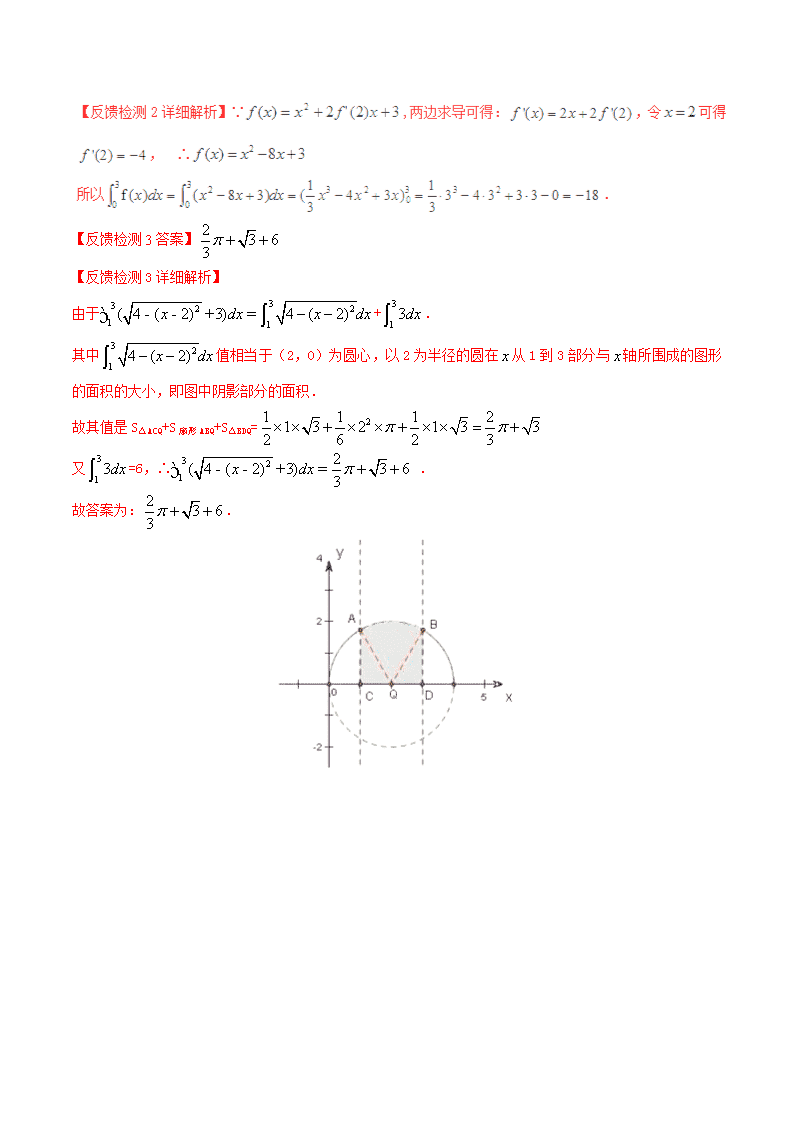
【例1】 定积分的值为____________. 【点评】本题要先利用定积分的性质化简,再利用微积分基本原理求解. 【反馈检测1】 . 【反馈检测2】若在上可导,,则 ( ) A. B. C. D. 方法二 数形结合利用面积求(几何法) 使用情景 不容易找到原函数. 解题步骤 先利用定积分的性质化简函数,再利用微积分基本原理求解. 【例2】计算的结果为( ). A.1 B. C. D. 【解析】先利用定积分的几何意义求:令,即 表示单位圆的(如图),即是圆面积,即;所以 =. 【点评】(1)本题中函数 的原函数不是很容易找到,所以先利用定积分的性质化简原式,再利用数形结合分析解答.(2)利用数形结合分析解答时,主要变量的范围,不要扩大了变量的范围,导致扩大了平面区域.,即表示单位圆的(如图),不是右半圆或整个圆.(3)等价转化是数里的重要数思想,它要求我们在每一步的变形和推理时,都必须注意等价变换. 【反馈检测3】 高中数常见题型解法归纳及反馈检测第18讲: 求定积分的方法参考答案 【反馈检测1答案】 【反馈检测1详细解析】 【反馈检测2答案】 【反馈检测3答案】 【反馈检测3详细解析】 由于+. 其中值相当于(2,0)为圆心,以2为半径的圆在从1到3部分与轴所围成的图形的面积的大小,即图中阴影部分的面积. 故其值是S△ACQ+S扇形ABQ+S△BDQ= 又=6,∴ . 故答案为:.查看更多