2020届二轮复习第9讲　立体几何的综合问题课件（23张）（江苏专用）

2020届二轮复习第9讲　立体几何的综合问题课件（23张）（江苏专用）

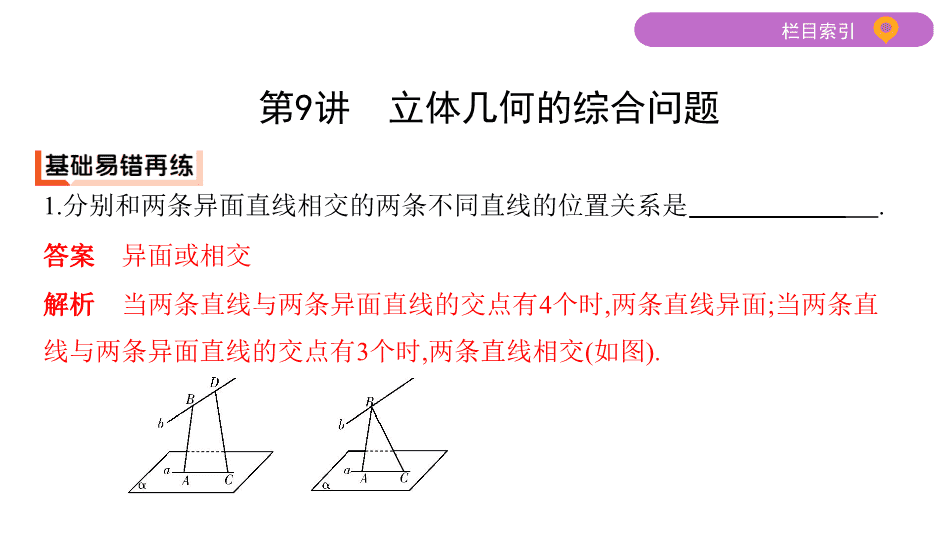
第 9 讲 立体几何的综合问题 第9讲　立体几何的综合问题 1.分别和两条异面直线相交的两条不同直线的位置关系是 　　　　　　      . 答案 　异面或相交 解析 　当两条直线与两条异面直线的交点有4个时,两条直线异面;当两条直 线与两条异面直线的交点有3个时,两条直线相交(如图). 2.过平面 α 外一条直线的平面 β 与平面 α 垂直,则平面 β 的个数可以是 　　　     　　　　     . 答案 　一个或无数个 解析 　若这条直线与平面 α 垂直,则平面 β 有无数个;若这条直线与平面 α 不垂 直,则平面 β 只有1个. 3.已知 α , β , γ 是三个平面, m , n 是两条直线,有下列四个命题:①如果 m ⊥ α , m ⊂ β , 那么 α ⊥ β ;②如果 m ⊥ n , m ⊥ α ,那么 n ∥ α ;③如果 α ⊥ β , m ∥ α ,那么 m ⊥ β ;④如果 α ∥ β , α ∩ γ = m , β ∩ γ = n ,那么 m ∥ n .其中正确的命题有 　　　     .(写出所有正确命 题的序号) 答案 　①④ 解析　 由面面垂直的判定定理可知①正确;如果 m ⊥ n , m ⊥ α ,那么 n , α 位置关 系不确定,可能平行或 n ⊂ α ,②错误;如果 α ⊥ β , m ∥ α ,那么 m , β 位置关系不确定, ③错误;由面面平行的性质定理可知④正确. 4.(2019如皋检测,8)如图所示的几何体是一个五面体,四边形 ABCD 为矩形, AB =4, BC =2,且 MN ∥ AB , MN =3,△ ADM 与△ BCN 都是正三角形,则此五面体的体 积为 　　　     . 答案        解析 　因为 AB =4, BC =2,且 MN ∥ AB , MN =3,△ ADM 与△ BCN 都是正三角形,所 以可将五面体补形为直三棱柱 ADE - BCF (如图),其中 NF ⊥ BF , BN =2, NF =   ,所 以 BF 2 = CF 2 =2 2 -   =   ,取 BC 的中点 O ,连接 FO ,则 FO =   =   ,所以 S △ BCF =   BC · FO =   ,故五面体的体积为 V ADE - BCF -2 V N - BCF =   × 4-2 ×   ×   ×   =   . 题型一　空间位置关系的证明与计算 例1     (2019苏锡常镇四市教学情况调查二,17)某工厂拟制造一个如图所示的 容积为36π立方米的有盖圆锥形容器. (1)若该容器的底面半径为6米,求该容器的表面积; (2)当容器的高为多少米时,制造该容器的侧面用料最省? 解析 　设圆锥形容器的底面半径为 r 米,高为 h 米,母线为 l 米,侧面积为 S 平方 米,容积为 V 立方米,则 V =36π. (1)由 r =6, V =   π r 2 h =36π,得 h =3, 所以 S =π rl =π r   =6π   =18   π, 又底面积为π r 2 =36π, 故该容器的表面积为(18   π+36π)=18(2+   )π(平方米). 答:该容器的表面积为18(2+   )π平方米. (2)由 V =   π r 2 h =36π,得 r 2 =   =   ,其中 h >0. 所以 S =π rl =π r   =π   =π   =π   =π     . 记 f ( h )=   + h ,则 f '( h )=-   +1=   ,令 f '( h )=0,得 h =6. 当 h ∈(0,6)时, f '( h )<0, f ( h )在(0,6)上单调递减; 当 h ∈(6,+ ∞ )时, f '( h )>0, f ( h )在(6,+ ∞ )上单调递增. 所以,当 h =6时, f ( h )最小,此时 S 最小. 答:当容器的高为6米时,制造该容器的侧面用料最省. 【方法归纳】　解决空间几何体体积计算问题的步骤大致有作、证、求,即 作出相关的辅助线,证明空间线面垂直,最后利用体积公式计算,所以要重视 逻辑推理在空间计算中的应用. 题型二　立体几何中的翻折问题 例2     (2018江苏高考信息预测)如图1,在平面多边形 BCDEF 中,四边形 ABCD 为正方形, EF ∥ AB , AB =2 EF =2,沿着 AB 将图形折成图2,其中∠ AED =90 ° , AE = ED , H 为 AD 的中点. (1)求证: EH ⊥ BD ; (2)求四棱锥 D - ABFE 的体积. 解析 　(1)证明:由题可知, AB ⊥ EA , AB ⊥ AD , 且 EA ∩ AD = A , EA , AD ⊂ 平面 AED . 所以 AB ⊥平面 AED . 因为 EH ⊂ 平面 AED ,所以 AB ⊥ EH . 因为 AE = ED , H 是 AD 的中点,所以 EH ⊥ AD . 又 AB ∩ AD = A , AB , AD ⊂ 平面 ABCD ,所以 EH ⊥平面 ABCD . 又因为 BD ⊂ 平面 ABCD ,所以 EH ⊥ BD . (2) V D - ABFE = V E - ABD + V B - DEF . 其中 V E - ABD =   ×   × AB × AD × EH =   × 2 × 2 × 1=   . 因为   =   ,且 V B - DFC = V F - BCD , 所以 V B - DEF =   V B - DFC =   V F - BCD , 所以 V D - ABFE = V E - ABD + V B - DEF =   +   ×   ×   × 2 × 2 × 1=1. 【方法归纳】　平面图形翻折问题的求解方法: ①解决与折叠有关问题的关键是搞清折叠前后的变量和不变量,一般情况下, 线段的长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的 突破口. ②在解决问题时,要综合考虑折叠前后的图形,既要分析折叠后的图形,也要 分析折叠前的图形. 2-1 　如图①所示,四边形 ABCD 中, AD ∥ BC , AD = AB ,∠ BCD =45 ° ,∠ BAD =90 ° , 将△ ABD 沿 BD 折起,记折起后 A 的位置为点 P ,且平面 PBD ⊥平面 BCD (如图 ②). 求证:(1) CD ⊥平面 PBD ;(2)平面 PBC ⊥平面 PDC . 证明　 (1)∵ AD = AB ,∠ BAD =90 ° , ∴∠ ABD =∠ ADB =45 ° . 又∵ AD ∥ BC ,∴∠ DBC =∠ ADB =45 ° . 又∠ DCB =45 ° ,∴∠ BDC =90 ° ,即 BD ⊥ DC . ∵平面 PBD ⊥平面 BCD ,平面 PBD ∩ 平面 BCD = BD , ∴ CD ⊥平面 PBD . (2)由 CD ⊥平面 PBD 得 CD ⊥ BP . 又 BP ⊥ PD , PD ∩ CD = D ,∴ BP ⊥平面 PDC , 又 BP ⊂ 平面 PBC ,∴平面 PBC ⊥平面 PDC . 题型三　立体几何中的探索性问题 例3     (2019苏州中学期初,16)如图,棱柱 ABCD - A 1 B 1 C 1 D 1 的底面 ABCD 为菱形, 平面 AA 1 C 1 C ⊥平面 ABCD . (1)证明: BD ⊥平面 AA 1 C 1 C ; (2)在直线 CC 1 上是否存在点 P ,使 BP ∥平面 DA 1 C 1 ?若存在,求出点 P 的位置;若 不存在,说明理由. 解析 　(1)证明:因为四边形 ABCD 为菱形 ⇒ BD ⊥ AC ,平面 AA 1 C 1 C ⊥平面 ABCD ,平面 AA 1 C 1 C ∩ 平面 ABCD = AC ,所以 BD ⊥平面 AA 1 C 1 C . (2)存在,点 P 在 C 1 C 的延长线上,且 C 为 C 1 P 的中点. 连接 B 1 C . 因为 A 1 B 1 ∥ AB ∥ DC , 所以四边形 A 1 B 1 CD 为平行四边形, 所以 A 1 D ∥ B 1 C . 在 C 1 C 的延长线上取点 P ,使 C 1 C = CP ,连接 BP , 因为 B 1 B ∥ CC 1 , BB 1 = CC 1 , 所以 BB 1 ∥ CP , BB 1 = CP , 所以四边形 BB 1 CP 为平行四边形,所以 BP ∥ B 1 C , 所以 BP ∥ A 1 D . 因为 BP ⊄ 平面 A 1 DC 1 , A 1 D ⊂ 平面 A 1 DC 1 , 所以 BP ∥平面 DA 1 C 1 . 【方法归纳】　立体几何中的探索性问题主要是对平行、垂直关系的探究 以及对条件和结论不完备的开放性问题的探究,解决这类问题一般根据探索 性问题的设问,假设其存在并探索出结论,然后在这个假设下进行推理论证, 若得到合乎情理的结论,则肯定假设,若得到矛盾的结论,则否定假设. 3-1 　如图,在四棱锥 P - ABCD 中, PA ⊥平面 ABCD ,底面 ABCD 为菱形, E 为 CD 的 中点. (1)求证: BD ⊥平面 PAC ; (2)若∠ ABC =60 ° ,求证:平面 PAB ⊥平面 PAE ; (3)棱 PB 上是否存在点 F ,使得 CF ∥平面 PAE ?说明理由. 解析 　本题考查了直线与平面平行、垂直的判定和性质,通过线线、线面、 面面平行、垂直的相互转化考查了学生的空间想象能力和转化的思想方法, 体现了直观想象、逻辑推理的核心素养. (1)证明:因为 PA ⊥平面 ABCD , BD ⊂ 平面 ABCD , 所以 PA ⊥ BD . 又因为底面 ABCD 为菱形,所以 BD ⊥ AC .又因为 PA ∩ AC = A , 所以 BD ⊥平面 PAC . (2)证明:因为 PA ⊥平面 ABCD , AE ⊂ 平面 ABCD , 所以 PA ⊥ AE . 因为底面 ABCD 为菱形,∠ ABC =60 ° ,所以∠ ADC =60 ° ,所以△ ADC 为等边三角 形.因为 E 为 CD 的中点, 所以 AE ⊥ CD .因为 AB ∥ CD ,所以 AB ⊥ AE . 又因为 PA ∩ AB = A ,所以 AE ⊥平面 PAB . 又因为 AE ⊂ 平面 PAE ,所以平面 PAB ⊥平面 PAE . (3)棱 PB 上存在点 F ,使得 CF ∥平面 PAE .理由如下: 取 PB 的中点 F ,取 PA 的中点 G ,连接 CF , FG , EG . 则 FG ∥ AB ,且 FG =   AB . 因为底面 ABCD 为菱形,且 E 为 CD 的中点, 所以 CE ∥ AB ,且 CE =   AB . 所以 FG ∥ CE ,且 FG = CE . 所以四边形 CEGF 为平行四边形.所以 CF ∥ EG . 因为 CF ⊄ 平面 PAE , EG ⊂ 平面 PAE , 所以 CF ∥平面 PAE .