河北省衡水市武邑县武邑中学2019-2020学年高一上学期期中考试数学试题

河北省衡水市武邑县武邑中学2019-2020学年高一上学期期中考试数学试题

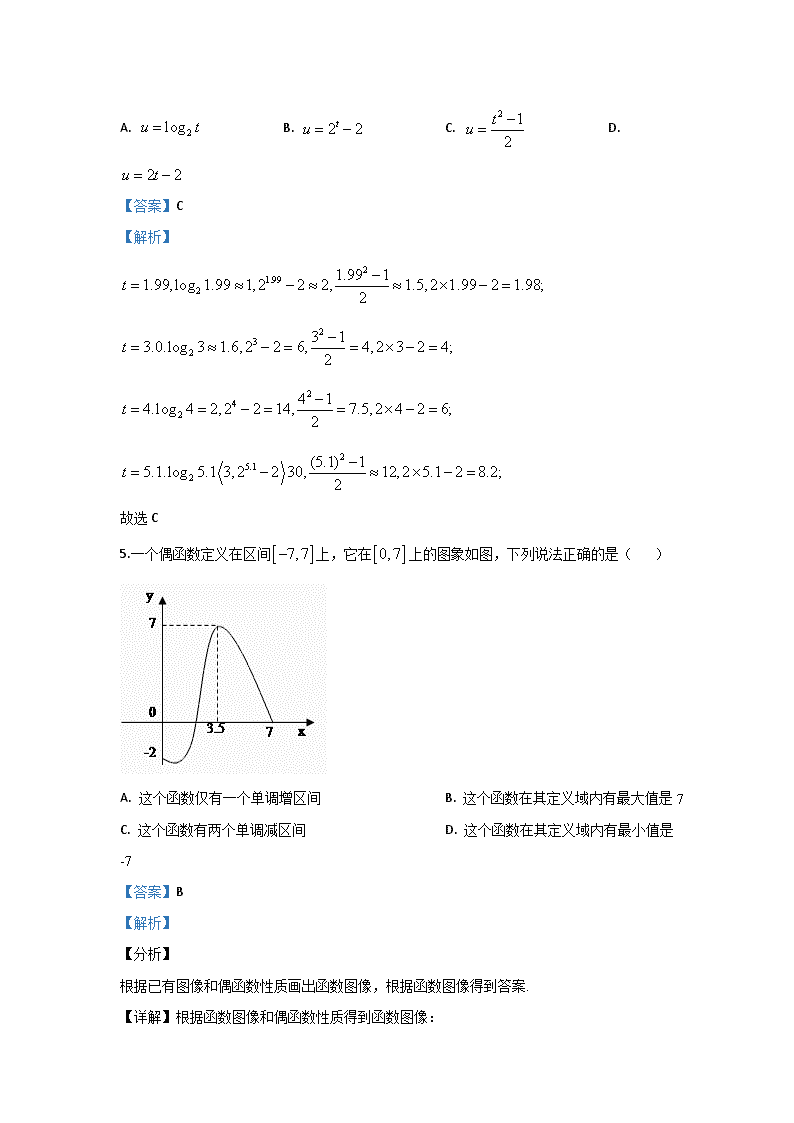
河北武邑中学2019-2020学年高一上学期期中考试 数学试题 注意事项：‎ ‎1.本试卷分第Ⅰ卷（选择题）和Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟.‎ ‎2.答题前请仔细阅读答题卡（纸）上的“注意事项”，按照“注意事项”的规定答题.‎ ‎3.选择题答案涂在答题卡上，非选择题答案写在答题卡上相应位置，在试卷和草稿纸上作答无效.‎ 第Ⅰ卷选择题（共60分）‎ 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求，将正确答案填涂在答题卡上.‎ ‎1.设全集，集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 由题意得：,，‎ ‎∴=，‎ ‎∴() A=‎ 故选：D 点睛：1.用描述法表示集合，首先要弄清集合中代表元素的含义，再看元素的限制条件，明确集合类型，是数集、点集还是其他的集合．‎ ‎2．求集合的交、并、补时，一般先化简集合，再由交、并、补的定义求解．‎ ‎3．在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化．一般地，集合元素离散时用Venn图表示；集合元素连续时用数轴表示，用数轴表示时要注意端点值的取舍．‎ ‎2.已知，则( )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由指数幂运算即可求解 ‎【详解】，则.‎ 故选D.‎ ‎【点睛】本题考查指数幂运算，熟记运算性质是关键，注意运算的准确，是基础题 ‎3.在映射中，，且，则中的元素在集合中的象为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 试题分析：由题意，对应关系为，故中的元素在集合中的象为 考点：映射，象与原象 ‎4.今有一组实验数据如下表所示：‎ t ‎ ‎1.99 ‎ ‎3.0 ‎ ‎4.0 ‎ ‎5.1 ‎ ‎6.12 ‎ u ‎ ‎1.5 ‎ ‎4.04 ‎ ‎7.5 ‎ ‎12 ‎ ‎18.01 ‎ 则最佳体现这些数据关系的函数模型是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 故选C ‎5.一个偶函数定义在区间上，它在上的图象如图，下列说法正确的是（ ）‎ A. 这个函数仅有一个单调增区间 B. 这个函数在其定义域内有最大值是7‎ C. 这个函数有两个单调减区间 D. 这个函数在其定义域内有最小值是-7‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据已有图像和偶函数性质画出函数图像，根据函数图像得到答案.‎ ‎【详解】根据函数图像和偶函数性质得到函数图像：‎ 由图像可知：‎ 这个函数有三个单调增区间；‎ 这个函数有三个单调减区间；‎ 这个函数在其定义域内有最大值是 ；‎ 这个函数在其定义域内最小值不是．‎ 故选：‎ ‎【点睛】本题考查了函数的图像，单调性，最值，意在考查学生对于函数图像的应用.‎ ‎6.已知，则使函数的值域为，且为奇函数的所有的值为( 　)‎ A. 1，3 B. －1，‎1 ‎C. －1，3 D. －1，1，3‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据幂函数的性质，分别判断幂函数的值域和奇偶性是否满足条件即可．‎ ‎【详解】当a=﹣1时，y=，为奇函数，但值域为{x|x≠0}，不满足条件．‎ 当a=1时，y=x，为奇函数，值域为R，满足条件．‎ 当a=2时，y=x2为偶函数，值域为{x|x≥0}，不满足条件．‎ 当a=3时，y=x3为奇函数，值域为R，满足条件．‎ 故选：A．‎ ‎【点睛】本题主要考查幂函数的图象和性质，比较基础．‎ ‎7.已知，，，则，，的大小关系为（）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据的单调性判断的大小关系，由判断出三者的大小关系.‎ ‎【详解】由，，，则.故选C.‎ ‎【点睛】本小题主要考查对数运算，考查对数函数的单调性，考查对数式比较大小，属于基础题.‎ ‎8.已知函数在上单调递减，且是偶函数，则，，的大小关系是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 先根据条件得到的图象关于直线对称，且在上单调递增，然后通过比较到对称轴距离的大小可得所求结果．‎ ‎【详解】由是偶函数可得其图象的对称轴为，‎ 所以函数的图象关于直线对称．‎ 又函数在上单调递减，‎ 所以函数在上单调递增．‎ 因为，‎ 所以，即．‎ 故选D．‎ ‎【点睛】比较函数值大小的常用方法：（1）将自变量转化到同一单调区间上，然后根据函数的单调性进行比较；（2）对于图象有对称轴的函数来讲，可将函数值的大小问题转化为自变量到对称轴的距离的大小的问题求解．‎ ‎9.当时，函数满足，则函数的图像大致为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ 试题分析：由函数（且）满足，故的图象应是C图，故选C．‎ 考点：函数的图象．‎ ‎10.已知函数=满足则的解集是 A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ 因为函数满足,所以 <,则函数是减函数,所以可化为,求解可得或 ,故选C.‎ ‎11.设x，y为实数，且满足，则（ ）‎ A. 2 B. ‎5 ‎C. 10 D. 2018‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由题意可设，由导数判断单调性，由奇偶性的定义判断为奇函数，可得，由单调性可得x，y的和．‎ ‎【详解】由题意可设，‎ 可得导数，‎ 即为R上的增函数；‎ 又，‎ 即为奇函数，‎ ‎，可得 ‎，‎ 可得，‎ 由在R上递增，可得，‎ 即有．‎ 故选：A．‎ ‎【点睛】本题考查函数方程的转化思想，构造函数判断奇偶性和单调性是解题的关键，属于中档题．‎ ‎12.高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设，用表示不超过的最大整数，则称为高斯函数，例如：，，已知函数，则函数的值域是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎，奇函数，函数化简得出：，，‎ ‎，当时，，当时，，当时，，函数的值域为，故选D.‎ ‎【方法点睛】本题考查函数的值域、指数式的运算以及新定义问题，属于难题. 新定义题型的特点是：通过给出一个新概念，或约定一种新运算，或给出几个新模型来创设全新的问题情景，要求考生在阅读理解的基础上，依据题目提供的信息，联系所学的知识和方法，实现信息的迁移，达到灵活解题的目的.遇到新定义问题，应耐心读题，分析新定义的特点，弄清新定义的性质，按新定义的要求，“照章办事”，逐条分析、验证、运算，使问题得以解决.本题定义高斯函数达到考查函数的值域、指数式的运算的目的.‎ 第Ⅱ卷非选择题（共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分，将答案填在答题卡上相应位置.‎ ‎13.已知，则______.‎ ‎【答案】2‎ ‎【解析】‎ ‎【分析】‎ 直接取代入计算得到答案.‎ ‎【详解】取得到 故答案为：‎ ‎【点睛】本题考查了函数值的计算，也可以先计算出函数解析式再求值.‎ ‎14.已知函数在区间上的最大值为_____________．‎ ‎【答案】-4‎ ‎【解析】‎ 试题分析：由题意，得在上为减函数，则在也为减函数；所以当时，‎ ‎.‎ 考点：函数的单调性与最值.‎ ‎15.若函数定义域为，则实数取值范围是______.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 题目等价于恒成立，讨论和两种情况，计算得到答案.‎ ‎【详解】函数的定义域为，即恒成立.‎ 当时，易知成立.‎ 当时，需满足： ‎ 综上所述： ‎ 故答案为：‎ ‎【点睛】本题考查了函数的定义域，忽略掉的情况是容易发生的错误.‎ ‎16.．如果对于函数定义域内任意的两个自变量的值，当时,都有，且存在两个不相等的自变量值,使得,就称为定义域上的不严格的增函数．已知函数的定义域、值域分别为、，,, 且为定义域上的不严格的增函数，那么这样的共有____个．‎ ‎【答案】9‎ ‎【解析】‎ ‎【分析】‎ 由题意结合新定义的知识分类讨论满足题意的函数的个数即可.‎ ‎【详解】由不严格的增函数的定义可知函数的值域为一个数或两个数，‎ 当值域为一个数时：‎ ‎，，共三种情况，‎ 当值域为两个数时：‎ ‎，，，‎ ‎，，，‎ 综上可得，函数共有9个.‎ ‎【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.对于此题中的新概念，对阅读理解能力有一定的要求.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝.‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.‎ ‎17.已知集合，或．‎ ‎（1）若，求；‎ ‎（2）若，求实数的取值范围．‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）把等于带入集合中求交集即可。‎ ‎（2）由，可知包含数轴上所有实数，画出数轴分析即可。‎ ‎【详解】（1）当时，，，‎ 所以；‎ ‎（2）因为，所以，‎ 解得：.‎ ‎【点睛】本题主要考查了集合之间的运算，需要掌握集合的交集、并集、补集之间的运算，属于基础题。‎ ‎18.有一种候鸟每年都按一定的路线迁徙，飞往繁殖地产卵，科学家经过测量发现候鸟的飞行速度可以表示为函数，单位是，其中表示候鸟每分钟耗氧量的单位数，为表示测量过程中候鸟每分钟的耗氧偏差.（参考数据：，，）‎ ‎（1）若，候鸟停下休息时，它每分钟的耗氧量为多少个单位？‎ ‎（2）若雄鸟的飞行速度为，雌鸟的飞行速度为，那么此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的多少倍？‎ ‎【答案】（1）候鸟停下休息时，它每分钟的耗氧量为466个单位（2）此时雄鸟每分钟的耗氧量是雌鸟每分钟的耗氧量的9倍.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）将，代入函数，计算得到答案.‎ ‎（2）根据题意得到方程组，两式相减化简得到答案.‎ ‎【详解】（1）将，代入函数式可得，‎ 即.所以，于是.‎ 故候鸟停下休息时，它每分钟的耗氧量为466个单位.‎ ‎（2）设雄鸟每分钟的耗氧量为，雌鸟每分钟的耗氧量为，依题意可得 ‎，‎ 两式相减可得，于是，‎ 故此时雄鸟每分钟的耗氧量是雌鸟每分钟的耗氧量的9倍.‎ ‎【点睛】本题考查了函数的应用，意在考查学生的计算能力和应用能力.‎ ‎19.已知函数，且，的定义域为.‎ ‎（1）求的值及函数的解析式；‎ ‎（2）若方程有解，求实数的取值范围.‎ ‎【答案】（1），（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据代入函数计算得到，继而得到函数解析式.‎ ‎（2），函数变换为得到计算得到答案.‎ ‎【详解】（1），所以，所以.‎ ‎（2），令，‎ 所以，在上单调递减，‎ 所以，即.‎ ‎【点睛】‎ 本题考查了函数的解析式，方程的解的问题，将方程解的问题转化为函数的值域是解题的关键.‎ ‎20.已知奇函数的定义域为，其中为指数函数且的反函数过点.‎ ‎（1）求函数的解析式；‎ ‎（2）判断函数的单调性，并用函数单调性定义证明.‎ ‎【答案】（1）（2）在上单调递减，证明见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）先计算，再根据解得，得到解析式.‎ ‎（2）先判断函数单调递减，设，计算，利用定义法得到证明.‎ ‎【详解】（1）设，由的图象过点，可得，∴，‎ 故函数.‎ 再根据为奇函数，可得，∴，‎ 即.检验：，∴是奇函数.‎ ‎∴.‎ ‎（2），∴在上单调递减.‎ 证明：设，则，由于，，可得，‎ ‎∴，即 故在上单调递减.‎ ‎【点睛】本题考查了函数的解析式，函数的单调性，意在考查学生对于函数性质的灵活运用.‎ ‎21.已知函数.‎ ‎（1）当时，求值域；‎ ‎（2）若存在单调递增区间，求的取值范围.‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1），计算定义域为，得到，代入得到值域.‎ ‎（2）讨论和两种情况，计算得到答案.‎ ‎【详解】（1）当时，，‎ 设，‎ 由，得，得，即函数的定义域为，‎ 此时，‎ 则，即函数的值域为.‎ ‎（2）若存在单调递增区间，‎ 则当，则函数存在单调递增区间即可，‎ 则判别式得或（舍）， ‎ 当，则函数存在单调递减区间即可，则判别式得或，此时不成立，‎ 综上所述：实数的取值范围是.‎ ‎【点睛】本题考查了函数的值域和单调性，忽略掉定义域是容易发生的错误.‎ ‎22.已知函数.‎ ‎（1）若，求函数的单调递增区间；‎ ‎（2）当时，若对任意的，不等式恒成立，求实数的取值范围.‎ ‎【答案】（1）函数的单调递增区间为，（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）化简得到，画出函数图像得到单数单调区间.‎ ‎（2）化简得到，讨论，和 三种情况，计算得到答案.‎ ‎【详解】（1）当时，.‎ 画出函数图像：‎ 由函数的图像可知，函数的单调递增区间为，.‎ ‎（2）不等式化，‎ 即：，对任意的恒成立.‎ 因为，所以分如下情况讨论：‎ ‎①时，不等式化为恒成立.‎ 即对恒成立.‎ ‎∵在上单调递增，‎ 只需，∴.‎ ‎②当时，不等式化为恒成立，‎ 即对恒成立，‎ 由①知，∴在上单调递减，‎ ‎∴只需，∴或，‎ ‎∵，∴.‎ ‎③当时，不等式化为恒成立，‎ 即对恒成立，‎ 在上单调递增，‎ ‎∴只需，∴或，‎ 由②得：，‎ 综上所述，的取值范围是：.‎ ‎【点睛】本题考查了函数的单调性，不等式恒成立问题，将恒成立问题转化为函数的最值问题是解题的关键.‎