- 2021-06-16 发布 |
- 37.5 KB |
- 41页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习专题4第1讲等差数列、等比数列课件(42张)(全国通用)
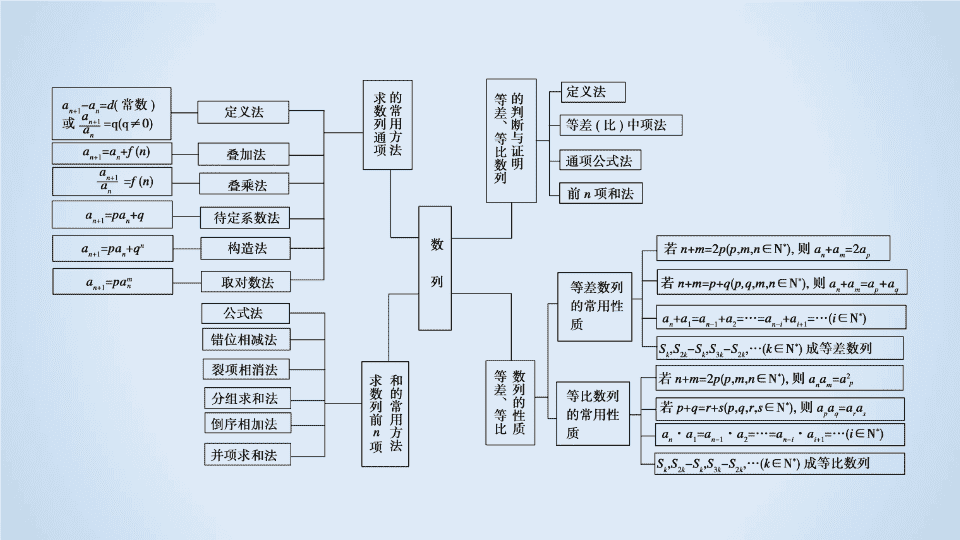
第一部分 专题强化突破 专题四 数 列 知识网络构建 第一讲 等差数列、等比数列 1 高考考点聚焦 2 核心知识整合 3 高考真题体验 4 命题热点突破 5 课后强化训练 高考考点聚焦 高考考点 考点解读 等差 ( 比 ) 数列的基本运算 1. 在等差 ( 比 ) 数列中, a 1 , a n , S n , n , d ( q ) 这五个量中已知其中的三个量,求另外两个量 2 .考查等差 ( 比 ) 数列的通项公式,前 n 项和公式,考查方程的思想以及运算能力 等差 ( 比 ) 数列的判断与证明 1. 以递推数列为载体,考查等差 ( 比 ) 数列的定义或等差 ( 比 ) 中项 2 .以递堆数列为命题背景考查等差 ( 比 ) 数列的证明方法 等差 ( 比 ) 数列的性质 1. 等差 ( 比 ) 数列项或和的一些简单性质的应用 2 .常与数列的项或前 n 项和结合考查等差 ( 比 ) 数列的性质 备考策略 本部分内容在备考时应注意以下几个方面: (1) 加强对等差 ( 比 ) 数列概念的理解,掌握等差 ( 比 ) 数列的判定与证明方法. (2) 掌握等差 ( 比 ) 数列的通项公式、前 n 项和公式,并会应用. (3) 掌握等差 ( 比 ) 数列的简单性质并会应用. 预测 2018 年命题热点为: (1) 在解答题中,涉及等差、等比数列有关量的计算、求解. (2) 已知数列满足的关系式,判定或证明该数列为等差 ( 比 ) 数列. (3) 给出等差 ( 比 ) 数列某些项或项与项之间的关系或某些项的和,求某一项或某些项的和. 核心知识整合 1 . 重要公式 (1) 等差数列通项公式: a n = ________________________ . (2) 等差数列前 n 项和公式: S n = __________ = __________________ . (3) 等比数列通项公式: _____________ . a 1 + ( n - 1) d a n = a 1 q n - 1 (4) 等比数列前 n 项和公式: S n = _________________________ . (5) 等差中项公式: ____________________________________ . (6) 等比中项公式: ________________________________ . (7) 数列 { a n } 的前 n 项和 S n 与通项 a n 之间的关系: a n = ___________________ . 2 a n = a n - 1 + a n + 1 ( n ∈ N * , n ≥ 2) a = a n - 1 · a n + 1 ( n ∈ N * , n ≥ 2) 2 . 重要结论 (1) 通项公式的推广:等差数列中, a n = _________________ ; 等比数列中, a n = __________ . (2) 增减性: ① 等差数列中,若公差大于零,则数列为 __________ ;若公差小于零,则数列为 __________ . ② 等比数列中,若 a 1 >0 且 q >1 或 a 1 <0 且 0< q <1 ,则数列为 ___________ ;若 a 1 >0 且 0< q <1 或 a 1 <0 且 q >1 ,则数列为 ___________ . (3) 等差数列 { a n } 中, S n 为前 n 项和. __________________________ 仍成等差数列;等比数列 { b n } 中, T n 为前 n 项和. T n , T 2 n - T n , T 3 n - T 2 n , … 一般仍成等比数列. a m + ( n - m ) d a m · q n - m 递增数列 递减数列 递增数列 递减数列 S n , S 2 n - S n , S 3 n - S 2 n , … 1 . 忽视等比数列的条件: 判断一个数列是等比数列时,忽视各项都不为零的条件. 2 . 漏掉等比中项: 正数 a , b 的等比中项是 ± ,容易漏掉-. 3 . 忽略对等比数列的公比的讨论: 应用等比数列前 n 项和公式时应首先讨论公式 q 是否等于 1 . 高考真题体验 C A C [ 解析 ] 设等差数列 { a n } 的公差为 d ,因为 { a n } 为等差数列,且 S 9 = 9 a 5 = 27 ,所以 a 5 = 3. 又 a 10 = 8 ,解得 5 d = a 10 - a 5 = 5 ,所以 d = 1 ,所以 a 100 = a 5 + 95 d = 98 ,选 C . 1 32 命题热点突破 命题方向 1 等差、等比数列的基本运算 B D 『 规律总结 』 在等差 ( 比 ) 数列问题中最基本的量是首项 a 1 和公差 d ( 公比 q ) ,在解题时往往根据已知条件建立关于这两个量的方程组,从而求出这两个量,那么其他问题也就会迎刃而解,这就是解决等差、等比数列问题的基本量的方法,这其中蕴含着方程思想的运用. 提醒:应用等比数列前 n 项和公式时,务必注意公比 q 的取值范围 . 6 命题方向 2 等差、等比数列的基本性质 D C A C 命题方向 3 等差、等比数列的判断与证明 『 规律总结 』 判断或证明数列是否为等差或等比数列,一般是依据等差数列、等比数列的定义,或利用等差中项、等比中项进行判断. 提醒:利用 a = a n + 1 · a n - 1 ( n ≥ 2) 来证明数列 { a n } 为等比数列时,要注意数列中的各项均不为 0 . 课后强化训练查看更多