- 2021-06-16 发布 |
- 37.5 KB |
- 3页


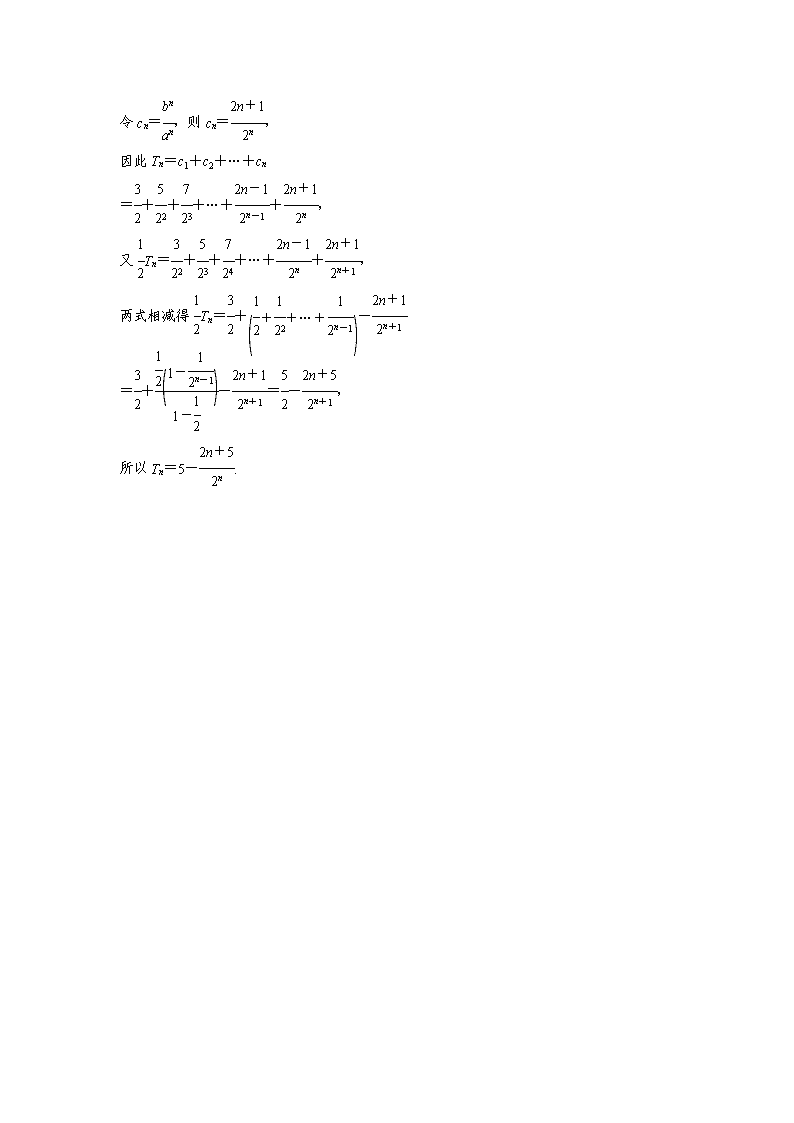
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习(文) 数列的通项与求和问题学案(全国通用)
规范答题示例5 数列的通项与求和问题 典例5 (12分)下表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N*).已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.且a11=1,a31+a61=9,a35=48. a11 a12 a13 … a1n a21 a22 a23 … a2n a31 a32 a33 … a3n … … … … … an1 an2 an3 … ann (1)求an1和a4n; (2)设bn=+(-1)n·an1(n∈N*),求数列{bn}的前n项和Sn. 审题路线图 ―→ 规 范 解 答·分 步 得 分 构 建 答 题 模 板 解 (1)设第1列依次组成的等差数列的公差为d,设每一行依次组成的等比数列的公比为q.依题意a31+a61=(1+2d)+(1+5d)=9,∴d=1, ∴an1=a11+(n-1)d=1+(n-1)×1=n, 3分 ∵a31=a11+2d=3,∴a35=a31·q4=3q4=48, ∵q>0,∴q=2,又∵a41=4, ∴a4n=a41qn-1=4×2n-1=2n+1. 6分 (2)∵bn=+(-1)nan1=+(-1)n·n 7分 =+(-1)n·n=-+(-1)n·n, ∴Sn=+++…+ 第一步 找关系:根据已知条件确定数列的项之间的关系. 第二步 求通项:根据等差或等比数列的通项公式或利用累加、累乘法求数列的通项公式. 第三步 定方法:根据数列表达式的结构特征确定求和方法(常用的有公式法、裂项相消法、错位相减法、分组法等). 第四步 写步骤. 第五步 再反思:检查求和过程中各项的符号有无错误,用特殊项估算结果. +[-1+2-3+4-5+…+(-1)nn],10分 当n为偶数时,Sn=1-+, 11分 当n为奇数时, Sn=1-+-n=1--=-. 12分 评分细则 (1)求出d给1分,求an1时写出公式结果错误给1分;求q时没写q>0扣1分; (2)bn写出正确结果给1分,正确进行裂项再给1分; (3)缺少对bn的变形直接计算Sn,只要结论正确不扣分; (4)当n为奇数时,求Sn中间过程缺一步不扣分. 跟踪演练5 (2017·山东)已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3. (1)求数列{an}的通项公式; (2){bn}为各项非零的等差数列,其前n项和为Sn,已知S2n+1=bnbn+1,求数列的前n项和Tn. 解 (1)设{an}的公比为q, 由题意知a1(1+q)=6,aq=a1q2, 又an>0,由以上两式联立方程组解得a1=2,q=2, 所以an=2n. (2)由题意知S2n+1= =(2n+1)bn+1, 又S2n+1=bnbn+1,bn+1≠0, 所以bn=2n+1. 令cn=,则cn=, 因此Tn=c1+c2+…+cn =+++…++, 又Tn=+++…++, 两式相减得Tn=+- =+-=-, 所以Tn=5-.查看更多