- 2021-06-16 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习算法与程序框图教案(全国通用)
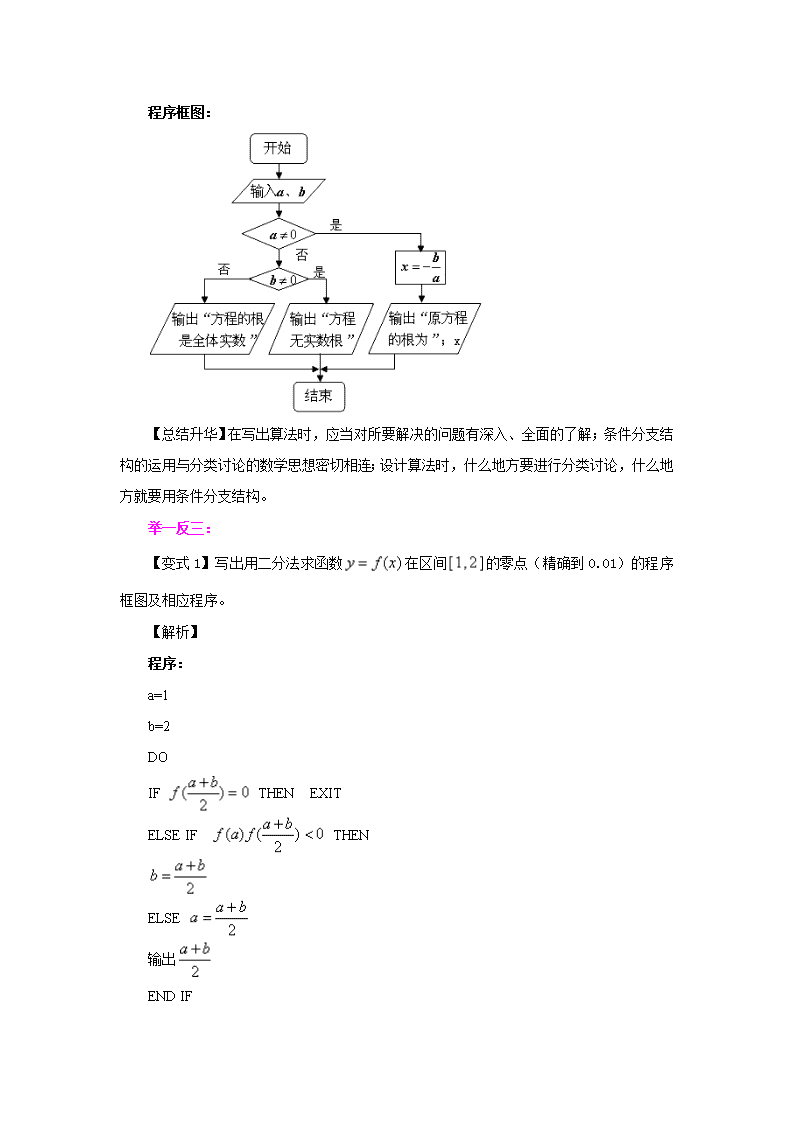
2020届二轮复习 算法与程序框图 教案(全国通用) 类型一:算法的含义 【例1】已知球的表面积是16π,要求球的体积,写出解决该问题的一个算法. 【思路点拨】先根据表面积算出球的半径,再根据球的体积公式求出球的体积,将上面步骤分解并分别写出即可得到算法。 【解析】算法如下: 第一步,s=16π. 第二步,计算 第三步,计算 第四步,输出V. 【总结升华】给出一个问题,设计算法应该注意: (1)认真分析问题,联系解决此问题的一般数学方法,此问题涉及到的各种情况; (2)将此问题分成若干个步骤; (3)用简练的语句将各步表述出来. 举一反三: S=1 I=3 While I< ① S=S×I I=I+2 End While Print S End 【变式1】设计一个计算1×3×5×7×9×11×13的算法.图中给出程序的一部分,则在横线①上不能填入的数是( ) A.13 B.13.5 C.14 D.14.5 【解析】当I<13成立时,只能运算 1×3×5×7×9×11.故选A. 【变式2】写出找出1至1 000内7的倍数的一个算法. 解答:算法1: S1 令A=0; S2 将A不断增加1,每加一次,就将A除以7,若余数为0,则找 到了一个7的倍数,将其输出; S3 反复执行第二步,直到A=1 000结束. 算法2: S1 令k=1; S2 输出k·7的值; S3 将k的值增加1,若k·7的值小于1 000,则返回S2,否则结束. 算法3: S1 令x=7; S2 输出x的值; S3 将x的值增加7,若没有超过1 000,则返回S2,否则结束. 类型二:程序框图 【例2】写出解方程()的相应程序及程序框图。 【思路点拨】因为,解方程时需要先对最高次项的系数是否为0进行判断。 若,则方程的解为; 若,则需要再次判断是否为0, 若,则方程的解为全体实数, 若,则方程无实数解。 据此可以用条件语句来实现。 【解析】程序: INPUT“a,b=”;a,b IF a<>=0 THEN PRINT“原方程的根为”; ELSE IF b<>=0 THEN PRINT“方程无实数根” ELSE PRINT“方程的根为全体实数” END IF END IF END 程序框图: 【总结升华】在写出算法时,应当对所要解决的问题有深入、全面的了解;条件分支结构的运用与分类讨论的数学思想密切相连;设计算法时,什么地方要进行分类讨论,什么地方就要用条件分支结构。 举一反三: 【变式1】写出用二分法求函数在区间的零点(精确到0.01)的程序框图及相应程序。 【解析】 程序: a=1 b=2 DO IF THEN EXIT ELSE IF THEN ELSE 输出 END IF LOOP UNTIL PRINT 程序框图: 开始 结束 【例3高清视频算法与程序框图例题2】执行如图所示的框图,输入N=5,则输出的数等于( ) 【思路点拨】 根据程序框图(算法流程图)分析出该程序框图的功能进行求解. 【总结升华】 识别运行算法框图和完善算法框图是高考的热点. 解答这一类问题, 第一,要明确算法框图的顺序结构、选择结构和循环结构; 第二,要识别运行算法框图,理解框图所解决的实际问题; 第三,按照题目的要求完成解答.对算法框图的考查常与数列和 函数等知识相结合,进一步强化框图问题的实际背景. 类型三:条件结构 【例3】已知函数,写出求该函数的函数值的算法并画出程序框图。 【思路解析】分析算法写出算法选择合适的逻辑结构画出程序框图。 【解析】算法如下: 第一步:输入; 第二步:如果,那么使, 否则; 第三步:输出。 程序框图如下: 【总结升华】求分段函数值的算法应用到条件结构,因此在程序框图的画法中需要引入判断框,要根据题目的要求引入判断框的个数,而判断框内的条件不同,对应的框图中的内容或操作就相应地进行变化. 举一反三: 【变式1】阅读如图的程序框图,若输出s 的值为-7,则判断框内可填写( ) A.i<3? B.i<4? C.i<5? D.i<6? 【解析】i=1,s=2-1=1; i=3,s=1-3=-2; i=5,s=-2-5=-7.所以选D. 【变式2】写出解方程的一个算法,并画出程序框图。 【解析】 算法步骤: 第一步:判断是否等于0 如果,则解得; 如果,则执行第二步; 第二步:计算; 第三步:若,则原方程无实数根;否则,,有,; 第四步:输出方程无实数根的信息或、。 程序框图: 开始 结束 是 否 是 否 类型四:循环结构 【例4】设计算法求的值,并画出程序框图。 【思路点拨】(1)这是一个累加求和问题,共99项相加; (2)设计一个计数变量,一个累加变量,用循环结构实现这一算法。 【解析】算法如下: 第一步:令S=0, 第二步:若成立,则执行第三步; 否则,输出S,结束算法; 第三步: 第四步:,返回第二步。 程序框图: 方法一:当型循环程序框图: 方法二:直到型循环程序框图: 【总结升华】利用循环结构表示算法,一定要先确定是利用当型循环结构,还是直到型循环结构;第二要选择准确的表示累计的变量;第三要注意在哪一步开始循环。 举一反三: 【变式】设计一个计算10个数的平均数的算法,并画出程序框图. 【解析】算法步骤如下: 第一步,令S=0. 第二步,令I=1. 第三步,输入一个数G. 第四步,令S=S+G. 第五步,令I=I+1. 第六步,若I>10,转到第七步, 若I≤10,转到第三步. 第七步,令A=S/10. 第八步,输出A. 据上述算法步骤,程序框图如图. 类型五:输入、输出、赋值语句的应用 【例5】阅读程序框图(如下图),若输入m=4,n=6,则输出a= ,i= . 【解析】a=12,i=3. 【点拨】赋值语句是一种重要的基本语句,也是程序必不可少的重要组成部分,使用赋值语句,要注意其格式要求. 【例6】阅读下列程序,并回答问题. (1)程序 (2)程序 INPUT A,B,C A=A+B B=B-A C=C/A*B PRINT “C=”;C END INPUT a,b c=a―b b=a+c―b PRINT a,b,c END (1)中若输入1,2,则输出的结果为________; (2)中若输入3,2,5,则输出的结果为________. 【答案】(1)1,―2,―1(2)C=―3 【解析】 分别将输入的值代入程序中逐步计算即可,要注意赋值前后变量值的变化. (1)阅读程序,由a=1,b=2,c=a―b可得c=―1;又根据语句b=a+c―b,可得b=―2; 所以程序运行后的结果为:1,―2,―1. (2)阅读程序,由A=3,B=2,C=5,A=A+B,可得A=5, 又根据语句B=B―A,可得B=―3, 又C=C/A*B,所以输出结果为C=―3. 【点评】赋值语句在给变量赋值时,先计算赋值号右边的式子然后赋值给赋值号左边的变量;另外可以给一个变量先后多次赋不同的值,但变量的取值只与最后一次赋值有关.解决此类问题时要时刻把握某个变量在该程序中充当的角色,时刻关注其值的改变情况. 举一反三: 【变式】写出下列语句描述的算法的输出结果. a=5 b=3 c=(a+b)/2 d=c*c PRINT “d=”;d END (1) a=1 b=2 c=a+b b=a+c―b PRINT “a=,b=,c=”;a,b,c END (2) a=10 b=20 c=30 a=b b=c c=a PRINT “a=,b=,c=”;a,b,c END (3) 【答案】(1)16 (2)a=1 b=2 c=3(3)a=20 b=30 c=20 【解析】 (1)∵a=5,b=3,,∴d=c2=16. (2)∵a=1,b=2,c=a+b,∴c=3.又将a+c―b赋值给b,∴b=1+3-2=2. (3)由b=20及a=b知a=20,由c=30及b=c知b=30,由a=30及c=a知c=20. 类型五:循环语句的应用 【例6】设计算法求+++…+的值.要求画出程序框图,写出用基本语句编写的程序. 【解析】这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下图所示: 程序如下: s=0 k=1 DO s=s+1/(k* (k+1)) k=k+1 LOOP UNTIL k>99 PRINT s END 【点拨】(1)在用WHILE语句和UNTIL语句编写程序解决问题时,一定要注意格式和条件的表述方法,WHILE语句是当条件满足时执行循环体,UNTIL语句是当条件不满足时执行循环体. (2)在解决一些需要反复执行的运算任务,如累加求和、累乘求积等问题中应注意考虑利用循环语句来实现. (3)在循环语句中,也可以嵌套条件语句,甚至是循环语句,此时需要注意嵌套的这些语句,保证语句的完整性,否则就会造成程序无法执行. 举一反三: 【变式】下图是输出某个有限数列各项的程序框图,则该框图所输出的最后一个数据是 . 【解析】由程序框图可知,当N=1时,A=1;N=2时,A=;N=3时,A=,…,即输出各个A值的分母是以1为首项以2为公差的等差数列,故当N=50时,A==,即为框图最后输出的一个数据.故填. 类型五:求最大公约数 【例7】(1)用辗转相除法求840与1 764的最大公约数; (2)用更相减损术求440与556的最大公约数. 【解析】(1)用辗转相除法求840与1 764的最大公约数: 1 764=840×2+84, 840=84×10+0. 所以840与1 764的最大公约数是84. (2)用更相减损术求440与556的最大公约数: 556-440=116, 440-116=324, 324-116=208, 208-116=92, 116-92=24, 92-24=68, 68-24=44, 44-24=20, 24-20=4, 20-4=16, 16-4=12, 12-4=8, 8-4=4. 所以440与556的最大公约数是4. 【总结升华】(1)辗转相除法与更相减损术是求两个正整数的最大公约数的方法,辗转相除法用较大的数除以较小的数,直到大数被小数除尽结束运算,较小的数就是最大公约数;更相减损术是用两数中较大的数减去较小的数,直到所得的差和较小数相等为止,这个较小数就是这两个数的最大公约数.一般情况下,辗转相除法步骤较少,而更相减损术步骤较多,但运算简易,解题时要灵活运用. (2)两个以上的数求最大公约数,先求其中两个数的最大公约数,再用所得的公约数与其他各数求最大公约数即可. 举一反三: 【变1】求147,343,133的最大公约数. 【解析】先求147与343的最大公约数. 343-147=196, 196-147=49, 147-49=98, 98-49=49, 所以147与343的最大公约数为49. 再求49与133的最大公约数. 133-49=84, 84-49=35, 49-35=14, 35-14=21, 21-14=7, 14-7=7. 所以147,343,133的最大公约数为7. 类型六:秦九韶算法 【例8】用秦九韶算法写出求多项式f(x)=1+x+0.5x2+0.016 67x3+0.041 67x4+0.008 33x5在x=-0.2时的值的过程. 【思路点拨】秦九韶算法是我国南宋的数学家秦九韶首先提出来的. (1)特点:它通过一次式的反复计算,逐步计算高次多项式的求值问题,即将一个n次多项式的求值问题,归结为重复计算n个一次式.即. (2)具体方法如下:已知一个一元n次多项式0.当x=x0,我们可按顺序一项一项地计算,然后相加,求得. 【解析】先把函数整理成f(x)=((((0.008 33x+0.041 67)x+0.166 67)x+0.5)x+1)x+1, 按照从内向外的顺序依次进行. x=-0.2, a5=0.008 33, v0=a5=0.008 33; a4=0.041 67, v1=v0x+a4=0.04; a3=0.016 67, v2=v1x+a3=0.008 67; a2=0.5, v3=v2x+a2=0.498 27; a1=1, v4=v3x+a1=0.900 35; a0=1, v5=v4x+a0=0.819 93; 所以f(-0.2)=0.819 93. 【总结升华】秦九韶算法是多项式求值的最优算法,特点是: (1)将高次多项式的求值化为一次多项式求值; (2)减少运算次数,提高效率; (3)步骤重复实施,能用计算机操作. 秦九韶算法的原理是 . 在运用秦九韶算法进行计算时,应注意每一步的运算结果,像这种一环扣一环的运算,如果错一步,则下一步,一直到最后一步就会全部算错.同学们在计算这种题时应格外小心. 举一反三: 【变式】用秦九韶算法计算多项式在x=0.4时的值时,需做加法和乘法的次数和是( ) A.10 B.9 C.12 D.8 【答案】 C 【解析】. ∴加法6次,乘法6次, ∴6+6=12(次),故选C. 类型七:进位制 【例9】(1)试把十进制数136转化为二进制数; (2)试把十进制数1 234转化为七进制数. 【思路点拨】将k进制数转换为十进制数,关键是先写成幂的积的形式再求和,将十进制数转换为k进制数,用“除k取余法”,余数的书写是由下往上,顺序不能颠倒,k进制化为m进制(k,m≠10),可以用十进制过渡 【解析】(1)由于136=2×68+0, 68=2×34+0. 34=2×17+0. 17=2×8+1. 8=2×4+0. 4=2×2+0. 2=2×1+0. 1=2×0+1. 所以136=10001000(2). (2)1234=7×176+2, 176=7×25+1. 25=7×3+4. 3=7×0+3. 所以1234=3412(7). 【总结升华】(1)应注意搞清每一次除法中的被除数、除数,当商为零时停止除法,把每步所得的余数倒着排成一个数,就是相应的二进制数. (2)十进制数转化为七进制数与转化为二进制数的方法类似,要认真体会其原理. 举一反三: 【变式1】把十进制数89化为三进制数. 【解析】具体的计算方法如下: 89=3×29+2, 29=3×9+2, 9=3×3+0, 3=3×1+0, 1=3×0+1, 所以89(10)=10 022(3). 【变式2】在十进制中,,那么在五进制中数码2 004折合成十进制为( ) A.29 B.254 C.602 D.2 004 【答案】B 【解析】,故选B.查看更多