- 2021-06-16 发布 |
- 37.5 KB |
- 61页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一数学必修学业水平复习
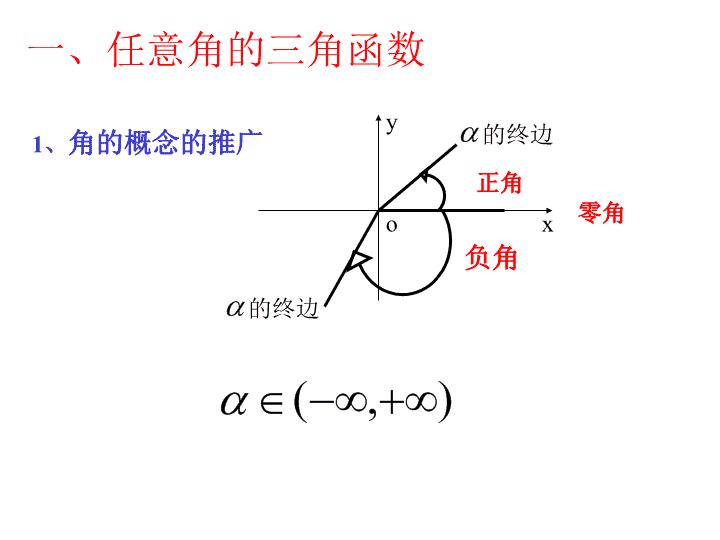
三角函数复习 一、任意角的三角函数 1、角的概念的推广 正角 负角 o x y 的终边 的终边 ),( 零角 3、象限角: 注:如果角的终边在坐标轴上,则该角不是象限角。 4、所有与角 终边相同的角,连同角 在内,构成集合: { | 360 , }S k k Z { | 2 , }k k Z (角度制) (弧度制) 例1、求在 到 ( )范围内,与下列各角终边相同的角0 360 0 2到 1 950 12 2 ()、 19( )、3 48129 1 3 原点 x轴的非负半轴 2、在直角坐标系内讨论角,角的顶点与 重合,角的始边 与 重合。逆时针旋转为正,顺时针旋转为负。 角的终边(除端点外)在第几象限,我们就说这 个角是第几象限角。 1、终边相同的角与相等角的区别 终边相同的角不一定相等,相等的角终边一定相同。 2、象限角、象间角与区间角的区别 Zkkk 2,2 x y O x y O x y O x y O 3、角的终边落在“射线上”、“直线上”及“互相 垂直的两条直线上”的一般表示式 Zkk 2 Zkk Zkk 2 二、终边相同的角 (1)与 角终边相同的角的集合: 1.几类特殊角的表示方法 { | =2k+, k∈Z}. (2)象限角、象限界角(轴线角) ①象限角 第一象限角: 2k<<2k+ , kZ 2 第二象限角: 2k+ <<2k+, kZ 2 第三象限角: 2k+<<2k+ , kZ2 3 第四象限角: 2 2k+ <<2k+2, kZ 或 2k- <<2k, kZ2 3 三、角的基本概念 ②轴线角 x 轴的非负半轴: =k360º(2k) (kZ); x 轴的非正半轴: =k360º+180º(2k+) (kZ); y 轴的非负半轴: =k360º+90º(2k+ )(kZ); 2 y 轴的非正半轴: =k360º+270º(2k+ ) 或 =k360º-90º(2k- )(kZ); 2 3 2 x 轴: =k180º(k)(kZ); y 轴: =k180º+90º(k+ )(kZ); 2 坐标轴: =k90º( )(kZ). 2 k 例2、(1)、终边落在x轴上的角度集合: (2)、终边落在y轴上的角度集合: (3)、终边落在象限平分线上的角度集合: { | , }k k Z { | , }2 k k Z { | , }4 2 k k Z 2、什么是1弧度的角? 长度等于半径长的弧所对的圆心角。 O A B r r 2r O A B r 度 弧度 0 0 30 6 45 4 3 60 2 120 3 2 135 4 3 150 6 5 270 2 3 180 360 2 90 2、角度与弧度的互化 3602 180 1801 185730.57)180(1 , 弧度 特殊角的角度数与弧度数的对应表 1)、角度与弧度的换算.只要记住,就可以方便 地进行换算. 应熟记一些特殊角的度数和弧度数. 在书写时注意不要同时混用角度制和弧度制 rad 1180180 rad1801 30.571801 rad 2)、弧长公式和扇形面积公式. rl rnrnl 1802 360 rlrrS 2 1 2 1 2 22 22 360360 rnrnS 注意: (1)圆心在原点,半径为单位长的圆叫单位圆.在 平面直角坐标系中引进正弦线、余弦线和正切线 三角函数 三角函数线 正弦函数 余弦函数 正切函数 正弦线MP 正弦、余弦函数的图象 y xxO-1 P M A(1,0) T sin=MP cos=OM tan=AT 注意:三角 函数线是有 向线段! 余弦线OM 正切线AT 为第二象限角时 为第一象限角时 为第三象限角时 为第四象限角时 sin cos sin , ,y r cos ,x r x y o 0 1 -1 0 + +_ _ 1 0 0 -1 x y o + + _ _ 不存在 x y o 0 0 不存在 _ +_ + tan ,y x tan 一、任意角的三角函数定义 x y o ● P(x,y) r 的终边 sin ,cos ,tany x y r r x = = = 二、同角三角函数的基本关系式 商关系: sintan cos = 平方关系: 2 2sin cos 1 + = 22 yxr 三角函数值的符号:“第一象限全为正,二正三切四余弦” 设00900,对于任意一个00到3600的角 = , 当[00,900] 1800-, 当[900,1800] 1800+,当[1800,2700] 3600-,当[2700,3600] 如何求非锐角的三角函数值呢? 角1800-, 1800+, 3600-的三角函数值与 的三角函数值有何关系呢? sin)2sin( k cos)2cos( k tan)2tan( k -sinsin( ) -coscos( ) tantan( ) sinsin( ) -coscos( ) tantan( ) -sinsin( ) coscos( ) tantan( ) (注意:把 看作是锐角) sin( ) cos2 cos( ) sin2 tan( ) cot2 sin( ) cos2 cos( ) sin2 tan( ) cot2 公式五: 公式六: 偶同奇余 象限定号 利用诱导公式把任意角的三角函数转化为锐角三角 函数,一般按下面步骤进行: 任意负角的 三角函数 任意正角的 三角函数 锐角三 角函数 到 的角 的三角函数 o0 o360 用公式三或一 用公式一 用公式 二或四 你记住了吗? 度 弧 度 00 030 045 060 090 0120 0135 0150 0180 0270 0360 0 6 4 3 2 2 3 3 4 5 6 3 2 2 sin cos tan cot 2 1 2 3 3 3 3 2 1 2 3 3 3 3 2 1 2 3 3 3 3 2 1 2 3 3 3 3 1 1 2 2 2 2 1 1 2 2 2 20 0 1 0 0 10 0 1 0 0 1 0 1 0 三、三角函数图像和性质 函数 y=sinx y=cosx y=tanx 图象 定义 值域 奇偶性 对称 中心 2 kx 0,k 0,2 k 0,2 k R R [-1,1] [-1,1] R 奇 奇偶 y=sinx y=cosx y=tanx { | , }2x x k k Z )(22,22 Zkkk )(2 32,22 Zkkk )(2,2 Zkkk )(2,2 Zkkk )(2,2 zkkk ))(0,( Zkk )(2 Zkkx )( Zkkx ))(0,2( Zkk ))(0,2( Zkk 2T 2T T 定义域 值域 奇偶性 单调性 周期性 对称性 R R R[-1,1] [-1,1] 奇函数 奇函数偶函数 增区间: 增区间: 增区间: 减区间: 减区间: 对称中心: 对称中心: 对称中心: 对称轴: 对称轴: . y=sinx y x 1 -1 /2 2 o 3/2 . ... 五点作图法 . /2 3/2 2 o y x y=cosx . . .1 -1 对称点:(k,0) 对称轴:x=k+ 2 对称轴:x=k 对称点:(k+ ,0) 2 T/2 k∈Z k∈Z T/2 正切函数的性质: 6、对称性:对称中心 ( ,0)2 k xO y 1 1 2 2 3 2 2 2 3 4 1y 1y 7、渐进线: 2x k 1、作y=Asin(ωx+φ)图象的方法 法一:五点法 法二:图象变换法 (1)振幅变换(对A) (2)周期变换(对ω) (3)相位变换(对φ) (二) y=Asin(ωx+φ)的相关问题 1、先由图象确定A与T 2、由ω= 2 T 求ω 3、特殊点代入法求 对称轴:ωx+=k+ 2 x= 2k+-2 2ω 对称中心: k- ω ,0 k为整数 3、求y=Asin(ωx+φ)+K 的解析式的方法 4、y=Asin(ωx+φ)(A>0,ω>0) 的图象的对称中心 和对称轴方程 )sin( xAy xy sin 0 0 || )sin( xy 1 10 1 )sin( xy )sin( xAy xy sin 10 1 1 xy sin 0 0 || )sin( xy )sin( xAy )的简图.Asin(ωx1.五点法作函数y 的思想.看图说话3." " )的图象.Asin(ωx函数y2.通过图象变换得到 时 "的思想.代点看趋4. " 势求解析式 注意 sin( )y A x B 函数系列要求: sin( )y A x B 十二、两角和与差的正弦、余弦、正切: ( ) :S ( ) :S ( ) :C ( ) :C ( )T ( ) :T sin( ) sin cos cos sin sin( ) sin cos cos sin cos( ) cos cos sin sin cos( ) cos cos sin sin tan tantan( ) 1 tan tan tan tantan( ) 1 tan tan ( )T ( )T 如: ( ) ,2 ( ) ( ) 2 ( ) ( ),2 ( ) 3 6 与 互余, + 与 互余4 4 3、倍角公式 cossin22sin 22 sincos2cos 22 sin211cos2 1sincos 22 2tan1 tan22tan 注:正弦与余弦的倍角公式的逆用实质上就是降幂的过程。特别 2 2cos1cos2 2 2cos1sin 2 返回 和角公式的一个重要变形 ]cos,sin[ )sin(cossin 2222 22 ba a ba b xbaxbxa 其中 21 cos cos2 2 21 cos sin2 2 2 1 cos2sin 2 2 1 cos2cos 2 降 幂 ( 扩 角 ) 公 式 升 幂 ( 缩 角 ) 公 式 和差化积公式: 积化和差公式: 1sin cos [sin( ) sin( )]2 1cos sin [sin( ) sin( )]2 1cos cos [cos( ) cos( )]2 1sin sin [cos( ) cos( )]2 sin sin 2sin cos2 2 cos cos 2sin sin2 2 sin sin 2cos sin2 2 cos cos 2cos cos2 2 找出非特殊角和特殊角之间的关系, 这种技巧在化简求值中经常用到,并且 三角式变形有规律即坚持“二化”: 多角同角化 异名同名化 山东学业水平测试题 • 1.(08年3).若点P(-1,2)在角的终边上,则tan 等于 A. -2 B. C. D. • 2.(08年6).为了得到函数y=sin(2x- )(X R)的图像, 只需把函数 y=sin2x 的图像上所有的点 ( ) A.向右平移 个单位长度 B.向右平移 个单位长度 C.向左平移 个单位长度 D.向左平移 个单位长度 5 5 2 1 5 52 A 3 3 3 6 6 B 山东学业水平测试题 3、(2010 山东 7T) 4、(2010 山东 1月 9T) 在ΔABC中,sinAsinB-cosAcosB<0则这个三角形一定是 A 锐角三角形 B 钝角三角形 C 直角三角形 D 等腰三角形 B B 山东学业水平测试题 5、 6、 D B 山东学业水平测试题 7、 C 山东学业水平测试题 (2013 12月 山东 2T) ( ) 8、 9、 ,0 B 山东学业水平测试题 (2013 12月 山东 3T) (2013 12月 山东 10T) 10、 11、 B C 山东学业水平测试题 (2013 12月 山东 14T) (2013 12月 山东 18T) 12、 13、 D A 山东学业水平测试题 (2013 12月 山东 25T) (2013 山东 1月 3T) 14、 15、 c o s 9 A 山东学业水平测试题 (2013 山东 1月 10T) (2011 山东 1月 5T) 的值为 A. 0 B. C. D. 1 1 2 3 2 0 0 0 0cos75 cos15 sin 75 sin15 17、 16、 D B 山东学业水平测试题 (2013 山东 1月 13T)18、 C 山东学业水平测试题 (2011 山东 1月 10T) 已知函数 ,下面结论正确 的是( ) A. 函数 的最小正周期为 B. 函数 在区间 上是增函数 C. 函数 是奇函数 D. 函数 的图象关于直线 对称 ( ) sin( )( )2f x x x R 2 [0, ]2 0x ( ) sin( )( )2f x x x R ( ) sin( )( )2f x x x R ( ) sin( )( )2f x x x R ( ) sin( )( )2f x x x R 19、 D 山东学业水平测试题 (2011 山东 1月 19T) 已知 ,则 等于 。3sin , ( , )5 2 sin 2 (2010 山东 1T) 20、 21、 25 24 D 山东学业水平测试题 • 22、(08年21).(本小题满分6分) 求函数f(x)=2sin(x+ )-2cosx的最大值。6 xxxxxxf cossin3cos2)cos2 1sin2 3(2)( 6 6 解: = 2sin(x- ) . ∵ -1≤sin(x- )≤1 ∴ f (x)max = 2 . 平面向量学业水平复习 高一数学(必修4) 一.基本概念 1.向量及向量的模、向量的表示方法 1)图形表示 2)字母表示 3)坐标表示 A B a AB 有向线段AB :| | | |a AB 向量的模 ( , )a xi y j x y ( , ) ( , )a OA x y A x y 点 ( , )B A B Aa AB x x y y 一.基本概念 2.零向量及其特殊性 3.单位向量 (1)0 / /a (2) 0 (3)0 a 0 0 | | 1a 4.平行向量,相等向量,相反向量 5.两个非零向量 的夹角a b 与 [0, ] 二.基本运算 AB BC AC ( )a R a 向量 与 共线 AB AC CB a b a b a 1. 向量线性运算 2.两个非零向量 的数量积a b 与 a b | | | | cosa b b a 叫做向量 在 方向上的投影| | cosb 1 1 2 2( , ), ( , ), 1) 2) 3) 4) a x y b x y a b a b a a b 若 则 )yy,xx( 2121 )yy,xx( 2121 )y,x( 11 二.基本运算(坐标途径) 2121 yyxx 5) | | 6)cos | || | a a a a b a b 2 1 2 1 yx 2 2 2 2 2 1 2 1 2121 yxyx yyxx 1. / / b a b a 向量 和非零向量 2. a b 非零向量 和 则若 ),y,x(b),y,x(a 2211 0yxyx 1221 0yyxx 2121 三.两个等价条件 b a 有唯一的实数 ,使 0a b a b 四.一个基本定理 2.平面向量基本定理 . ee eea,, ,a, ee 21 221121 21 基底平面内所有向量的一组 叫做表示这一、把不共线的向量 使有且只有一对实数 任一向量那么对于这一平面内的向量 共线的是同一平面内的两个不、如果 利用向量分解的“唯一性”来构建实系数方程组 山东学业水平测试题 • 1、(08年19)、设 且 的夹 角为钝角,则x的取值范围是___________. • 2、(10年20)、设┃a┃=12,┃b┃=9, a b= -54 , 则a和 b的夹角θ为______. ),5,3(),2,( bxa ba ,10- 3 6 5 X> 且x≠ 2 4 3 山东学业水平测试题 3、 4、 C C 山东学业水平测试题 (2013 12月 山东 6T) (2013 12月 山东 8T) 5、(1) 5、(2) B B 山东学业水平测试题 (2013 12月山东 22T) (2013 1月 山东 21T)6、(2) 6、(1) 3 2 )4,2( � 山东学业水平测试题 (2013 1月 山东 26T) 间.的最大 值最大值及单调 ,求 设函数3,1 ,3,sin1 已知向量 f(x)baf(x) bxa 7、 山东学业水平测试题 (2011 1月 山东 4T) 已知向量 ,则 的坐标为 A. (-5,3) B.(-1,5) C.(5,-3) D.(1,-5) (2,1), ( 3,4)a b a b 8、 C 山东学业水平测试题 • (10年 24题 8分) 已知函数 求f(x)的最大值,并求使f(x)取得最大值时x 的集合 9、 Rxxxxf ,cos2 1sin2 3)( 山东学业水平测试题 (2011 1月 山东 22T 6分) 已知平面向量 ,设 函数 ,求函数 的最大值及取 最 大值时 的值。 解: 当 即 时,函 数 取得最大值 (1, 3), (cos ,sin )a b x x ( )f x a b ( )f x a b x 10、 xxxxbaxf sin3cos)sin,(cos)3,1()( )6sin(2)sin2 3cos2 1(2 xxx 226 kx 32 kx )(xf 2. 山东学业水平测试题 (2011 1月 山东 25T 8分) 已知平面上两点 ,动点 满足 (1)求动点 的轨迹C的方程。 (2)若点 是轨迹C内一点,过点Q任作直线 交轨迹C于A,B两点,使证: 的值只与 有关; 令 ,求 的取值范围。 (4,0), (1,0)M N P | | 2 | |PM PN P ( ,0)Q a l QA QB a ( )f a QA QB ( )f a QA QB 11、查看更多