【数学】2020届一轮复习人教版(理)第2章第4讲二次函数与幂函数作业
A组 基础关
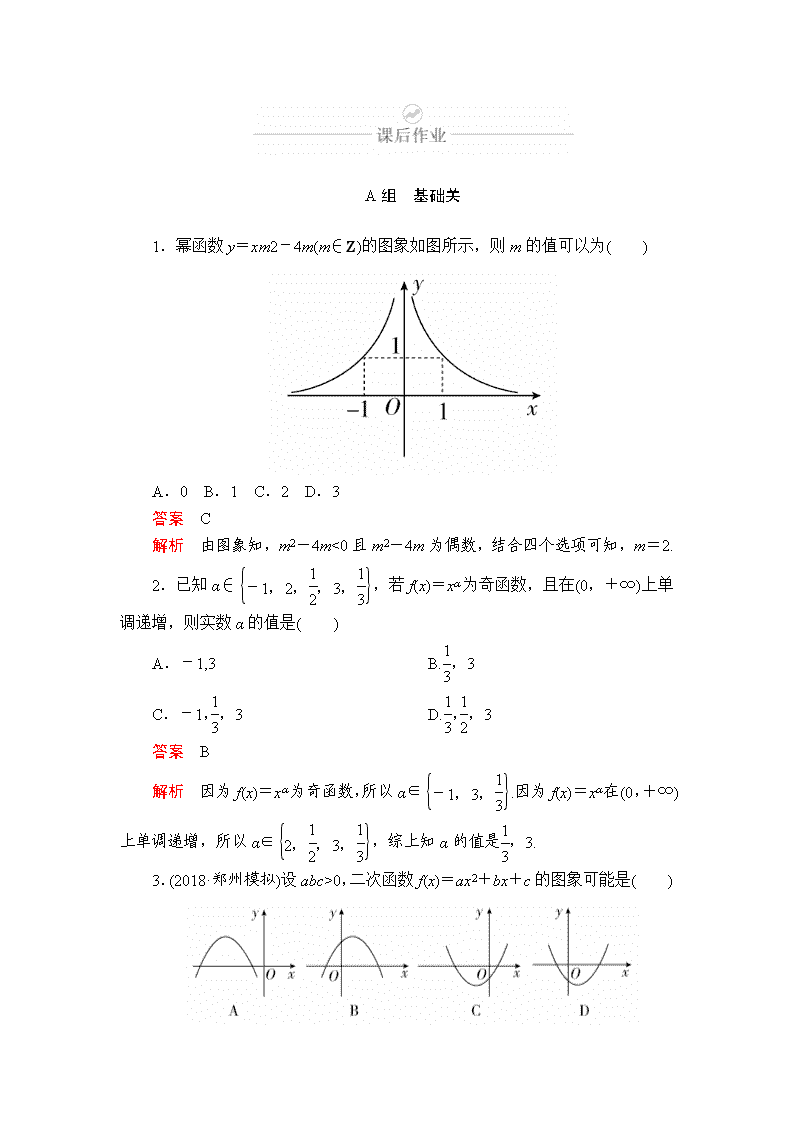
1.幂函数y=xm2-4m(m∈Z)的图象如图所示,则m的值可以为( )
A.0 B.1 C.2 D.3
答案 C
解析 由图象知,m2-4m<0且m2-4m为偶数,结合四个选项可知,m=2.
2.已知α∈,若f(x)=xα为奇函数,且在(0,+∞)上单调递增,则实数α的值是( )
A.-1,3 B.,3
C.-1,,3 D.,,3
答案 B
解析 因为f(x)=xα为奇函数,所以α∈.因为f(x)=xα在(0,+∞)上单调递增,所以α∈,综上知α的值是,3.
3.(2018·郑州模拟)设abc>0,二次函数f(x)=ax2+bx+c的图象可能是( )
答案 D
解析 由A中图象知,a<0,c<0,-<0,所以b<0,与abc>0矛盾;
由B中图象知,a<0,c>0,->0,所以b>0,与abc>0矛盾;
由C中图象知,a>0,c<0,-<0,所以b>0,与abc>0矛盾;
由D中图象知,a>0,c<0,->0,所以b<0,abc>0成立.
4.(2018·安阳模拟)下列选项正确的是( )
A.0.20.2>0.30.2 B.2<3
C.0.8-0.1>1.250.2 D.1.70.3>0.93.1
答案 D
解析 y=x0.2在(0,+∞)上为增函数,且0.2<0.3,所以0.20.2<0.30.2,故A错误;
y=x在(0,+∞)上为减函数,且2<3,所以2>3,故B错误;
因为0.8-0.1=1.250.1<1.250.2,故C错误;
因为1.70.3>1.70=1,0.93.1<0.90=1,所以1.70.3>0.93.1,故D正确.
5.(2018·福建三明一中模拟)已知函数f(x)=(x-1)·(ax+b)为偶函数,且在(0,+∞)上单调递减,则f(3-x)<0的解集为( )
A.(2,4) B.(-∞,2)∪(4,+∞)
C.(-1,1) D.(-∞,-1)∪(1,+∞)
答案 B
解析 因为函数f(x)=(x-1)(ax+b)为偶函数,且在(0,+∞)上单调递减,所以f(x)在(-∞,0)上单调递增,又因为f(1)=0,
所以由f(3-x)<0得f(|3-x|)
1,解得x>4或x<2,
所以f(3-x)<0的解集为(-∞,2)∪(4,+∞).
6.已知函数f(x)=ax2+x+5的图象在x轴上方,则a的取值范围是( )
A. B.
C. D.
答案 C
解析 ∵函数f(x)=ax2+x+5的图象在x轴上方,
∴解得a>.
7.已知二次函数f(x)=2ax2-ax+1(a<0),若x1f(x2)
C.f(x1)0,
∴x2-<-x1,∴f(x1)0时,图象开口向上,
所以当x=2时取得最大值,即f(2)=4a+4a+1=4,
解得a=;
当a<0时,图象开口向下,
所以当x=-1时取得最大值,即f(-1)=a-2a+1=4,解得a=-3.
B组 能力关
1.若关于x的不等式x2-4x-2-a>0在区间(1,4)内有解,则实数a的取值范围是( )
A.(-∞,-2) B.(-2,+∞)
C.(-6,+∞) D.(-∞,-6)
答案 A
解析 令f(x)=x2-4x-2-a,则函数的图象为开口向上且以直线x=2为对称轴的抛物线,故在区间(1,4)上,f(x)0在区间(1,4)内有解,则-2-a>0,解得a<-2.
2.为了美观,在加工太阳镜时将下半部分轮廓制作成二次函数图象的形状(如图所示).若对应的两条曲线关于y轴对称,AE∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm,则右轮廓线DFE所在的二次函数的解析式为( )
A.y=(x+3)2 B.y=(x-3)2
C.y=(x+3)2 D.y=(x-3)2
答案 D
解析 ∵高CH=1 cm,BD=2 cm,且B,D关于y轴对称,
∴D点坐标为(1,1),∵AB∥x轴,AB=4 cm,
最低点C在x轴上,∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(-3,0),
∴右边抛物线的顶点F的坐标为(3,0),
设右边抛物线的解析式为y=a(x-3)2,
把D(1,1)代入得1=a×(1-3)2,解得a=,
∴右边抛物线的解析式为y=(x-3)2.
3.(2018·天津高考)已知a∈R,函数f(x)=
若对任意x∈[-3,+∞),f(x)≤|x|恒成立,则a的取值范围是________.
答案
解析 当-3≤x≤0时,由f(x)≤|x|得,x2+2x+a-2≤-x.即a≤-x2-3x+2,而-x2-3x+2的最小值为2,所以a≤2.当x>0时,由f(x)≤|x|得,-x2+2x-2a≤x.即2a≥-x2+x,而-x2+x的最大值为,所以a≥.
综上可知,≤a≤2.
4.已知函数f(x)=ax2-2ax+2+b(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-mx在[2,4]上单调,求m的取值范围.
解 (1)f(x)=a(x-1)2+2+b-a.
当a>0时,f(x)在[2,3]上为增函数,
故⇒⇒
当a<0时,f(x)在[2,3]上为减函数,
故⇒⇒
故当a>0时,a=1,b=0,当a<0时,a=-1,b=3.
(2)∵b<1,∴a=1,b=0,即f(x)=x2-2x+2.
g(x)=x2-2x+2-mx=x2-(2+m)x+2,
∵g(x)在[2,4]上单调,∴≤2或≥4.
∴m≤2或m≥6.
故m的取值范围为(-∞,2]∪[6,+∞).
5.若二次函数f(x)=ax2+bx+c(a≠0)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
解 (1)由f(0)=1,得c=1,所以f(x)=ax2+bx+1.
又f(x+1)-f(x)=2x,
所以a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
即2ax+a+b=2x,所以所以
因此,所求解析式为f(x)=x2-x+1.
(2)f(x)>2x+m等价于x2-x+1>2x+m,即x2-3x+1-m>0,要使此不等式在区间[-1,1]上恒成立,只需使函数g(x)=x2-3x+1-m在区间[-1,1]上的最小值大于0即可.
因为g(x)=x2-3x+1-m在区间[-1,1]上单调递减,所以g(x)min=g(1)=-m-1,由-m-1>0,得m<-1.因此满足条件的实数m的取值范围是(-∞,-1).