【数学】2020届一轮复习人教A版空间向量在立体几何中的应用学案

【数学】2020届一轮复习人教A版空间向量在立体几何中的应用学案

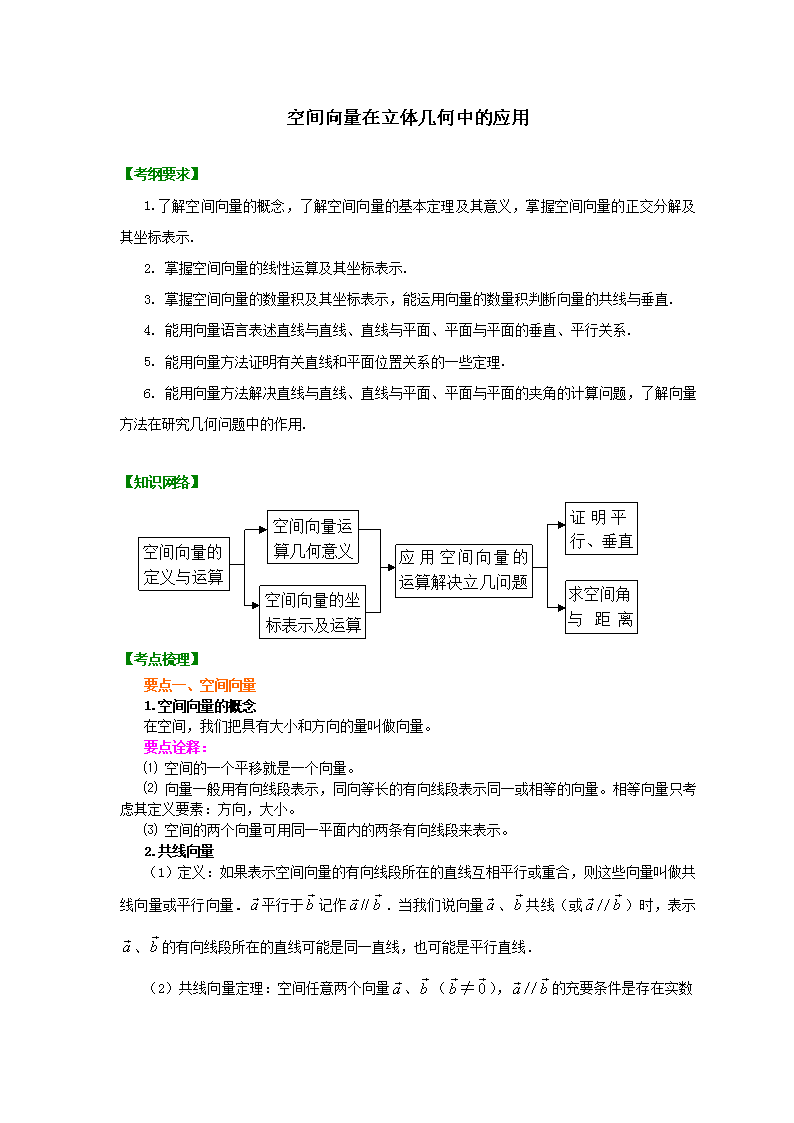
空间向量在立体几何中的应用 ‎ ‎ ‎【考纲要求】‎ ‎1.了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示.‎ ‎2. 掌握空间向量的线性运算及其坐标表示.‎ ‎3. 掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直.‎ ‎4. 能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.‎ ‎5. 能用向量方法证明有关直线和平面位置关系的一些定理.‎ ‎6. 能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题，了解向量方法在研究几何问题中的作用.‎ ‎【知识网络】‎ ‎【考点梳理】‎ 要点一、空间向量 ‎1.空间向量的概念 在空间，我们把具有大小和方向的量叫做向量。‎ 要点诠释：‎ ‎⑴ 空间的一个平移就是一个向量。‎ ‎⑵ 向量一般用有向线段表示，同向等长的有向线段表示同一或相等的向量。相等向量只考虑其定义要素：方向，大小。‎ ‎⑶ 空间的两个向量可用同一平面内的两条有向线段来表示。‎ ‎2.共线向量 ‎（1）定义：如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量．平行于记作．当我们说向量、共线（或//）时，表示、的有向线段所在的直线可能是同一直线，也可能是平行直线．‎ ‎（2）共线向量定理：空间任意两个向量、（≠），//的充要条件是存在实数 λ，使＝λ。‎ ‎3.向量的数量积 ‎（1）定义：已知向量，则叫做的数量积，记作，即 ‎。‎ ‎（2）空间向量数量积的性质：‎ ‎① ；‎ ‎② ；‎ ‎③ ．‎ ‎（3）空间向量数量积运算律：‎ ‎①；‎ ‎②（交换律）；‎ ‎③（分配律）。‎ ‎4.空间向量基本定理 如果三个向量不共面，那么对空间任一向量，存在一个唯一的有序实数组，使。若三向量不共面，我们把叫做空间的一个基底，叫做基向量，空间任意三个不共面的向量都可以构成空间的一个基底。‎ ‎5.空间直角坐标系：‎ ‎（1）若空间的一个基底的三个基向量互相垂直，且长为，这个基底叫单位正交基底，用表示；‎ ‎（2）在空间选定一点和一个单位正交基底，以点为原点，分别以的方向为正方向建立三条数轴：轴、轴、轴，它们都叫坐标轴．我们称建立了一个空间直角坐标系，点叫原点，向量 都叫坐标向量．通过每两个坐标轴的平面叫坐标平面，分别称为平面，平面，平面；‎ ‎6.空间直角坐标系中的坐标 ‎ 在空间直角坐标系中，对空间任一点，存在唯一的有序实数组，使，有序实数组叫作向量在空间直角坐标系中的坐标，记作，叫横坐标，叫纵坐标，叫竖坐标．‎ ‎7.空间向量的直角坐标运算律：‎ ‎（1）若，，则．‎ 一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。‎ ‎（2）若，，则 ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎；‎ ‎，．‎ 夹角公式：．‎ ‎（3）两点间的距离公式：若，，则 或 。‎ 要点二、空间向量在立体几何中的应用 ‎1. 立体几何中有关垂直和平行的一些命题，可通过向量运算来证明．‎ 对于垂直问题，一般是利用进行证明；‎ 对于平行问题，一般是利用共线向量和共面向量定理进行证明．‎ ‎2.利用向量求夹角(线线夹角、线面夹角、面面夹角)有时也很方便．其一般方法是将所求的角转化为求两个向量的夹角或其补角，而求两个向量的夹角则可以利用向量的夹角公式。‎ 要点诠释：‎ 平面的法向量的求法：‎ 设n=(x,y,z)，利用n与平面内的两个不共线的向a，b垂直，其数量积为零，列出两个三元一次方程，联立后取其一组解，即得到平面的一个法向量（如图）。‎ 线线角的求法：‎ 设直线AB、CD对应的方向向量分别为a、b，则直线AB与CD所成的角为。（注意：线线角的范围[00,900]）‎ 线面角的求法：‎ 设n是平面的法向量，是直线的方向向量，则直线与平面所成的角为（如图）。‎ 二面角的求法：‎ 设n1，n2分别是二面角的两个面，的法向量，则就是二面角的平面角或其补角的大小（如图）‎ ‎3.用向量法求距离的公式 设n是平面的法向量，AB是平面的一条斜线，则点B到平面的距离为（如图）。‎ 要点诠释：‎ ‎⑴ 点A到平面的距离：‎ ‎，其中，是平面的法向量。‎ ‎⑵ 直线与平面之间的距离：‎ ‎，其中，是平面的法向量。‎ ‎⑶ 两平行平面之间的距离：‎ ‎，其中， 是平面的法向量。‎ ‎【典型例题】‎ 类型一、空间向量的运算 ‎【例1】已知=（2，2，1），=（4，5，3），求平面ABC的单位法向量。‎ ‎【答案】单位法向量=±（，－，）.‎ ‎【解析】设面ABC的法向量，则⊥且⊥，即 ‎，即，解得，‎ 令，则 ‎∴单位法向量=±（，－，）.‎ ‎【总结升华】一般情况下求法向量用待定系数法。由于法向量没规定长度，仅规定了方向，所以有一个自由度，可把的某个坐标设为1，再求另两个坐标。平面法向量是垂直于平面的向量，故法向量的相反向量也是法向量，所以本题的单位法向量应有两解。‎ 举一反三：‎ ‎【变式】若＝(1,5,－1)，＝(－2,3,5)‎ ‎（1）若，求实数k的值；‎ ‎（2）若，求实数k的值；‎ ‎（3）若取得最小值，求实数k的值。‎ ‎【答案】‎ ‎(1)‎ ‎，即 由，解得； ‎ ‎(2)，‎ ‎，‎ 即，解得；‎ ‎(3) ‎ 当时，取得最小值。‎ 类型二：向量法证明平行或垂直 ‎【例2】如图，在四棱锥中，底面四边长为1的菱形，, , ,为的中点，为的中点 ‎（Ⅰ）证明：直线；‎ ‎（Ⅱ）求异面直线AB与MD所成角的大小； ‎ ‎（Ⅲ）求点B到平面OCD的距离。‎ ‎【解析】作于点P,如图,分别以AB,AP,AO所在直线为轴建立坐标系 ‎,‎ ‎(1)‎ 设平面OCD的法向量为,则 即 ‎ 取,解得 ‎(2)设与所成的角为,‎ ‎ , 与所成角的大小为 ‎(3)设点B到平面OCD的距离为,则为在向量上的投影的绝对值,‎ 由 , 得.‎ 所以点B到平面OCD的距离为 ‎【总结升华】1. 用向量证明线面平行的方法有：‎ ‎(1)证明该直线的方向向量与平面的某一法向量垂直；‎ ‎(2)证明该直线的方向向量与平面内某直线的方向向量平行；‎ ‎(3)证明该直线的方向向量可以用平面内的两个不共线的向量线性表示．‎ ‎2. 用向量法证垂直问题：‎ ‎(1)证明线线垂直，只需证明两直线的方向向量数量积为0；‎ ‎(2)证明线面垂直，只需证明直线的方向向量与平面的法向量共线，或利用线面垂直的判定定理转化为证明线线垂直；‎ ‎(3)证明面面垂直，只需证明两平面的法向量的数量积为0，或利用面面垂直的判定定理转化为证明线面垂直．‎ 举一反三：‎ ‎【变式】ID 401056【高清视频空间向量在立体几何中的应用例题1】如图，已知直三棱柱ABC－A1B1C1中，△ABC为等腰直角三角形，∠BAC＝90°，且AB＝AA1，D、E、F分别为B1A、C1C、BC的中点．求证：‎ ‎(1)DE∥平面ABC；‎ ‎(2)B1F⊥平面AEF.‎ ‎【解析】如图建立空间直角坐标系A－xyz，令AB＝AA1＝4，‎ 则A(0，0，0)，E(0，4，2)，F(2，2，0)，B(4，0，0)，B1(4，0，4)．‎ ‎(1)取AB中点为N，则N(2，0，0)，C(0，4，0)，D(2，0，2)，‎ ‎∴＝(－2，4，0)，＝(－2，4，0)，‎ ‎∴＝.∴DE∥NC，‎ 又NC在平面ABC内，DE不在平面ABC内，故DE∥平面ABC.‎ ‎(2)＝(－2，2，－4)，＝(2，－2，－2)，‎ ＝(2，2，0)，‎ ·＝(－2)×2＋2×(－2)＋(－4)×(－2)＝0，‎ 则⊥，∴B1F⊥EF，‎ ‎∵·＝(－2)×2＋2×2＋(－4)×0＝0.‎ ‎∴⊥，即B1F⊥AF，‎ 又∵AF∩FE＝F，∴B1F⊥平面AEF.‎ 类型三：异面直线所成的角 ‎【例3】正方体ABCD-EFGH的棱长为a，点P在AC上，Q在BG上，且AP=BQ=a, 求直线PQ与AD所成的角 ‎【答案】90°‎ ‎【解析】建立空间直角坐标系如图，则，‎ ‎,‎ ‎∴,，‎ ‎∴‎ ‎∴QP与AD所成的角为90°。‎ ‎【总结升华】建立坐标系后，求出 可由求解。‎ 举一反三：‎ ‎【变式】如图，在直四棱柱中，底面是边长为的菱形，侧棱长为 ‎（1）与能否垂直？请证明你的判断；‎ ‎（2）当在上变化时，求异面直线与所成角的取值范围。‎ ‎【答案】∵菱形中，于，设，‎ 分别以所在直线为轴，建立空间直角坐标系，‎ 设，则 ‎（1）∵，‎ ‎∴，∴与不能垂直。‎ ‎（2）∵，∴，∵‎ ‎∴，‎ ‎，‎ ‎∵，∴设，‎ 又，∴‎ ‎∵，∴‎ ‎∴直线与所成角的取值范围是。‎ 类型四：直线与平面所成的角 ‎【例4】如图，在棱长为1的正方体中，是侧棱上的一点，。试确定，使直线与平面所成角的正切值为；‎ ‎【解析】建立如图所示的空间直角坐标系，‎ 则A(1,0,0),B(1,1,0),P(0,1,ｍ)，C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1).‎ 所以 又由的一个法向量.‎ 设与所成的角为，‎ 则 依题意有，解得.‎ 故当时，直线。‎ 举一反三：‎ ‎【变式】如图，三棱锥P-ABC中，∠ABC=，PA=1，AB=，AC=2，PA⊥面ABC．‎ ‎(1)求直线AB和直线PC所成角的余弦值；‎ ‎(2)求PC和面ABC所成角的正弦值；‎ ‎【答案】 ‎ ‎(1)以A为坐标原点，分别以AB、AP所在直线为y轴、z轴,以过A点且平行于BC直线为x轴建立空间直角坐标系.‎ 在直角△ABC中,∵AB=，AC=2，∴BC=1‎ A(0,0,0)，B(0,,0)，C(1,,0)，P(0,0,1).‎ ‎(0,,0)，(1,,),‎ cos<,>===‎ ‎∴直线AB与直线PC所成的角余弦为.‎ ‎(2)取平面ABC的一个法向量=(0，0，1)，‎ 设PC和面ABC所成的角为，则 sin=|cos<，>|==.‎ ‎∴PC和面ABC所成的角的正弦值为．‎ 类型五：二面角 ‎【例5】 ID 401056 【高清视频空间向量在立体几何中的应用例题2】如图，在三棱柱ABC－A1B1C1中，H是正方形AA1B1B的中心，AA1＝2，C1H⊥平面AA1B1B，且C1H＝.‎ ‎(1)求异面直线AC与A1B1所成角的余弦值；‎ ‎(2)求二面角A－A1C1－B1的正弦值；‎ ‎(3)设N为棱B1C1的中点，点M在平面AA1B1B内，且MN⊥平面A1B1C1，求线段BM的长．‎ ‎【解析】如图所示，建立空间直角坐标系，点B为坐标原点，依题意得A(2，0，0)，B(0，0，0)，C(，－，)，A1(2，2，0)，B1(0，2，0)，C1(，，)．‎ ‎(1)易得＝(－，－，)，＝(－2，0，0)，‎ 于是cos〈，〉＝＝＝，‎ 所以异面直线AC与A1B1所成角的余弦值为.‎ ‎(2)易知＝(0，2，0)，＝(－，－，)．‎ 设平面AA1C1的一个法向量m＝(x，y，z)，则 即不妨令x＝，可得m＝(，0，)．‎ 设平面A1B1C1的一个法向量n＝(x，y，z)，则 即不妨令y＝，可得n＝(0，，)．‎ 则cos〈m，n〉＝＝＝，从而sin〈m，n〉＝，‎ 所以二面角A－A1C1－B1的正弦值为.‎ ‎(3)由N为棱B1C1的中点，得N(，，)．设M(a，b，0)，‎ 则＝(－a，－b，)．因为MN⊥平面A1B1C1，‎ 由(2)知平面A1B1C1的一个法向量为n＝(0，，)，所以∥n，‎ 所以－a＝0，＝，‎ 解得.故M(，，0)．因此＝(，，0)，所以线段BM的长||＝.‎ ‎【总结升华】求两异面直线所成的角，用向量法就是求两直线上的两方向向量的夹角，但需注意二者范围的区别．同样地，利用向量法求二面角的大小，就是求两个半平面的法向量的夹角(或夹角的补角)，在具体求解中应适当选取或求解直线的方向向量及平面的法向量．在空间直角坐标系中，常采用待定系数法求平面的法向量．‎ 举一反三：‎ ‎【变式】如图，矩形ABCD和梯形BEFC所在平面互相垂直，BE∥CF，∠BCF=∠CEF=90°，，EF=2。‎ ‎（Ⅰ）求证：AE∥平面DCF；‎ ‎（Ⅱ）当AB的长为何值时，二面角A—EF—C的大小为60°？‎ ‎【解析】如图，以点为坐标原点，以和分别作为轴，轴和轴，建立空间直角坐标系．‎ D A B E F C y z x 设，‎ 则，，，，．‎ ‎（Ⅰ）证明：，，，‎ 所以，，从而，，‎ 所以平面．‎ 因为平面，所以平面平面．‎ 故平面．‎ ‎（Ⅱ）解：因为，，‎ 所以，，从而 解得．所以，．‎ 设与平面垂直，‎ 则，，解得．‎ 又因为平面，，‎ 所以，得到．‎ 所以当为时，二面角的大小为．‎ 类型六：空间距离 ‎【例5】如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，AB＝2.求点A到平面MBC的距离．‎ ‎【解析】‎ 取CD中点O，连接OB，OM，‎ 则OB⊥CD，OM⊥CD.‎ 又平面MCD⊥平面BCD，‎ 所以MO⊥平面BCD.‎ 取O为原点，直线OC、BO、OM为x轴、y轴、z轴，建立空间直角坐标系如图．OB＝OM＝，则各点坐标分别为C(1，0，0)，M(0，0，)，B(0，－，0)，A(0，－，2)．‎ ‎(1)设是平面MBC的法向量，则 ＝(1，，0)，＝(0，，)．‎ 由⊥得·＝0即x＋y＝0；‎ 由⊥得·＝0即y＋z＝0.‎ 取＝(，－1，1)，＝(0，0，2)，‎ 则d＝＝＝.‎ 故点A到平面MBC的距离为.‎ 法二：(1)取CD中点O，连OB，OM，‎ 则OB＝OM＝，OB⊥CD，MO⊥CD，‎ 又平面MCD⊥平面BCD，‎ 则MO⊥平面BCD，‎ 所以MO∥AB，所以MO∥平面ABC，‎ 故M，O到平面ABC的距离相等．‎ 作OH⊥BC于H，连MH，则MH⊥BC.‎ 求得OH＝OC·sin60°＝，‎ MH＝ ‎＝.‎ 设点A到平面MBC的距离为d，‎ 由VA－MBC＝VM－ABC得 ·S△MBC·d＝·S△ABC·OH.‎ 即××2×d＝××2×2×，‎ 解得d＝.‎ ‎【总结升华】利用向量法求点到平面的距离的步骤如下：(1)求出该平面的一个法向量；(2)找出以该点及平面内的某点为端点的线段对应的向量；(3)利用公式d＝求距离．‎ 举一反三：‎ ‎【变式】如图，四面体ABCD中，O、E分别是BD、BC的中点，，,求点E到平面ACD的距离。‎ ‎【答案】以O为原点，如图建立空间直角坐标系，‎ 则 设平面ACD的法向量为则 ‎，令得是平面ACD的一个法向量。‎ 又 点E到平面ACD的距离 类型七、利用空间向量解决立体几何中的探索问题 例6. （2018 湖北高考）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马P﹣ABCD中，侧棱PD⊥底面ABCD，且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE，DF，BD，BE．‎ ‎（1）证明：PB⊥平面DEF．试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；‎ ‎（2）若面DEF与面ABCD所成二面角的大小为，求的值．‎ ‎【解析】解法1）（1）因为PD⊥底面ABCD，所以PD⊥BC，‎ 由底面ABCD为长方形，有BC⊥CD，而PD∩CD=D，‎ 所以BC⊥平面PCD．而DE⊂平面PDC，所以BC⊥DE．‎ 又因为PD=CD，点E是PC的中点，所以DE⊥PC．‎ 而PC∩CB=C，所以DE⊥平面PBC．而PB⊂平面PBC，所以PB⊥DE．‎ 又PB⊥EF，DE∩FE=E，所以PB⊥平面DEF．‎ 由DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，‎ 即四面体BDEF是一个鳖臑，其四个面的直角分别为∠DEB，∠DEF，∠EFB，∠DFB．‎ ‎（2）如图1，‎ 在面BPC内，延长BC与FE交于点G，则DG是平面DEF与平面ACBD的交线．‎ 由（Ⅰ）知，PB⊥平面DEF，所以PB⊥DG．‎ 又因为PD⊥底面ABCD，所以PD⊥DG．而PD∩PB=P，所以DG⊥平面PBD．‎ 所以DG⊥DF，DG⊥DB 故∠BDF是面DEF与面ABCD所成二面角的平面角，‎ 设PD=DC=1，BC=λ，有BD=，‎ 在Rt△PDB中，由DF⊥PB，得∠DGF=∠FDB=，‎ 则 tan=tan∠DPF===，解得．‎ 所以==‎ 故当面DEF与面ABCD所成二面角的大小为时，=．‎ ‎（解法2）‎ ‎（1）以D为原点，射线DA，DC，DP分别为x，y，z轴的正半轴，建立空间直角坐标系．设PD=DC=1，BC=λ，‎ 则D（0，0，0），P（0，0，1），B（λ，1，0），C（0，1，0），=（λ1，﹣1），点E是PC的中点，所以E（0，，），=（0，，），‎ 于是=0，即PB⊥DE．‎ 又已知EF⊥PB，而ED∩EF=E，所以PB⊥平面DEF．‎ 因=（0，1，﹣1），=0，则DE⊥PC，所以DE⊥平面PBC．‎ 由DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，‎ 即四面体BDEF是一个鳖臑，其四个面的直角分别为∠DEB，∠DEF，∠EFB，∠DFB．‎ ‎（2）由PD⊥底面ABCD，所以=（0，0，1）是平面ACDB的一个法向量；‎ 由（Ⅰ）知，PB⊥平面DEF，所以=（﹣λ，﹣1，1）是平面DEF的一个法向量．‎ 若面DEF与面ABCD所成二面角的大小为，‎ 则运用向量的数量积求解得出cos==，‎ 解得．所以所以==‎ 故当面DEF与面ABCD所成二面角的大小为时，=．‎ ‎【总结升华】空间向量最适合于解决这类立体几何中的探索性问题，它无需进行复杂繁难的作图、论证、推理，只需通过坐标运算进行判断。在解题过程上中，往往把“是否存在”问题，转化为“点的坐标是否有解，是否有规定范围的解”等，所以使问题的解决更简单、有效，在立体几何二轮复习中，我们要善于运用这一方法。‎ 举一反三：‎ ‎【变式】（2018 惠州模拟）如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=AD=1，CD=．‎ ‎（1）求证：平面PQB⊥平面PAD；‎ ‎（2）若二面角M﹣BQ﹣C为30°，设PM=tMC，试确定t的值．‎ ‎【解析】：（Ⅰ）证法一：∵AD∥BC，BC=AD，Q为AD的中点，‎ ‎∴四边形BCDQ为平行四边形，∴CD∥BQ．‎ ‎∵∠ADC=90°∴∠AQB=90°，即QB⊥AD．‎ 又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，‎ ‎∴BQ⊥平面PAD．‎ ‎∵BQ⊂平面PQB，∴平面PQB⊥平面PAD． ‎ 证法二：AD∥BC，BC=AD，Q为AD的中点，‎ ‎∴四边形BCDQ为平行四边形，∴CD∥BQ．‎ ‎∵∠ADC=90°∴∠AQB=90°．‎ ‎∵PA=PD，∴PQ⊥AD．‎ ‎∵PQ∩BQ=Q，∴AD⊥平面PBQ．‎ ‎∵AD⊂平面PAD，∴平面PQB⊥平面PAD． ‎ ‎（Ⅱ）∵PA=PD，Q为AD的中点，∴PQ⊥AD．‎ ‎∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，‎ ‎∴PQ⊥平面ABCD．‎ 如图，以Q为原点建立空间直角坐标系．‎ 则平面BQC的法向量为；‎ Q（0，0，0），，，．‎ 设M（x，y，z），则，，‎ ‎∵，‎ ‎∴，∴‎ 在平面MBQ中，，，‎ ‎∴平面MBQ法向量为 ‎∵二面角M﹣BQ﹣C为30°，‎ ‎∴，‎ ‎∴t=3‎