2020全国卷Ⅱ高考压轴卷数学（文）

2020全国卷Ⅱ高考压轴卷数学（文）

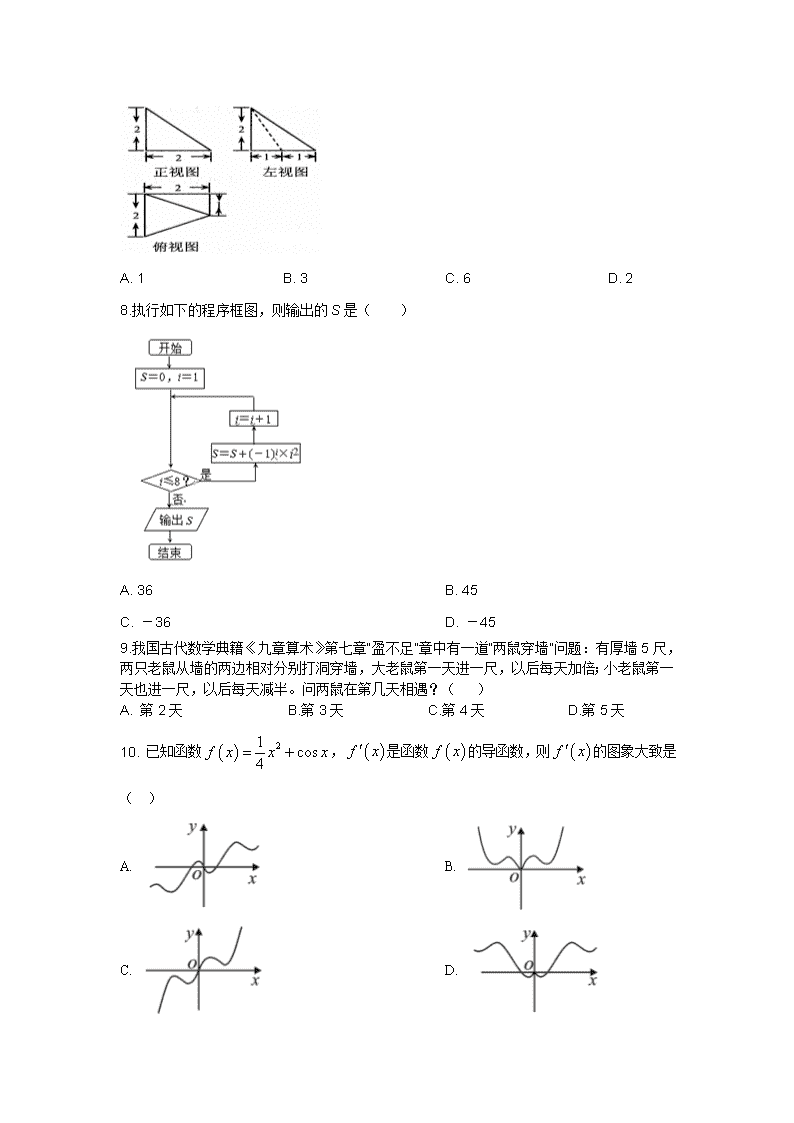
KS5U2020新课标2高考压轴卷数学（文）‎ 一、 选择题（本大题共12小题. 每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.已知集合A＝｛x｜0≤x≤3｝，B＝｛xR｜－2＜x＜2｝则A∩B=( )‎ A. {0,1} B. {1} C. [0,1] D. [0,2)‎ ‎2.已知复数z的共轭复数，则复数z的虚部是（ ）‎ A. B. C. D. ‎ ‎3.下列有关命题的说法正确的是（ ）‎ A. 命题“若，则”的否命题为：“若，则”‎ B. “”是“”必要不充分条件 C. 命题“，使”的否定是：“均有”‎ D. 命题“若，则”的逆否命题为真命题 ‎4.角的终边在直线上，则（ ）‎ A. B. 1 C. 3 D. －1‎ ‎5. 已知向量，，若向量与的夹角为，则实数m =（　　）‎ A. B. 1 C. －1 D. ‎ ‎6.设变量想x、y满足约束条件为则目标函数的最大值为( )‎ A. 0 B. -3 C. 18 D. 21‎ ‎7.一空间几何体的三视图如下图所示，则该几何体的体积为（ ） ‎ A. 1 B. 3 C. 6 D. 2‎ ‎8.执行如下的程序框图，则输出的S是（ ）‎ A. 36 B. 45‎ C. －36 D. －45‎ ‎9.我国古代数学典籍《九章算术》第七章“盈不足”章中有一道“两鼠穿墙”问题：有厚墙5尺，两只老鼠从墙的两边相对分别打洞穿墙，大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半。问两鼠在第几天相遇？（ ）‎ A. 第2天 B.第3天 C.第4天 D.第5天 ‎ ‎10. 已知函数，是函数的导函数，则的图象大致是（ ）‎ A. B. ‎ C. D. ‎ ‎11.双曲线C：的左、右焦点分别为F1、F2，P在双曲线C上，且是等腰三角形，其周长为22，则双曲线C的离心率为（　　）‎ A. B. C. D. ‎ ‎12.若定义在R上的函数满足且时，，则方程的根的个数是 A. 4 B. 5‎ C. 6 D. 7‎ 二、填空题（本大题共4小题.每小题5分，共20分）‎ ‎ ‎ ‎13.已知，且，则________．‎ ‎14.现有7名志愿者，其中只会俄语的有3人，既会俄语又会英语的有4人.从中选出4人担任“一带一路”峰会开幕式翻译工作，2人担任英语翻译，2人担任俄语翻译，共有_______种不同的选法。‎ ‎15.已知直线l：与圆交于A、B两点，过A、B分别作l的垂线与y轴交于C、D两点，若，则__________．‎ ‎16.已知三棱锥P－ABC，PA⊥平面ABC，AC⊥BC，PA＝2，AC＝BC＝1，则三棱锥P－ABC外接球的体积为__ .‎ 三、解答题（本大题共6小题，共70分.解答题应写出文字说明、证明过程或演算步骤）‎ ‎17. （本小题12分）‎ 已知数列{an}满足，．‎ ‎（1）证明：是等比数列；‎ ‎（2）求数列{an}的前n项和Sn．‎ ‎18. （本小题12分）‎ 如图所示，在三棱柱ABC - A1B1C1中，侧棱底面ABC，，D为AC的中点，.‎ ‎（1）求证：平面；‎ ‎（2）求AB1与BD所成角的余弦值．‎ ‎19. （本小题12分）‎ 某科研课题组通过一款手机APP软件，调查了某市1000名跑步爱好者平均每周的跑步量（简称“周跑量”），得到如下的频数分布表 周跑量（km/周）‎ 人数 ‎100‎ ‎120‎ ‎130‎ ‎180‎ ‎220‎ ‎150‎ ‎60‎ ‎30‎ ‎10‎ ‎（1）在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:‎ 注:请先用铅笔画，确定后再用黑色水笔描黑 ‎（2）根据以上图表数据计算得样本的平均数为28.5km，试求样本的中位数（保留一位小数），并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点 ‎（3）根据跑步爱好者的周跑量，将跑步爱好者分成以下三类，不同类别的跑者购买的装备的价格不一样，如下表: ‎ 周跑量 小于20公里 ‎20公里到40公里 不小于40公里 类别 休闲跑者 核心跑者 精英跑者 装备价格（单位：元）‎ ‎2500‎ ‎4000‎ ‎4500‎ 根据以上数据，估计该市每位跑步爱好者购买装备，平均需要花费多少元?‎ ‎20. （本小题12分）‎ 已知点，椭圆的离心率为是椭圆E的右焦点，直线AF的斜率为2，O为坐标原点．‎ ‎（1）求E的方程；‎ ‎（2）设过点且斜率为k的直线l与椭圆E交于不同的两M、N，且，求k的值.‎ ‎21. （本小题12分）‎ 已知函数 ‎（1）讨论f(x)的单调性；‎ ‎（2）设是f(x)的两个零点，证明：．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分，答题时用2B铅笔在答题卡上把所选的题号涂黑.‎ ‎22. （本小题10分）‎ 已知曲线C：（k为参数）和直线l：（t为参数）．‎ ‎（1）将曲线C的方程化为普通方程；‎ ‎（2）设直线l与曲线C交于A，B两点，且P（2，1）为弦AB的中点，求弦AB所在的直线方程．‎ ‎23. （本小题10分）‎ 设函数的最大值为m.‎ ‎（1）求m的值；‎ ‎（2）若正实数a，b满足，求的最小值.‎ KS5U2020新课标2高考压轴卷数学（文）Word版含解析 参考答案 ‎1. 【KS5U答案】A ‎【KS5U解析】‎ 可解出集合A，然后进行交集的运算即可．‎ ‎【详解】A＝{0，1，2，3}，B＝{x∈R|﹣2＜x＜2}；‎ ‎∴A∩B＝{0，1}．‎ 故选：A．‎ ‎2. 【KS5U答案】A ‎【KS5U解析】‎ ‎，则，则复数的虚部是.‎ 故选：A.‎ ‎3. 【KS5U答案】D ‎【KS5U解析】‎ ‎．命题“若，则”的否命题为：“若，则”，则错误．‎ ‎．由，解得或，则“”是“”的充分不必要条件，故错误．‎ ‎．命题“使得”的否定是：“均有”，故错误．‎ ‎．命题“若，则”为真命题，则根据逆否命题的等价性可知命题“若，则”的逆否命题为真命题，故正确．‎ 故选：D．‎ ‎4. 【KS5U答案】C ‎【KS5U解析】‎ 角的终边在直线上，，‎ 则，故选：C。‎ ‎5. 【KS5U答案】B ‎【KS5U解析】‎ 由题意得：，‎ ‎，‎ ‎，解得：‎ 本题正确选项：‎ ‎6. 【KS5U答案】C ‎【KS5U解析】‎ 画出可行域如下图所示，由图可知，目标函数在点处取得最大值，且最大值为.故选C.‎ ‎7. 【KS5U答案】D ‎【KS5U解析】‎ 由三视图可知，几何体是一个四棱锥，四棱锥的底面是一个直角梯形，‎ 直角梯形的上底是1，下底是2，垂直于底边的腰是2，‎ 一条侧棱与底面垂直，这条侧棱长是2.‎ 四棱锥的体积是.‎ 故选：D.‎ ‎8. 【KS5U答案】A ‎【KS5U解析】‎ 满足，执行第一次循环，，；‎ 成立，执行第二次循环，，；‎ 成立，执行第三次循环，，；‎ 成立，执行第四次循环，，；‎ 成立，执行第五次循环，，；‎ 成立，执行第六次循环，，；‎ 成立，执行第七次循环，，；‎ 成立，执行第八次循环，，；‎ 不成立，跳出循环体，输出的值为，故选：A.‎ ‎9. 【KS5U答案】B 第一天：大老鼠1+小老鼠1=2；‎ 第二天：大老鼠2+小老鼠1.5=3.5‎ 第三天：大老鼠4+小老鼠1.75=5.75相遇 ‎10. 【KS5U答案】A ‎【KS5U解析】由题意得：‎ ‎ 为奇函数，图象关于原点对称 可排除 又当时，，可排除 本题正确选项：‎ ‎11. 【KS5U答案】B ‎【KS5U解析】‎ 双曲线，可得a＝3，‎ 因为是等腰三角形，当时，‎ 由双曲线定义知|PF1|＝2a+|PF2|，‎ 在△F1PF2中，2c+2c+|PF2|＝22，‎ 即6c﹣2a＝22，‎ 即c，‎ 解得C的离心率e，‎ 当时，由双曲线定义知|PF1|＝2a+|PF2|=2a+2c，‎ 在△F1PF2中，2a+2c +2c+2c＝22，‎ 即6c＝22﹣2a=16，‎ 即c，‎ 解得C的离心率e<1（舍），‎ 故选：B．‎ ‎12. 【KS5U答案】A ‎【KS5U解析】‎ 因为函数满足，所以函数是周期为的周期函数.‎ 又时，，所以函数的图象如图所示.‎ 再作出的图象，易得两图象有个交点，所以方程有个零点．故应选A．‎ ‎13. 【KS5U答案】‎ ‎【KS5U解析】‎ 由得：‎ 解方程组：得：或 因为，所以所以不合题意，舍去 所以，所以，答案应填：.‎ ‎14. 【KS5U答案】60‎ ‎【KS5U解析】‎ 因为英语翻译只能从多面手中选，所以有 ‎（1）当选出的多面手2人从事英语翻译，没人从事俄语翻译，所以有种选法；‎ ‎（2）当选出的多面手2人从事英语翻译，1人从事俄语翻译，所以有种选法；‎ ‎（3）当选出的多面手2人从事英语翻译，2人从事俄语翻译，所以有种选法；‎ 共有18+36+6=60种选法。‎ ‎15. 【KS5U答案】4‎ ‎【KS5U解析】‎ 因为，且圆的半径为，所以圆心到直线的距离为，则由，解得，代入直线的方程，得，所以直线的倾斜角为30°，由平面几何知识知在梯形中，．‎ 故答案为4‎ ‎16. 【KS5U答案】‎ ‎【KS5U解析】如图所示,取PB的中点O，∵PA⊥平面ABC，∴PA⊥AB，PA⊥BC，又BC⊥AC，PA∩AC＝A，∴BC⊥平面PAC，∴BC⊥PC.∴OA＝PB，OC＝PB，∴OA＝OB＝OC＝OP，故O为外接球的球心．又PA＝2，AC＝BC＝1，∴AB＝，PB＝，∴外接球的半径R＝.‎ ‎∴V球＝πR3＝×()3＝,故填.‎ 三、解答题（本大题共6道题，其中17题10分，其余每题12分，共计70分，请将准确的答案写在答题卡相应的区域内.）‎ ‎17. 【KS5U答案】（1）见解析；（2）．‎ ‎【KS5U解析】‎ ‎（1）由题意，数列满足，所以 又因为，所以，即，‎ 所以是以2为首项，2为公比的等比数列．‎ ‎（2）由（1），根据等比数列的通项公式，可得，即，‎ 所以 ‎ ‎，‎ 即．‎ ‎18. 【KS5U答案】（1）证明见解析；（2） .‎ ‎【KS5U解析】‎ ‎ (1)证明：如图，连接，设与相交于点O，连接OD. ‎ ‎∵四边形是平行四边形．‎ ‎∴点O为的中点． ‎ ‎∵D为AC的中点，‎ ‎∴OD为的中位线，‎ ‎ ‎ 平面，平面， 平面 .‎ ‎（2）由（1）可知，为与所成的角或其补角 ‎ 在中，D为AC的中点，则 同理可得， ‎ 在中， ‎ 与BD所成角的余弦值为 .‎ ‎19. 【KS5U答案】(1)见解析；(2) 中位数为29.2，分布特点见解析； (3)3720元 ‎【KS5U解析】‎ ‎（1）补全该市1000名跑步爱好者周跑量的频率分布直方图，如下：‎ ‎（2）中位数的估计值：‎ 由，‎ 所以中位数位于区间中，‎ 设中位数为，则，‎ 解得，因为，‎ 所以估计该市跑步爱好者多数人的周跑量多于样本的平均数．‎ ‎（3）依题意可知，休闲跑者共有人，‎ 核心跑者人，‎ 精英跑者人，‎ 所以该市每位跑步爱好者购买装备，平均需要元．‎ ‎20. 【KS5U答案】（1）；（2）或.‎ ‎【KS5U解析】‎ 解：（1）由离心率e，则ac，‎ 直线AF的斜率k2，则c＝1，a，‎ b2＝a2﹣c2＝1，‎ ‎∴椭圆E的方程为；‎ ‎（2）设直线l：y＝kx﹣，设M（x1，y1），N（x2，y2），‎ 则，整理得：（1+2k2）x2﹣kx+4＝0，‎ ‎△＝（﹣k）2﹣4×4×（1+2k2）＞0，即k2，‎ ‎∴x1+x2，x1x2，‎ ‎∴，‎ 即,‎ 解得：或（舍去）‎ ‎∴k＝±，‎ ‎21. 【KS5U答案】（1）见解析（2）见解析 ‎【KS5U解析】‎ ‎（1），‎ 当时，，则在上单调递增．‎ 当时，令，得，则的单调递增区间为，‎ 令，得，则的单调递减区间为．‎ ‎（2）证明：由得，设，则．‎ 由，得；由，得．‎ 故的最小值．‎ 当时，，当时，，‎ 不妨设，则，‎ 等价于，且上单调递增，‎ 要证：，只需证，‎ ‎，‎ 只需证，即，‎ 即证；‎ 设，‎ 则，‎ 令，则，，‎ 在上单调递减，即在上单调递减，‎ ‎，在上单调递增，‎ ‎，‎ 从而得证．‎ ‎22. 【KS5U答案】（1），（2）x+2y﹣4＝0．‎ ‎【KS5U解析】（1）由，得，即，又，两式相除得，‎ 代入，得，整理得，即为C的普通方程．‎ ‎（2）将代入，‎ 整理得（4sin2θ+cos2θ）t2+（4cosθ+8sinθ）t﹣8＝0．‎ 由P为AB的中点，则．‎ ‎∴cosθ+2sinθ＝0，即，故，即，‎ 所以所求的直线方程为x+2y﹣4＝0．‎ ‎23. 【KS5U答案】(1) m＝1 (2)‎ ‎【KS5U解析】（1）f(x)＝|x＋1|－|x|＝ ‎ 由f(x)的单调性可知，当x≥1时，f(x)有最大值1．‎ 所以m＝1．‎ ‎（2）由（1）可知，a＋b＝1，‎ ‎＋＝ (＋)[(b＋1)＋(a＋1)]‎ ‎＝ [a2＋b2＋＋]‎ ‎≥ (a2＋b2＋2)‎ ‎＝ (a＋b)2‎ ‎＝．‎ 当且仅当a＝b＝时取等号．‎ 即＋的最小值为．‎