- 2021-06-16 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
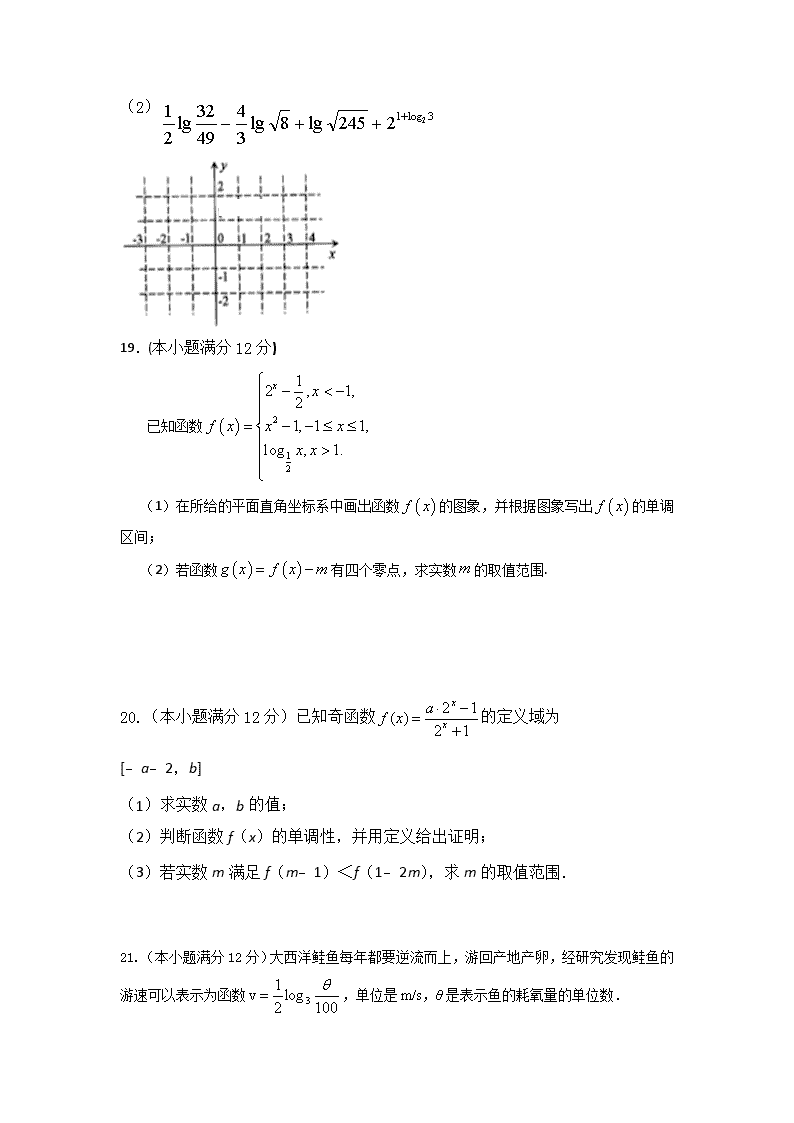
2018-2019学年河南省安阳市第二中高一上学期期中考试试卷 数学 (word版)
安阳市第二中学2018-2019学年第一学期期中考试 高一数学试题卷 一、选择题(每小题5分,共60分) 1.全集,集合A=集合B=则=( ) A. B. C. D. 2.函数的定义域为( ) A. B. C. D. 3.设,,,则的大小关系为( ) A. B. C. D. 4、下列函数中,既是偶函数又在上单调递增的是( ) A. B. C. D. 5、在下列区间中函数的零点所在的区间为( ) A. B. C. D. 6.若则等于( ) A.1 B.3 C.15 D.30 7. 下列三种叙述, ①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台; ②两个面平行且相似,其余各面都是梯形的多面体是棱台; ③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台. 其中正确的有 ( ) A.0个 B.1个 C.2个 D.3个 8.已知函数则的值等于( ) A.1 B.2 C.3 D.9 9.已知函数,则( ) A.4 B.±2 C.﹣2 D.2 10.若函数在是单调递减的,则实数的取值范围是( ) A. B. C. D. 11、已知是定义在上的偶函数,当时,,则不等式的解集为( ) A. B. C . D . 12.已知函数若关于的方程有四个不同的实数解,且则的取值范围是( ) A. B. C. D. 二、填空题(每题5分,共20分) 13.已知集合A=,集合满足= ,则集合B有 个. 14.函数的图像恒过定点,且点在幂函数的图像上,则 . 15.已知,则_________ . 16.已知满足对任意成立,那么的取值范围是________. 三、解答题 17.(本小题满分10分)已知集合, (1)设全集,求C; (2)已知集合,若,求实数的取值范围. 18. (本小题满分12分)求下列各式的值: (1); (2) 19.(本小题满分12分) 已知函数 (1)在所给的平面直角坐标系中画出函数的图象,并根据图象写出的单调区间; (2)若函数有四个零点,求实数的取值范围. 20.(本小题满分12分)已知奇函数的定义域为 [﹣a﹣2,b] (1)求实数a,b的值; (2)判断函数f(x)的单调性,并用定义给出证明; (3)若实数m满足f(m﹣1)<f(1﹣2m),求m的取值范围. 21.(本小题满分12分)大西洋鲑鱼每年都要逆流而上,游回产地产卵,经研究发现鲑鱼的游速可以表示为函数,单位是m/s,θ是表示鱼的耗氧量的单位数. (1)当一条鲑鱼的耗氧量是900个单位时,它的游速是多少? (2)计算一条鱼静止时耗氧量的单位数。 (3)某条鲑鱼想把游速提高1 m/s,那么它的耗氧量的单位数是原来的多少倍? 22.(本小题满分12分)已知函数, (Ⅰ) 求函数的定义域,判断并证明函数的奇偶性; (Ⅱ) 是否存在这样的实数,使对一切恒成立,若存在,试求出的取值集合;若不存在,请说明理由. 高一数学答案 一、 选择题(每小题5分) 1-5BCBAB 6-10CAADB 11-12DD 二、 填空题(每小题5分) 13. 4 14. 9 15. 2 16. 三解答题 17.(10分)解:(1) .............................2分 ∴ C ..........................................5分 由题意可知 且∅ .........10分(无等号扣2分) 18.(12分)解:(1)原式=;......... ......... ........ .. .... 6分 (2)原式= ==......... ........... .......12分 19. (12分)解:(1)函数的图象如图示,……………………………………….6分 由图象可得函数的单调递增区间为和,单调递减区间为和;…………………………………………………………………………………….9分 (2)由函数的图象可知,当且仅当时,函数有四个零点,∴实数的取值范围为…………………………………………………………………………12分 20. (12分)解(1)∵f(x)是奇函数,故f(0)=0,即a﹣1=0,解得:a=1,故﹣a﹣2=﹣3, 定义域为[﹣a﹣2,b],关于原点对称,故b=3;........ ............... ........4分 (2)函数f(x)在[﹣3,3]递增, 证明如下:设x1,x2是[﹣3,3]上的任意2个值,且x1<x2, 则f(x1)﹣f(x2)=﹣=, ∵﹣3≤x1<x2≤3,∴﹣<0,又+1>0,+1>0, ∴f(x1)﹣f(x2)<0,即f(x1)<f(x2), ∴f(x)在[﹣3,3]递增;........ ........ ......... ........ ........ ........ 8分 (3)由(1)得f(x)在[﹣3,3]递增, ∴f(m﹣1)<f(1﹣2m)等价于: ,解得:﹣1≤m<, 故不等式的解集是[﹣1,)......... .......... ........ ....... …………….12分 21. (12分)(1)由v=log3可知, 当θ=900时,v=log3=log39=1(m/s). 所以当一条鲑鱼的耗氧量是900个单位时,它的游速是1 m/s. ………………….. 4分 (2)令V=0,则 …………………………………………………………. 8分 (3)由v2-v1=1,即log3-log3=1,得=9. 所以耗氧量的单位数为原来的9倍.………………………………………………………12分 22. (12分)解:(Ⅰ)由…………………………………………3分 ∴是奇函数.--------6分 (Ⅱ) 假设存在满足题设条件的实数,则 令,则在上单调递减,又在上单调递增,于是函数在上单调递减. --------8分 于是,由(Ⅰ) 及已知不等式等价于 . (1) 由题意,不等式(1)对一切恒成立,即不等式组对一切恒成立. --------11分 所以即.故不存在. --------12分查看更多