高中数学选修2-3教学课件第一讲不等式和绝对值不等式（三）

高中数学选修2-3教学课件第一讲不等式和绝对值不等式（三）

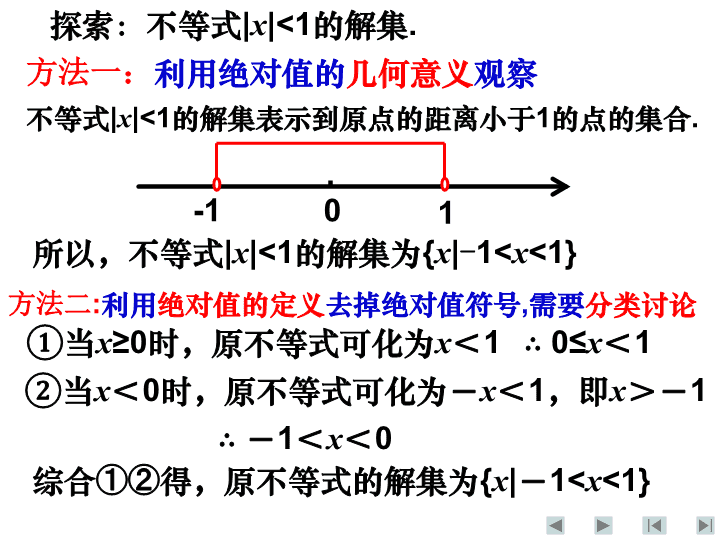
尝试练习一 练习二 问题引入 解法公式 本课小结 补充练习 方法一 : 利用绝对值的几何意义观察； 方法二 : 利用绝对值的定义去掉绝对值符号 , 需要分类讨论 ; 方法三 : 两边同时平方去掉绝对值符号 ; 方法四 : 利用函数图象观察 . 这也是解其他含绝对值不等式的四种常用思路 . 主要方法有 : 0 -1 不等式 | x |<1 的解集表示到原点的距离小于 1 的点的集合 . 1 所以，不等式 | x |<1 的解集为 { x | - 1< x <1} 探索：不等式 | x |<1 的解集 . 方法一： 利用绝对值的 几何意义 观察 ① 当 x ≥0 时，原不等式可化为 x ＜ 1 ② 当 x ＜ 0 时，原不等式可化为－ x ＜ 1 ，即 x ＞－ 1 ∴ 0≤ x ＜ 1 ∴ － 1 ＜ x ＜ 0 综合①②得，原不等式的解集为 { x | － 1< x <1} 方法二 : 利用 绝对值的定义 去掉绝对值符号 , 需要 分类讨论 探索：不等式 | x |<1 的解集。 对原不等式两边平方得 x 2 <1 即 x 2 － 1<0 即 ( x +1)( x － 1)<0 即－ 1< x <1 所以，不等式 | x |<1 的解集为 { x | - 1< x <1} 方法三： 两边同时 平方去掉绝对值 符号 . 从函数观点看，不等式 | x |<1 的解集表示函数 y =| x | 的图象位于函数 y =1 的图象下方的部分对应的 x 的取值范围 . o x y 1 1 － 1 y =1 所以，不等式 | x |<1 的解集为 { x | - 1< x <1} 方法四： 利用 函数图象 观察 一般地，可得解集规律 : 形如 | x |< a 和 | x |> a ( a >0 ) 的含绝对值的不等式的解集 : ① 不等式 | x |< a 的解集为 { x | - a a 的解集为 { x | x < - a 或 x > a } 0 - a a 0 - a a 解法公式拓广 挑战题 试解下列不等式： 课堂练习一： 1 答案 2 答案 课堂练习二 ( 挑战 ) ： 2. 试解不等式 | x -1|+| x +2|≥5 解绝对值不等式关键是去绝对值符号 , 你有什么方法解决这个问题 ? 还有没有其他方法 ? 2. 试解不等式 | x -1|+| x +2|≥5 方法一： 利用绝对值的几何意义，体现了数形结合的思想． -2 1 2 -3 解 :| x -1|+| x +2|=5 的解为 x =-3 或 x =2 所以原 不等式 的解为 方法小结 2. 解不等式 | x -1|+| x +2|≥5 解：１ ０ 当 x> 1 时，原不等式同解于 x ≥ 2 x <-2 -( x -1)-( x +2) ≥ 5 ( x -1)+( x +2) ≥ 5 x >1 -( x -1)+( x +2) ≥ 5 x ≤ -3 综合上述知不等式的解集为 3 ０ 当 x <-2 时，原不等式同解于 2 ０ 当 -2 ≤ x ≤ 1 时，原不等式同解于 方法二： 利用 | x -1|=0 ， | x +2|=0 的零点，将数轴分为三个区间，然后在这三个区间上将原不等式分别化为不含绝对值符号的不等式求解．体现了分类讨论的思想． 2. 解不等式 | x -1|+| x +2|≥5 解 原不等式化为 | x -1|+| x +2|-5 ≥0 ( x -1)+( x +2)-5 ( x >1) -( x -1)+( x +2)-5 (-2≤ x ≤1) -( x -1)-( x +2)-5 ( x <-2) f ( x )= 2 x -4 ( x >1) -2 (-2≤ x ≤1) -2 x -6 ( x <-2) 令 f ( x )=| x -1|+| x +2|-5 , 则 -3 1 2 -2 -2 x y 由图象知不等式的解集为 f ( x )= 方法三： 通过构造函数，利用函数的图象，体现了函数与方程的思想． 方法小结 3. 不等式 有解的条件是 ( ) 1. 解不等式 |2 x -4|-|3 x +9|<1 B 1. 解不等式 |2 x -4|-|3 x +9|<1 解：１ ０ 当 x >2 时，原不等式同解于 x >2 3 ０ 当 x <-3 时，原不等式同解于 2 ０ 当 -3 ≤ x ≤ 2 时，原不等式同解于 x <-3 -(2 x -4)+(3 x +9)<1 (2 x -4)-(3 x +9)<1 x >2 -(2 x -4)-(3 x +9)<1 x <-13 综合上述知不等式的解集为