新教材数学北师大版（2019）必修第二册课件：1-8 三角函数的简单应用 课件（58张）

新教材数学北师大版（2019）必修第二册课件：1-8 三角函数的简单应用 课件（58张）

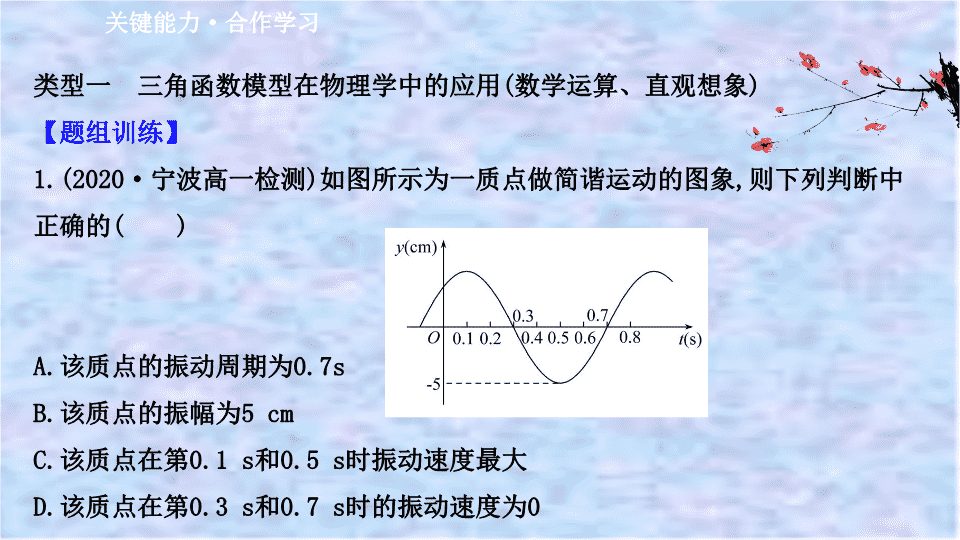
§8　三角函数的简单应用 类型一　三角函数模型在物理学中的应用(数学运算、直观想象) 【题组训练】 1.(2020·宁波高一检测)如图所示为一质点做简谐运动的图象,则下列判断中 正确的(　　) A.该质点的振动周期为0.7s B.该质点的振幅为5 cm C.该质点在第0.1 s和0.5 s时振动速度最大 D.该质点在第0.3 s和0.7 s时的振动速度为0 关键能力·合作学习 2.(2020·潍坊高一检测)如图所示,单摆从某点开始来回摆动,离开平衡位置O的 弧长s(cm)与时间t(s)的函数关系式为s=6sin ,那么单摆来回摆动一次 所需的时间为 (　　) 　　　　　　　　　　　　　　　　　　 A.2π s B.π s C.0.5 s D.1 s (2 t )6   3.交流电的电压E(单位:V)与时间t(单位:s)的关系可用E=220 sin 来表示,求: (1)开始时电压; (2)电压值重复出现一次的时间间隔; (3)电压的最大值和第一次获得最大值的时间. (100 t )6  3 【解析】 1.选B.由图象可知周期是0.8 s,A错误,振幅为5 cm,B正确;质点在第0.1 s和 0.5 s时振动速度为0,C错误,质点在第0.3 s和0.7 s时的振动速度不为0,D错误. 2.选D.单摆来回摆动一次,即完成一个周期, 因为s=6sin 的最小正周期T= =1, 所以单摆来回摆动一次所需的时间为1 s. 3.(1)当t=0时E=110 (V),即开始时的电压为110 V. (2)T= = (s),即时间间隔为0.02 s. (3)电压的最大值为220 V,当100πt+ = ,即t= s时第一次取得最大值. (2 t )6   2 2   2 100   3 1 50 3 3 6  2  1 300 【解题策略】 三角函数在物理中的应用 在物理学中,物体做简谐运动时可用正弦型函数y=Asin(ωx+φ)表示物体振动 的位移y随时间x的变化规律,A为振幅,表示物体离开平衡位置的最大距离, T= 为周期,表示物体往复振动一次所需的时间,f= 为频率,表示物体在单位 时间内往复振动的次数. 2  1 T 【补偿训练】 已知弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移s(cm)随时间 t(s)的变化规律为s=4sin ,t∈[0,+∞).用“五点法”作出这个函数的 简图,并回答下列问题. (1)小球在开始振动(t=0)时的位移是多少? (2)小球上升到最高点和下降到最低点时的位移分别是多少? (3)经过多长时间小球往复振动一次? (2t 3 ＋ ） 【解析】列表: 描点、连线,图象如图所示. 　　　 (1)将t=0代入s=4sin , 得s=4sin =2 , 所以小球开始振动时的位移是2 cm. (2)小球上升到最高点和下降到最低点时的位移分别是4 cm和-4 cm. (3)因为振动的周期是π,所以小球往复振动一次所用的时间是π s. (2t 3 ＋ ） 3 3 3  类型二　三角函数模型的实际应用(数学建模、数学运算) 【典例】已知某海滨浴场的海浪高度y(米)是时间t(时)的函数,其中0≤t≤24, 记y=f(t),下表是某日各时的浪高数据: t 0 3 6 9 12 15 18 21 24 y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5 经长期观测,y=f(t)的图象可近似地看成是函数y=Acos ωt+b的图象. (1)根据以上数据,求其最小正周期,振幅及函数解析式; (2)根据规定,当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判 断一天内的8:00到20:00之间有多少时间可供冲浪者进行活动? 【思路导引】(1)根据y的最大值和最小值求A,b,周期及ω. (2)解不等式y>1,确定有多少时间可供冲浪者活动. 【解析】(1)由表中数据可知,T=12,所以ω= .又t=0时,y=1.5,所以A+b=1.5; t=3时,y=1.0,得b=1.0,所以振幅为 ,函数解析式为y= cos t+1(0≤t≤24). (2)因为y>1时才对冲浪爱好者开放, 所以y= cos t+1>1,cos t>0,2kπ- < t<2kπ+ , 即12k-31.25,得cos t> , 2kπ- < t<2kπ+ ,k∈Z, 即12k-28, 所以sin > , 所以 +2kπ< x- < +2kπ,k∈Z, 可得 +8k0,ω>0,0≤φ< )的振 幅为1,周期为2π,初相为0,知声波曲线:y=sin x,通过听感主动降噪芯片生成 相等的反向波曲线为y=-sin x. 2  3.(2020·枣庄高一检测)如图,质点P在半径为2的圆周上逆时针运动,其初始 位置为P0( ,- ),角速度为1,那么点P到x轴的距离d关于时间t的函数图象 大致为 2 2 【解析】选C.通过分析可知当t=0时,点P到x轴距离d为 ,于是可以排除选项 A,D;再根据当t= π时,点P在x轴上,此时点P到x轴距离d为0,排除选项B. 2 1 4 4.(2020·重庆高一检测)重庆被誉为“桥都”,数十座各式各样的大桥横跨长江、嘉 陵江两岸,其中朝天门长江大桥是世界第一大拱桥,其主体造型为:桥拱部分(开 口向下的抛物线)与主桁(图中粗线)部分(可视为余弦函数一个周期的图象)相结 合.已知拱桥部分长552 m,两端引桥各有190 m,主桁最高处距离桥面89.5 m,则将 下列函数等比放大后,与主桁形状最相似的是 A.y=0.45cos x B.y=4.5cos x C.y=0.9cos x D.y=9cos x 2 3 3 2 3 2 2 3 【解析】选A.设主桁(图中粗线)部分对应的余弦函数为f（x）=Acos ωx, 可得函数的周期为T=552+190×2=932, 即ω= ,又由2A=89.5,解得A= , 所以函数的解析式为f（x）= cos x, 按1∶100的比例等比变换可得f（x）= cos x 对比选项,可得与函数y=0.45cos x相似. 2 932 466   89.5 2 89.5 2 100 466 89.5 2002 3 466  5.如图,某地一天从6时到14时的温度变化曲线近似满足函数 y=Asin(ωx+φ)+b(A>0,ω>0),则8时的温度大约为________℃(精确到1℃). 【解析】由图象可得b=20,A=10, T=14-6=8, 所以T=16= ⇒ω= ,y=10sin +20,因为最低点坐标为(6,10), 所以10sin +20=10,得sin =-1, 于是 +φ= π+2kπ(k∈Z),所以φ= π+2kπ(k∈Z), 取φ= π,所以y=10sin +20. 当x=8时y=10sin +20=20-5 ≈13. 答案:13 1 2 2  8  ( x )8    3( )4    3 4  3 2 3 4 3 4 3( x )8 4    3( )4    2 ( 6 )8     6.(2020·牡丹江高一检测)如图,游乐场的摩天轮匀速旋转,每转一周需要 12 min,其中心O离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与 地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当 你第六次距离地面65米时,用了________分钟.  【解析】设时间为t,t>0,根据题意: 40sin +45=65,故sin = . 故 t- = +2kπ或 t- = +2kπ, 故t=12k+4或t=12k+8,k∈Z. 故t1=4,t2=8,t3=16,t4=20,t5=28,t6=32. 答案:32 ( t )6 2   ( t )6 2   1 2 6  6  6  5 6  2  2  【能力进阶—水平二】(30分钟　60分) 一、单选题(每小题5分,共20分) 1.在两个弹簧上各有一个质量分别为M1和M2的小球做上下自由振动.已知它们 在时间t(s)离开平衡位置的位移s1(cm)和s2(cm)分别由s1=5sin , s2=10cos 2t确定,则当t= s时,s1与s2的大小关系是 (　　) A.s1>s2 B.s10,ω>0,φ∈[0,2π)),由题意可知A=60, B=135-60=75,T= =30,所以ω= ,即f(t)=60sin +75. 又因为f(0)=135-120=15,解得sin φ=-1,故φ= , 所以f(t)=60sin +75=-60cos t+75, 所以f(10)=-60×cos +75=105. 2  15  ( t )15    3 2  3( t )15 2   15  2 3  二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错 的得0分) 5.如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数 y=Asin(ωx+φ)+B(0<φ<π),则下列说法正确的是 (　　) A.该函数的周期是16 B.该函数图象的一条对称轴是直线x=14 C.该函数的解析式是y=10sin +20(6≤x≤14) D.这一天的函数关系式也适用于第二天 3( x )8 4   【解析】选AB.由题意以及函数的图象可知,A+B=30,-A+B=10,所以A=10,B=20. 因为 =14-6=8,所以T=16,A正确;因为T= ,所以ω= , 所以y=10sin +20,因为图象经过点(14,30), 所以30=10sin +20,所以sin =1,所以φ可以取 , 所以y=10sin +20(0≤x≤24),B正确,C错误;这一天的函效关系式只适 用于当天,第二天这个关系式不一定适用,所以D错误. T 2 2  8  ( x )8    ( 14 )8     ( 14 )8     3 4  3( x )8 4   6.(2020·广州高一检测)如图,一个水轮的半径为6 m,水轮轴心O距离水面的高 度为3 m,已知水轮按逆时针匀速转动,每分钟转动5圈,当水轮上点P从水中浮 现时的起始(图中点P0)开始计时,记f(t)为点P距离水面的高度关于时间t(s)的 函数,则下列结论正确的是 (　　) A.f(3)=9 B.f(1)=f(7) C.若f(t)≥6,则t∈[2+12k,5+12k](k∈N) D.不论t为何值,f(t)+f(t+4)+f(t+8)是定值 【解析】选BD.如图,以水轮所在面为坐标平面,以水轮的轴心O为坐标原点, x轴和y轴分别平行和垂直于水面建立平面直角坐标系,依题意得OP在t(s)内所 转过的角度为t,则∠POx= t- .则点P的纵坐标为y=6sin ,点P距离水 面的高度关于时间t(s)的函数f（t）=6sin +3; f（3）=6sin +3=3 +3,选项A错误; f（1）=6sin +3=3, f（7）=6sin +3=3,f（1）=f（7）,选项B正确; 6  6  ( t )6 6   ( t )6 6   ( )6 6   ( )2 6   7( )6 6   3 由f（t）≥6得sin ≥ , 解得t∈[2+12k,6+12k]k∈N,选项C错误; 由f(t)+f（t+4）+f(t+8)=6sin +3+6sin +3 +6sin +3,展开整理得f(t)+f（t+4）+f(t+8)= 9为定值,选项D正确. ( t )6 6   1 2 ( t )6 6   3( t )6 6   7( t )6 6   三、填空题(每小题5分,共10分) 7.(2020·福州高一检测)我们听到的美妙弦乐不是一个音在响,而是许多个纯 音的合成,称为复合音.复合音的响度是各个纯音响度之和.琴弦在全段振动, 产生频率为f的纯音的同时,其二分之一部分也在振动,振幅为全段的 ,频率 为全段的2倍;其三分之一部分也在振动,振幅为全段的 ,频率为全段的3倍; 其四分之一部分也在振动,振幅为全段的 ,频率为全段的4倍;之后部分均忽 略不计.已知全段纯音响度的数学模型是函数y1=sin t(t为时间,y1为响度),则 复合音响度数学模型的最小正周期是________.  1 3 1 2 1 4 【解析】因为产生频率为f的纯音的同时,其二分之一部分也在振动,振幅为全 段的 ,频率为全段的2倍;其三分之一部分也在振动,振幅为全段的 ,频率为 全段的3倍;其四分之一部分也在振动,振幅为全段的 ,频率为全段的4倍;由 全段纯音响度的数学模型是函数y1=sin t(t为时间,y1为响度),可得复合音响 度数学模型为y= sin 2t+ sin 3t+ sin 4t, 1 2 1 3 1 4 1 2 1 3 1 4 因为y= sin 2t的周期为 =π, y= sin 3t的周期为 ,y= sin 4t的周期为 = 且π, , 的最小公倍 数为2π, 所以y= sin 2t+ sin 3t+ sin 4t的周期为2π. 答案:2π 1 4 1 2 1 3 2 2  2 3  2 4  2  2 3  2  1 2 1 3 1 4 8.(2020·南昌高一检测)某时钟的秒针端点A到中心点O的距离为5 cm,秒针均 匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合,将A,B两点的距离 d(cm)表示成t(s)的函数,则d=______,其中t∈[0,60].  【解析】因为∠AOB= ×2π= , 所以根据直角三角形的边长求法得到d=2×5×sin ∠AOB=10sin . 答案:10sin t 60 t 30  1 2 t 60  t 60  四、解答题(每小题10分,共20分) 9.某实验室一天的温度(单位℃)随时间t(单位:h)的变化近似满足函数关系 式:f(t)=12-2cos ,t∈[0,24). (1)求该实验室一天当中上午10时的温度; (2)若某实验需要在不低于13 ℃的条件下才可以做,那么该实验应该在一天当 中的哪个时间段进行? ( t )12 6   【解析】(1)因为f(t)=12-2cos ,t∈[0,24), 所以f(10)=12-2cos =12-2cos =13(℃), 所以该实验室一天当中上午10时的温度为13 ℃. (2)令f(t)=12-2cos ≥13,即cos ≤- , 所以2kπ+ ≤ ≤2kπ+ ,k∈Z, 所以24k+10≤t≤24k+18,k∈Z. 因为0≤t<24,所以10≤t≤18,故该实验应该在一天中t∈[10,18]这个时间段 进行.即10时至18时进行. ( t )12 6   5( )6 6   2 3  ( t )12 6   ( t )12 6   1 2 2 3  t12 6   4 3  10.建设生态文明,是关系人民福祉,关乎民族未来的长远大计.某市通宵营业 的大型商场,为响应节能减排的号召,在气温超过28 ℃时才开放中央空调降温, 否则关闭中央空调.如图是该市夏季一天的气温(单位:℃)随时间(0≤t≤24, 单位:小时)的大致变化曲线,若该曲线近似的满足函数y=Asin(ωt+φ) +b 关系.(A 0, 0, )      (1)求函数y=f(x)的表达式; (2)请根据(1)的结论,判断该商场的中央空调应在本天内何时开启?何时关闭? 【解析】(1)由题图知,T=2(14-2)=24,所以 =24,得ω= . 由题图知b= =24,A= =8, 所以f(t)=8sin +24. 将点(2,16)代入函数解析式得24+8sin =16, 得 +φ=2kπ- ,(k∈Z), 即φ=2kπ- π(k∈Z),又因为 <π,得φ=- π. 所以f(t)=24+8sin . 2  12  16 32 2  32 16 2  ( t )12    ( 2 )12     6  2  2 3  2 3 2( t )(0 t 24)12 3      (2)依题意令24+8sin >28, 可得sin > , 所以2kπ+ < t- π<2kπ+ π,(k∈Z). 解得24k+10

查看更多