山东省济南市2020届高三5月二模数学试题

山东省济南市2020届高三5月二模数学试题

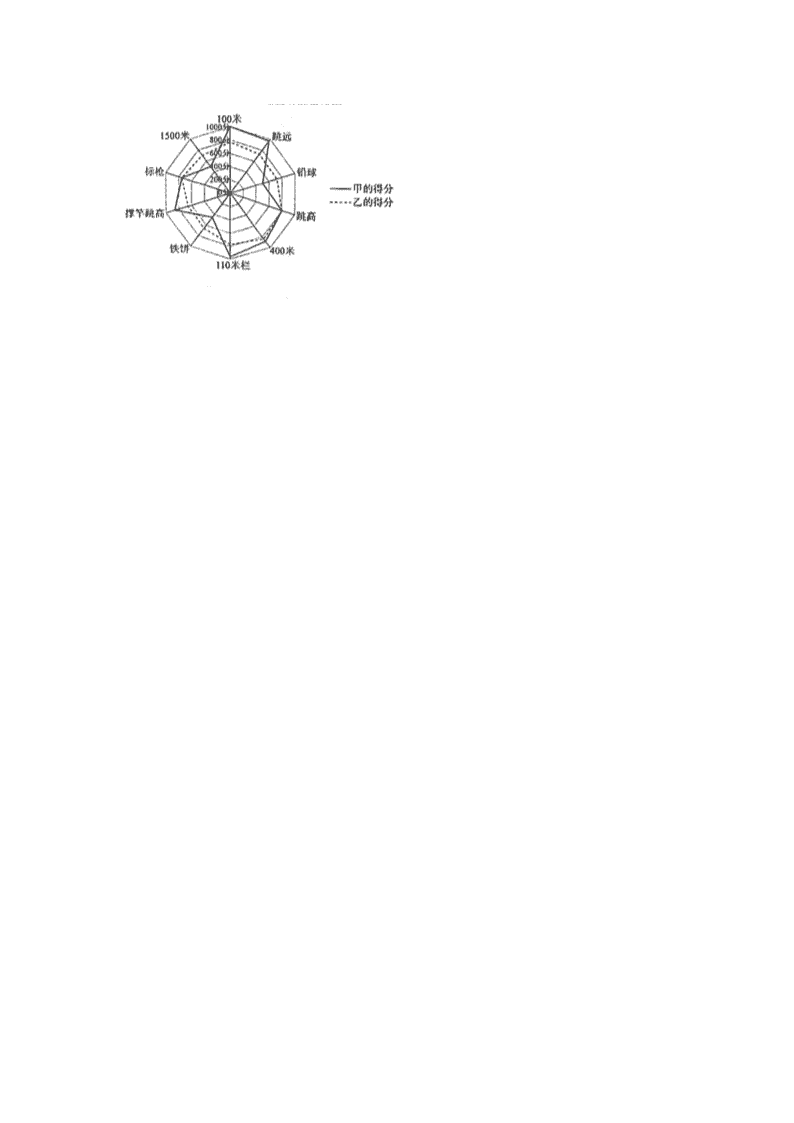
绝密★启用并使用完毕前 ‎ 高考模拟考试 ‎ 数学试题 本试卷共6页,22小题,满分150分考试用时120分钟。‎ 注意事项:‎ ‎1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上 ‎2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上写在本试卷上无效。‎ ‎3.考试结束后将本试卷和答题卡一并交回。‎ 参考公式:锥体的体积公式（其中S为锥体的底面积h为锥体的高）‎ 一、单项选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一 项是符合题目要求的 ‎1.已知α为第四象限角,则，则sinα=‎ ‎2.已知x,集合则xy=‎ A.-1 ‎ ‎3.已知抛物线的焦点为F,点P在抛物线上且横坐标为4,则|PF|=‎ A.2 B‎.3C.5 D.6‎ ‎4.十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目,按照国际田径联合会制定的田径运动全能评分表计分,然后将各个单项的得分相加,总分多者为优胜.下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图.‎ 绝密★启用并使用完毕前 ‎ 高考模拟考试 ‎ 数学试题 本试卷共6页,22小题,满分150分考试用时120分钟。‎ 注意事项:‎ ‎1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上 ‎2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上写在本试卷上无效。‎ ‎3.考试结束后将本试卷和答题卡一并交回。‎ 参考公式:锥体的体积公式（其中S为锥体的底面积h为锥体的高）‎ 一、单项选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一 项是符合题目要求的 ‎1.已知α为第四象限角,则，则sinα=‎ ‎2.已知x,集合则xy=‎ A.-1 ‎ ‎3.已知抛物线的焦点为F,点P在抛物线上且横坐标为4,则|PF|=‎ A.2 B‎.3C.5 D.6‎ ‎4.十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目,按照国际田径联合会制定的田径运动全能评分表计分,然后将各个单项的得分相加,总分多者为优胜.下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图.‎ 绝密★启用并使用完毕前 ‎ 高考模拟考试 ‎ 数学试题 本试卷共6页,22小题,满分150分考试用时120分钟。‎ 注意事项:‎ ‎1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上 ‎2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上写在本试卷上无效。‎ ‎3.考试结束后将本试卷和答题卡一并交回。‎ 参考公式:锥体的体积公式（其中S为锥体的底面积h为锥体的高）‎ 一、单项选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一 项是符合题目要求的 ‎1.已知α为第四象限角,则，则sinα=‎ ‎2.已知x,集合则xy=‎ A.-1 ‎ ‎3.已知抛物线的焦点为F,点P在抛物线上且横坐标为4,则|PF|=‎ A.2 B‎.3C.5 D.6‎ ‎4.十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目,按照国际田径联合会制定的田径运动全能评分表计分,然后将各个单项的得分相加,总分多者为优胜.下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图.‎ 下列说法错误的是 A.在‎100米项目中,甲的得分比乙高 B.在跳高和标枪项目中,甲、乙的得分基本相同 C.甲的各项得分比乙更均衡 D.甲的总分高于乙的总分 ‎5.已知函数若则实数a的取值范围是 ‎ ‎ ‎ ‎ ‎6.任何一个复数(其中a,b∈R,i为虚数单位)都可以表示成(其中r≥0的形式,通常称之为复数z的三角形式.法国数学家棣莫弗发现:,我们称这个结论为棣莫弗定理.由棣莫弗定理可知,“n为偶数”是“复数为纯虚数的是 A充分不必要条件B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎7.已知点A,B,C均在半径为的圆上则的最大值为 ‎ C.4 D.‎ ‎8.在三棱锥P-ABC中若该三棱锥的体积为,则其外接球表面积的最小值为 A.5π B.C.D.‎ 二、多项选择题:本题共4小题,每小题5分,共20分在每小题给出的四个选项中,有多项符合题目要求全部选对的得5分,部分选对的得3分,有选错的得0分.‎ ‎9.已知在某市的一次学情检测中,学生的数学成绩X服从正态分布N(100,100),其中90分为及格线,120分为优秀线下列说法正确的是 附:随机变量ξ服从正态分布则 A.该市学生数学成绩的期望为100‎ B.该市学生数学成绩的标准差为100‎ C.该市学生数学成绩及格率超过0.8‎ D.该市学生数学成绩不及格的人数和优秀的人数大致相等 ‎10.已知圆锥的顶点为P,母线长为2,底面半径为,A,B为底面圆周上两个动点,则下列说法正确的是 A.圆锥的高为1‎ B.三角形PAB为等腰三角形 C.三角形PAB面积的最大值为 D.直线PA与圆锥底面所成角的大小为 ‎11.已知实数满足,则下列关系式中可能成立的是 Ax>y>zB.x>z>yC.z>x>yD.z>y>x ‎12.已知函数恒成立,且区间上单调,则下列说法正确的是 A.存在φ,使得是偶函数 ‎ C.ω是奇数 D.ω的最大值为3‎ 三、填空题:本题共4小题,每小题5分,共20分.‎ ‎13.5G指的是第五代移动通信技术,比第四代移动通信技术的数据传输速率快数百倍,某公司在研发‎5G项目时遇到一项技术难题,由甲、乙两个部门分别独立攻关,已知甲部门攻克该技术难题的概率为0.6,乙部门攻克该技术难题的概率为0.5.则该公司攻克这项技术难题的概率为 ‎14.能够说明“若,则a

查看更多