河南省郑州市示范性高中2021届高三数学(文)上学期阶段性考试(三)(Word版附答案)
www.ks5u.com
2020~2021年度河南省高三阶段性考试(三)
数学(文科)
考生注意:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分。考试时间120分钟。
2.请将各题答案填写在答题卡上。
3.本试卷主要考试内容:集合与常用逻辑用语,函数与导数,三角函数,解三角形。
第I卷
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合A={x|x<1},B={x|x2+x-6<0},则A∩B中整数元素的个数为
A.1 B.2 C.3 D.4
2.若α是第三象限角,则点(tan(3π-α),cos(π+α))在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在△ABC中,A=,AB=4,BC=,B
b3”是“a>b”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
5.函数f(x)=x2sinx-xcosx在[-π,π]上的图象大致为
6.设集合A={y|y=x2-4x+a},B={y|y=-sin2x+2sinx},若A∪B=A,则a的取值范围是
A.(-∞,5] B.[1,+∞) C.(-∞,1] D.[5,+∞)
7.某艺术展览馆在开馆时间段(9:00-16:00)的参观人数(单位:千)随时间t(单位:时)的变化近似满足函数关系f(t)=Asin(t-)+5(A>0,9≤t≤16),且下午两点整参观人数为7千,则开馆中参观人数的最大值为
A.7千 B.8千 C.9千 D.1万
8.若tan2x-tan(x+)=5,则tanx=
A. B. C. D.
9.已知函数f(x)=x4+x+1-a。设命题p:a∈(0,+∞),f(x)在R上至少有两个零点,关于命题p有以下四个判断:
①p为真命题; ②p为a∈(0,+∞),f(x)在R上至多有一个零点;
③p为假命题; ④p为a∈(0,+∞),f(x)在R上至多有两个零点。
其中判断正确的序号是
A.①② B.②③ C.③④ D.①④
10.太阳是位于太阳系中心的恒星,其质量M大约是2×1030千克地球是太阳系八大行星之一,其质量m大约是6×1024千克下列各数中与最接近的是(参考数据:lg3≈0.4771,lg6≈0.7782)
A.10-5.519 B.10-5.521 C.10-5.523 D.10-5.525
11.已知函数f(x)=x3-(3a+)x2+6ax,若f(x)在(-1,+∞)上既有极大值,又有最小值,且最小值为3a-,则a的取值范围为
A.(-,) B.(-,-) C.(-,-] D.(-,)
12.已知函数f(x)=x2-2x,若u∈log827,b=log511,c=-log0.358,则
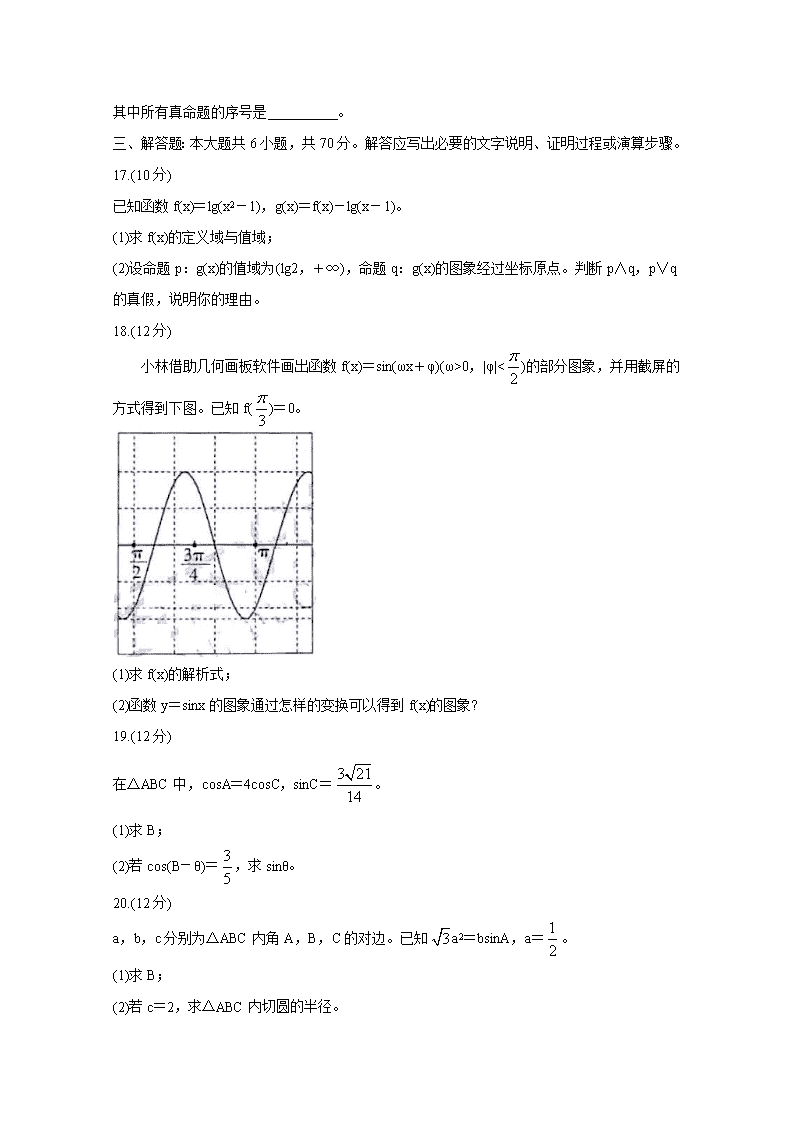
A.f(c)0,|φ|<)的部分图象,并用截屏的方式得到下图。已知f()=0。
(1)求f(x)的解析式;
(2)函数y=sinx的图象通过怎样的变换可以得到f(x)的图象?
19.(12分)
在△ABC中,cosA=4cosC,sinC=。
(1)求B;
(2)若cos(B-θ)=,求sinθ。
20.(12分)
a,b,c分别为△ABC内角A,B,C的对边。已知a2=bsinA,a=。
(1)求B;
(2)若c=2,求△ABC内切圆的半径。
21.(12分)
已知函数f(x)=(x2-3x+a)ex。
(1)若f(x)的极小值点小于2,求a的取值范围;
(2)设函数g(x)=af(x)(a≠0),讨论g(x)在(0,+∞)上的单调性。
22.(12分)
已知函数f(x)=。
(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)>0,求a的取值范围。