- 2021-06-16 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学选修2-1公开课课件3_1_2空间向量的数乘运算(2)
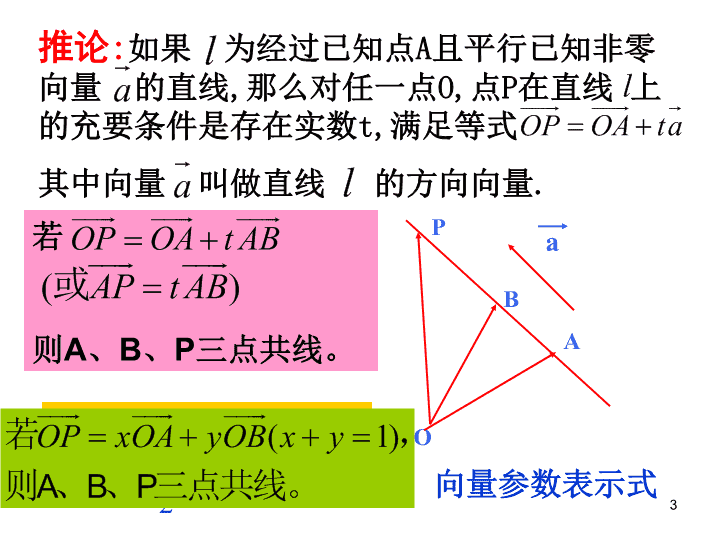
3.1.2 空间向量的 数乘运算(二) 2 一、共线向量 : 零向量与任意向量共线 . 1. 共线向量 : 如果表示空间向量的有向线段所在直线互相平行或重合 , 则这些向量叫做共线向量 ( 或平行向量 ), 记作 2. 共线向量定理 : 对空间任意两个向量 的充要条件是存在实数 使 3 O A B P a 若 P 为 A,B 中点 , 则 向量参数表示式 推论 : 如果 为经过已知点 A 且平行已知非零向量 的直线 , 那么对任一点 O, 点 P 在直线 上的充要条件是存在实数 t, 满足等式 其中向量 叫做直线 的方向向量 . 若 则 A 、 B 、 P 三点共线。 3—1—2 空间向量的基本定理 —— 共面向量定理 共面向量 : 平行于同一平面的向量 , 叫做共面向量 . O A 注意: 空间任意两个向量是共面的 ,但空间任意三个向量就不一定共面的了。 5 1 、如果向量 e 1 和 e 2 是一平面内的两个不平行的向量,那么,该平面内的任一向量 a 与 e 1 , e 2 有什么关系 ? 如果 e 1 和 e 2 是一平面内的两个不平行的向量,那么,该平面内的任一向量 a , 存在惟一的一对实数 a 1 , a 2 , 使 a = a 1 e 1 + a 2 e 2 2 、平面向量基本定理 复习: 6 ( 1 ) 必要性: 如果向量 c 与向量 a , b 共面, 则通过平移一定可以使他们位于同一平面内, 由平面向量基本定理可知, 一定存在唯一的实数对 x , y , 使 c = x a + y b 3 、共面向量定理: 如果两个向量 a , b 不共线 ,则向量 c 与向量 a , b 共面的充要条件是,存在 唯一 的一对实数 x , y ,使 c = x a + y b 证明: ( 2 ) 充分性: 如果 c 满足关系式 c = x a + y b , 则可选定一点 O ,作 OA = x a , OB = AC = y b ,于是 OC = OA + AC = x a + y b = c , 显然 OA , OB , OC ,都在平面 OAB 内 , 故 c , a , b 共面 B A C O c 7 共面向量定理的剖析 如果两个向量 a , b 不共线 , ★ 向量 c 与向量 a , b 共面 存在唯一的一对实数 x , y ,使 c = x a + y b ★ c = x a + y b 向量 c 与向量 a , b 共面 ( 性质 ) ( 判定 ) 8 9 思考 2 (课本 P88 思考) 即, P 、 A 、 B 、 C 四点共面。 10 得证 . 为什么 ? 11 例 1 、已知 A , B , C 三点不共线,对平面 ABC 外的任一点 O ,确定在下列条件下, M 是否与 A , B , C 三点共面: 12 例 2( 课本例 ) 如图,已知平行四边形 ABCD, 从平 面 AC 外一点 O 引向量 , , , , 求证: ⑴四点 E 、 F 、 G 、 H 共面; ⑵平面 EG// 平面 AC . 13 例 2 ( 课本例 ) 已知 ABCD ,从平面 AC 外一点 O 引向量 求证:①四点 E 、 F 、 G 、 H 共面; ② 平面 AC // 平面 EG. 证明: ∵ 四边形 ABCD 为 ① ∴ ( ﹡ ) ( ﹡ )代入 所以 E 、 F 、 G 、 H 共面。 14 例 2 已知 ABCD ,从平面 AC 外一点 O 引向量 求证:①四点 E 、 F 、 G 、 H 共面; ② 平面 AC // 平面 EG 。 证明: 由面面平行判定定理的推论得: ② 由①知 15 1. 对于空间任意一点 O ,下列命题正确的是: (A) 若 ,则 P 、 A 、 B 共线 (B) 若 ,则 P 是 AB 的中点 (C) 若 ,则 P 、 A 、 B 不共线 (D) 若 ,则 P 、 A 、 B 共线 2. 已知点 M 在平面 ABC 内,并且对空间任意一点 O , , 则 x 的值为 ( ) 16 1. 下列 说明正确的是: (A) 在平面内共线的向量在空间不一定共线 (B) 在空间共线的向量在平面内不一定共线 (C) 在平面内共线的向量在空间一定不共线 (D) 在空间共线的向量在平面内一定共线 2. 下列说法正确的是: (A) 平面内的任意两个向量都共线 (B) 空间的任意三个向量都不共面 (C) 空间的任意两个向量都共面 (D) 空间的任意三个向量都共面 17 例 3 : 已知斜三棱柱 ABC-A ’ B ’ C ’ ,设 AB = a , AC = b , AA ’ = c ,在面对角线 AC ’ 上和棱 BC 上分别取点 M 和 N ,使 AM = kAC ’ , BN = kBC ( 0≤k≤1 )。 求证: MN 与向量 a 和 c 共面 变式: 求证: MN∥ 平面 ABB ’ A ’ M N C B A ’ C ’ B ’ a c b A查看更多