2021届高考数学一轮复习第八章立体几何第5讲直线平面垂直的判定与性质课件

2021届高考数学一轮复习第八章立体几何第5讲直线平面垂直的判定与性质课件

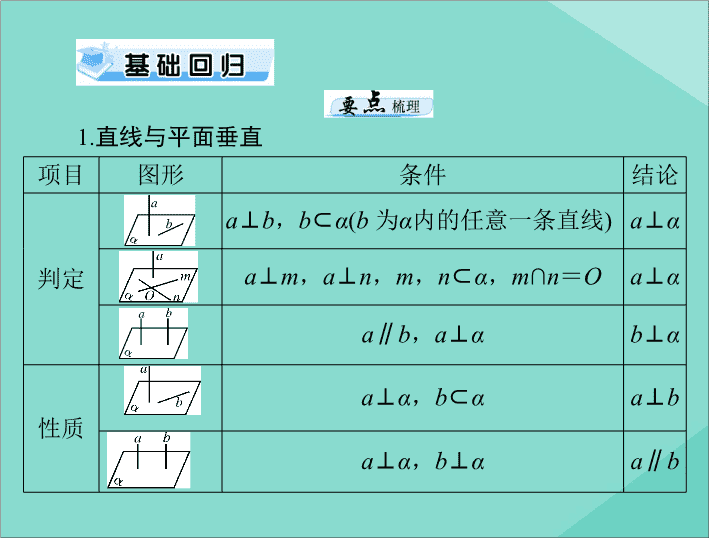
第 5 讲 直线、平面垂直的判定与性质 课标要求 考情风向标 1. 通过直观感知、操作确认，归纳出以 下判定定理： ◆ 一条直线与一个平面内的两条相交 直线垂直，则该直线与此平面垂直 . ◆ 一个平面过另一个平面的垂线，则 两个平面垂直 . 2. 通过直观感知、操作确认，归纳出以 下性质定理，并加以证明： ◆ 垂直于同一个平面的两条直线平行 . ◆ 两个平面垂直，则一个平面内垂直于 交线的直线与另一个平面垂直 . 3. 能运用已获得的结论证明一些空间位 置关系的简单命题 1. 垂直是立体几何的必考题目， 且几乎每年都有一个解答题出 现，所以它是高考的热点，是复 习的重点 . 纵观历年来的高考 题，立体几何中没有难度过大的 题，因此复习要抓好三基：基础 知识，基本方法， 基本能力 . 2. 要重视和研究数学思想、数学 方法 . 在本节中“化归”思想尤 为重要， 不论何种 “ 垂直 ” 都要 化归到 “ 线线垂直 ” ，观察与分 析几何体中线与线的关系是解 题的突破口 项目 图形 条件 结论 判定 a ⊥ b ， b ⊂ α ( b 为 α 内的任意一条直线 ) a ⊥ α a ⊥ m ， a ⊥ n ， m ， n ⊂ α ， m ∩ n ＝ O a ⊥ α a ∥ b ， a ⊥ α b ⊥ α 性质 a ⊥ α ， b ⊂ α a ⊥ b a ⊥ α ， b ⊥ α a ∥ b 1. 直线与平面垂直 定理 文字语言 图形语言 符号语言 判定 定理 如果一个平面经过另一 个平面的一条垂线，那么 这两个平面互相垂直 ⇒ α ⊥ β 性质 定理 如果两个平面垂直，那么 在一个平面内垂直于它 们交线的直线垂直于另 一个平面 2. 平面与平面垂直 ⇒ l ⊥ α 3. 直线与平面所成的角 (1) 如果直线与平面平行或者在平面内，那么直线与平面所 成的角等于 0°. (2) 如果直线和平面垂直，那么直线与平面所成的角等 于 90°. (3) 平面的斜线与它在平面上的射影所成的锐角叫做这条 斜线与平面所成的角，其范围是 (0° ， 90°). 斜线与平面所成的线 面角是这条斜线和平面内经过斜足的直线所成的一切角中最小 的角 . 4. 二面角 从一条直线出发的两个半平面组成的图象叫做二面角 . 从 二面角的棱上任意一点为端点，在两个面内 分别作垂直于棱的 两条射线，这两条射线所成的角叫做二面角的平面角 . 平面角是 直角的二面角叫做直二面角 . 1.(2019 年北京 ) 已知 l ， m 是平面 α 外的两条不同直线 . 给出 下列三个论断： ① l ⊥ m ； ② m ∥ α ； ③ l ⊥ α . 以其中的两个论断作为条件，余下的一个论断作为结论， 写出一个正确的命题： ____________________________. 解析： 将所给论断，分别作为条件、结论，得到如下三个 命题： (1) 如果 l ⊥ α ， m ∥ α ，那么 l ⊥ m . 正确； (2) 如果 l ⊥ α ， l ⊥ m ，那么 m ∥ α . 不正确，有可能 m 在平面 α 内； (3) 如果 l ⊥ m ， m ∥ α ，那么 l ⊥ α . 不正确，有可能 l 与 α 斜交， l ∥ α . 答案： 如果 l ⊥ α ， m ∥ α ，那么 l ⊥ m 2.(2017 年新课标 Ⅲ ) 在正方体 AB CD - A 1 B 1 C 1 D 1 中， E 为棱 ) C CD 的中点，则 ( A. A 1 E ⊥ DC 1 C. A 1 E ⊥ BC 1 B. A 1 E ⊥ BD D. A 1 E ⊥ AC ) 3. 在如图所示的四个正方体中，能得出 AB ⊥ CD 的是 ( A C B D A 4.(2019 年浙江模拟 ) 已知互相垂直的平面 α ， β 交于直线 l . ) C 解析： ∵ α ∩ β ＝ l ， ∴ l ⊂ β ， ∵ n ⊥ β ， ∴ n ⊥ l . 故选 C. 若直线 m ， n 满足 m ∥ α ， n ⊥ β ，则 ( A. m ∥ l B. m ∥ n C. n ⊥ l D. m ⊥ n 考点 1 直线与平面垂直的判定与性质 例 1 ： (1) 如图 8-5-1 ， PA ⊥⊙ O 所在平面， AB 是 ⊙ O 的直 径， C 是 ⊙ O 上一点， AE ⊥ PC ， AF ⊥ PB . 给出下列结论： ① AE ⊥ BC ； ② EF ⊥ PB ； ③ AF ⊥ BC ； ④ AE ⊥ 平面 PBC . 其中真命题 的序号是 __________. 图 8-5-1 解析： ① AE ⊂ 平面 PAC ， BC ⊥ AC ， BC ⊥ PA ⇒ AE ⊥ BC ，故 ① 正确； ② AE ⊥ PC ， AE ⊥ BC ， PB ⊂ 平面 PBC ⇒ AE ⊥ PB ， AF ⊥ PB ， EF ⊂ 平面 AEF ⇒ EF ⊥ PB ，故 ② 正确； ③ 若 AF ⊥ BC ⇒ AF ⊥ 平面 PBC ，则 AF ∥ AE ，与已知矛盾，故 ③ 错误；由 ① 可 知 ④ 正确 . 答案： ①②④ (2)( 多选 ) 如图 8-5-2 ，在四棱锥 P - ABCD 中，底面 ABCD 为 菱形， ∠ DAB ＝ 60° ，侧面 PAD 为正三角形，且平面 PAD ⊥ 平 面 ABCD ，则下列说法正确的是 ( ) 图 8-5-2 A. 在棱 AD 上存在点 M ，使 AD ⊥ 平面 PMB B. 异面直线 AD 与 PB 所成的角为 90° C. 二面角 P - BC - A 的大小为 45° D. BD ⊥ 平面 PAC 解析： 对于 A 项，如图 D83 ，取 AD 的中点 M ，连接 PM ， BM .∵ 侧面 PAD 为正三角形， 图 D83 ∴ PM ⊥ AD . 又底面 ABCD 是 ∠ DAB ＝ 60° 的菱形， ∴△ ABD 是等边三角形 . ∴ AD ⊥ BM .∴ AD ⊥ 平面 PBM . 故 A 项正确； 对于 B 项， ∵ AD ⊥ 平面 PBM ， ∴ AD ⊥ PB . 即异面直线 AD 与 PB 所成的角为 90°. 故 B 项正确； 对于 C 项，由 A 项知， AD ⊥ 平面 PBM ， ∴ BC ⊥ 平面 PBM . 则 ∠ PBM 是二面角 P - BC - A 的平面角 . ∴ 二面角 P - BC - A 的大小为 45° ，故 C 项正确 . 答案： ABC (3)(2019 年新课标 Ⅱ ) 如图 8-5-3 ，长方体 ABCD - A 1 B 1 C 1 D 1 的底面 ABCD 是正方形，点 E 在棱 AA 1 上， BE ⊥ EC 1 . ① 证明： BE ⊥ 平面 EB 1 C 1 ； ② 若 AE ＝ A 1 E ， AB ＝ 3 ，求四棱锥 E - BB 1 C 1 C 的体积 . 图 8-5-3 ① 证明： 由已知得 B 1 C 1 ⊥ 平面 ABB 1 A 1 ， BE ⊂ 平面 ABB 1 A 1 ， 故 B 1 C 1 ⊥ BE . 又 BE ⊥ EC 1 ， ∴ BE ⊥ 平面 EB 1 C 1 . ② 解： 由 ① 知 ∠ B EB 1 ＝ 90°. 由题设知 Rt△ ABE ≌ Rt A 1 B 1 E ， ∴∠ AEB ＝ ∠ A 1 EB 1 ＝ 45° ， 故 AE ＝ AB ＝ 3 ， AA 1 ＝ 2 AE ＝ 6. 作 EF ⊥ BB 1 ，垂足为 F ，则 EF ⊥ 平面 BB 1 C 1 C ，且 EF ＝ AB ＝ 3( 如图 D84). 图 D84 【 规律方法 】 直线与直线垂直 ⇒ 直线与平面垂直 ⇒ 平面与 平面垂直 ⇒ 直线与平面垂直 ⇒ 直线 与直线垂直，通过直线与平 面位置关系的不断转化来处理有关垂直的问题 . 出现中点时，平 行要联想到三角形中位线，垂直要联想到三角形的高；出现圆 周上的点时，联想到直径所对的圆周角为直角 . 考点 2 平面与平面垂直的判定与性质 例 2 ： (1) (2018 年新课标 Ⅰ ) 如图 8-5-4 ，在平行四边形 ABCM 中， AB ＝ AC ＝ 3 ， ∠ ACM ＝ 90° ，以 AC 为折痕将 △ ACM 折起， 使点 M 到达点 D 的位置，且 AB ⊥ DA . ① 证明：平面 ACD ⊥ 平面 ABC ； ② Q 为线段 AD 上一点， P 为线段 BC 上一点，且 BP ＝ DQ 图 8-5-4 ① 证明： 由已知可得， ∠ BAC ＝ 90° ， BA ⊥ AC . 又 BA ⊥ AD ， AC ∩ AD ＝ A ， ∴ AB ⊥ 平面 ACD . 又 AB ⊂ 平面 ABC ， ∴ 平面 ACD ⊥ 平面 ABC . 图 D85 (2)(2017 年新课标 Ⅰ ) 如图 8-5-5 ，在四棱锥 P - ABCD 中， AB ∥ CD ，且 ∠ BAP ＝ ∠ CDP ＝ 90°. ① 证明：平面 PAB ⊥ 平面 PAD ； 图 8-5-5 ① 证明： 由已知 ∠ BAP ＝ ∠ CDP ＝ 90° ，得 AB ⊥ AP ， CD ⊥ PD . 由于 AB ∥ CD ，故 AB ⊥ PD . 又 AP ∩ PD ＝ P ， ∴ AB ⊥ 平面 PAD . 又 AB ⊂ 平面 PAB ， ∴ 平面 PAB ⊥ 平面 PAD . 图 D86 【 规律方法 】 垂直、平行关系证明中应用转化与化归思想 的常见类型 . ① 证明线面、面面平行，需转化为证明线线平行 . ② 证明线面垂直，需转化为证明线线垂直 . ③ 证明线线垂直，需转化为证明线面垂直 . ④ 证明面面垂直，需转化为证明线面垂直，进而转化为证 明线线垂直 . 考点 3 线面所成的角 例 3 ： (20 18 年新课标 Ⅰ ) 在长方体 ABCD - A 1 B 1 C 1 D 1 中， AB ＝ BC ＝ 2 ， AC 1 与平面 BB 1 C 1 C 所成的角为 30° ，则该长方体的 体积为 ( ) 解析： 如图 8-5-6 ， ∠ AC 1 B 为 AC 1 与平面 BB 1 C 1 C 所成的角 为 30° ， 图 8-5-6 答案： C 【 规律方法 】 求线面角，关键作出射影，即面的垂线，可 利用面面垂直的性质定理得到线面垂直，即面的垂线： AB ⊥ 平 面 BB 1 C 1 C ，从而直线 AC 1 与平面 BB 1 C 1 C 所成角即为 ∠ AC 1 B . 【 跟踪训练 】 1.(2019 年天津 ) 如图 8-5 -7 ，在四棱锥 P - ABCD 中，底面 ABCD 为平行四边形， △ PCD 为等边三角形，平面 PAC ⊥ 平面 PCD ， PA ⊥ CD ， CD ＝ 2 ， AD ＝ 3. 图 8-5-7 (1) 设 G ， H 分别为 PB ， AC 的中点，求证： GH ∥ 平面 PAD ； (2) 求证： PA ⊥ 平面 PCD ； (3) 求直线 AD 与平面 PAC 所成角的正弦值 . (1) 证明： 如图 D87 ，连接 BD ，易知 AC ∩ BD ＝ H ， BH ＝ DH . 又由 BG ＝ PG ，故 GH ∥ PD . 又 ∵ GH ⊄ 平面 PAD ， PD ⊂ 平面 PAD ， ∴ GH ∥ 平面 PAD . 图 D87 (2) 证明： 取棱 PC 的中点 N ，连接 DN . 依题意，得 DN ⊥ PC ， 又 ∵ 平面 PAC ⊥ 平面 PCD ，平面 PAC ∩ 平面 PCD ＝ PC ， ∴ DN ⊥ 平面 PAC ，又 PA ⊂ PAC ，故 DN ⊥ PA . 又 PA ⊥ CD ， CD ∩ DN ＝ D ， ∴ PA ⊥ 平面 PCD . (3) 解： 连接 AN ，由 (2) 中 DN ⊥ 平面 PAC ， 知 ∠ DAN 为直线 AD 与平面 PAC 所成的角， ∵△ PCD 为等边三角形， CD ＝ 2 ，且 N 为 PC 的中点， 难点突破 ⊙ 面面所成的角 例题： (2018 年浙江 ) 已知四棱锥 S - ABCD 的底面是正方形 ， 侧棱长 均相等， E 是线段 AB 上的点 ( 不含端点 ) ，设 SE 与 BC 所成的角为 θ 1 ， SE 与平面 ABCD 所成的角为 θ 2 ，二面角 S - AB - C ) 的平面角为 θ 3 ，则 ( A. θ 1 ≤ θ 2 ≤ θ 3 C. θ 1 ≤ θ 3 ≤ θ 2 B. θ 3 ≤ θ 2 ≤ θ 1 D. θ 2 ≤ θ 3 ≤ θ 1 解析： 设 O 为正方形 ABCD 的中心， M 为 AB 中点，过 E 作 BC 的平行线 EF ，交 CD 于 F ，过 O 作 ON ⊥ EF 于 N ，连接 SO ， SN ， OM ，则 SO ⊥ 底面 ABCD ， OM ⊥ AB ， 因此 ∠ SEN ＝ θ 1 ， ∠ SEO ＝ θ 2 ， ∠ SMO ＝ θ 3 ， ∵ SN ≥ SO ， EO ≥ OM ， ∴ tan θ 1 ≥tan θ 3 ≥tan θ 2 ，即 θ 1 ≥ θ 3 ≥ θ 2 . 故选 D. 答案： D 【 跟踪训练 】 2.(2019 年浙江 ) 设三棱锥 V - ABC 的底面是正三角形，侧棱 长均相等， P 是棱 VA 上的点 ( 不含端点 ) ，记直线 PB 与直线 AC 所成角为 α ，直线 PB 与平面 ABC 所成角为 β ，二面角 P - AC - B ) 的平面角为 γ ，则 ( A. β < γ ， α < γ C. β < α ， γ < α B. β < α ， β < γ D. α < β ， γ < β 图 D88 方法二，由最小角定理 β < α ，记 V - AB - C 的平面角为 γ ′( 显 然 γ ′ ＝ γ ) 由最大角定理 β < γ ′ ＝ γ ，故选 B. 答案： B 1. 证明线面垂直的方法 . (1) 用线面垂直的定义：若一直线垂直于平面内任一直线， 这条直线垂直于该平面； (2) 用线面垂直的判定定理：若一直线垂直于平面内两条相 交直线，这条直线垂直于该平面； (3) 用线面垂直的性质定理：若两平行直线之一垂直于平 面，则另一条直线也垂直于该平面； (4) 用面面垂直的性质定理：若两个平面垂直，在一个平面 内垂直于交线的直线必垂直于另一个平面； (5) 如果一条直线垂直于两个平行平面中的一个，那么也垂 直于另一个平面； (6) 如果两个相交平面都和第三个平面垂直，那么相交平面 的交线也垂直于第三个平面 . 2. 判定面面垂直的方法 . (1) 定义法 . 首先找二面角 的平面角，然后证明其为直角； (2) 利用面面垂直的判定定理：一个平面经过另一个平面 的 一条垂线 . 3. 垂直于同一个平面的两条直线平行，是判定两条直线平 行的又一重要方法，是实现空间中平行关系和垂直关系在一定 条件下相互转化的一种手段 . 4. 几个常用的结论 . (1) 过空间任一点有且只有一条直线与已知平面垂直； (2) 过空间任一点有且只有一个平面与已知直线垂直； (3) 垂直于同一直线的两个平面互相平行 . 5. 空间中直线与直线垂直、直线与平面垂直、平面与平面 垂直三者之间可以相互转化，每一种垂直的判定都是从某种垂 直开始转向另一种垂直最终达到目的，其转化关系为： 在证明两平面垂直时一般先从现有的直线中寻找平面的垂 线，若这样的直线图中不存在，则可通过作辅助线来解决 .