2021高考数学大一轮复习单元质检十二概率B理新人教A版
单元质检十二 概率(B)
(时间:45分钟 满分:100分)
单元质检卷第24页
一、选择题(本大题共6小题,每小题7分,共42分)
1.若随机变量X~B(100,p),X的均值E(X)=24,则p的值是( )
A.25 B.35
C.625 D.1925
答案:C
解析:∵X~B(100,p),
∴E(X)=100p.
又E(X)=24,
∴24=100p,
即p=24100=625.
2.两名教师对一篇初评为“优秀”的作文复评,若批改成绩都是两位正整数,且十位数字都是5,则两名教师批改成绩之差的绝对值不超过2的概率为( )
A.0.44 B.0.56 C.0.41 D.0.39
答案:A
解析:用(x,y)表示两名教师的批改成绩,则(x,y)的所有可能情况为10×10=100(种).
当x=50时,y可取50,51,52,共3种可能;
当x=51时,y可取50,51,52,53,共4种可能;
当x=52,53,54,55,56,57时,y的取法均有5种,共30种可能;
当x=58时,y可取56,57,58,59,共4种可能;
当x=59时,y可取57,58,59,共3种可能.
综上可得,两名教师批改成绩之差的绝对值不超过2的情况有44种.
8
由古典概型概率公式可得,所求概率P=44100=0.44.
3.甲、乙两人独立地对同一目标各射击一次,命中率分别为0.6和0.7,在目标被击中的情况下,甲、乙同时击中目标的概率为( )
A.2144 B.1522
C.2150 D.925
答案:A
解析:(方法一)设“目标被击中”为事件B,“甲、乙同时击中目标”为事件A,
则P(A)=0.6×0.7=0.42,P(B)=0.6×0.7+0.4×0.7+0.6×0.3=0.88,
得P(A|B)=P(AB)P(B)=P(A)P(B)=0.420.88=2144.
(方法二)记“甲击中目标”为事件A,“乙击中目标”为事件B,“目标被击中”为事件C,
则P(C)=1-P(A)P(B)=1-(1-0.6)×(1-0.7)=0.88.
故在目标被击中的情况下,甲、乙同时击中目标的概率为0.6×0.70.88=2144.故选A.
4.七巧板是我国古代劳动人民的发明之一,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.一个用七巧板拼成的正方形如图所示,若在此正方形中任取一点,则此点取自阴影部分的概率是( )
A.14 B.18
C.38 D.316
答案:B
解析:不妨设小正方形的边长为1,则最小的两个等腰直角三角形的边长为1,1,2,左上角的等腰直角三角形的边长为2,2,2,两个最大的等腰直角三角形的边长为2,2,22,即大正方形的边长为22,所以所求概率
8
P=1-12×2+1+1+2×28=18.
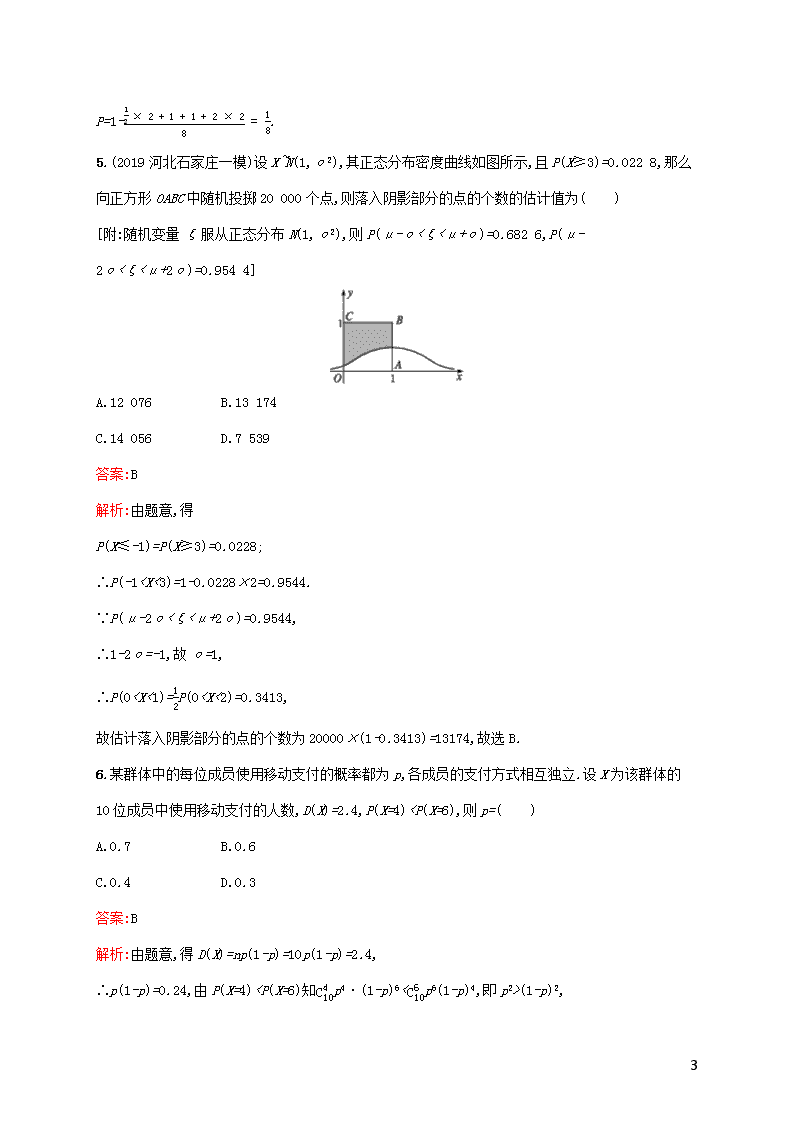
5.(2019河北石家庄一模)设X~N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)=0.022 8,那么向正方形OABC中随机投掷20 000个点,则落入阴影部分的点的个数的估计值为( )
[附:随机变量ξ服从正态分布N(1,σ2),则P(μ-σ<ξ<μ+σ)=0.682 6,P(μ-2σ<ξ<μ+2σ)=0.954 4]
A.12 076 B.13 174
C.14 056 D.7 539
答案:B
解析:由题意,得
P(X≤-1)=P(X≥3)=0.0228;
∴P(-1
(1-p)2,
8
∴p>0.5,
∴p=0.6(其中p=0.4舍去).
二、填空题(本大题共2小题,每小题7分,共14分)
7.(2019辽宁庄河高级中学一模)若10件产品包含2件次品,今在其中任取两件,则在已知两件中有一件不是次品的条件下,另一件是次品的概率为 .
答案:411
解析:设事件A={两件中有一件不是次品},事件B={两件中恰有一件是次品},则P(B|A)=P(AB)P(A)=P(B)P(A)=C21C81C102C82+C21C81C102=411.
8.甲、乙等5名志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.设随机变量X为这5名志愿者中参加A岗位服务的人数,则X的均值为 .
答案:54
解析:根据题意,5名志愿者被随机分配到A,B,C,D四个不同岗位,每个岗位至少一人,共有C52A44=240(种),而X=1,2,
则P(X=1)=C51C42A33240=180240=34,
P(X=2)=C52A33240=60240=14,
故E(X)=1×34+2×14=54.
三、解答题(本大题共3小题,共44分)
9.(14分)根据国家《环境空气质量》规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别
PM2.5/(微克/立方米)
频数/天
频率
第一组
[0,15)
4
0.1
8
第二组
[15,30)
12
0.3
第三组
[30,45)
8
0.2
第四组
[45,60)
8
0.2
第五组
[60,75)
4
0.1
第六组
[75,90]
4
0.1
(1)写出该样本的众数和中位数(不必写出计算过程);
(2)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(3)将频率视为概率,监测去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为ξ,求ξ的分布列及均值E(ξ)和方差D(ξ).
解:(1)众数为22.5微克/立方米,中位数为37.5微克/立方米.
(2)去年该居民区PM2.5的年平均浓度为7.5×0.1+22.5×0.3+37.5×0.2+52.5×0.2+67.5×0.1+82.5×0.1=40.5(微克/立方米).
∵40.5>35,
∴去年该居民区PM2.5的年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.
(3)记事件A表示“一天PM2.5的24小时平均浓度符合环境空气质量标准”,则P(A)=910.
随机变量ξ的可能取值为0,1,2,且ξ~B2,910.
∴P(ξ=k)=C2k910k1-9102-k(k=0,1,2),即
ξ
0
1
2
P
1100
18100
81100
∴E(ξ)=0×1100+1×18100+2×81100=1.8,
或E(ξ)=np=2×910=1.8,
D(ξ)=np(1-p)=2×910×110=0.18.
8
10.(15分)为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘制成折线图如下:
女生统计图
男生统计图
(1)已知该校有400名学生,试估计全校学生中,每天学习不足4小时的人数;
(2)若从学习时间不少于4小时的学生中选取4人,设选取的男生人数为X,求随机变量X的分布列及均值E(X);
(3)试比较男生学习时间的方差s12与女生学习时间的方差s22的大小.(只需写出结论)
解:(1)由折线图可得共抽取了20人,其中男生中学习时间不足4小时的有8人,女生中学习时间不足4小时的有4人.
故可估计全校学生中每天学习时间不足4小时的人数为400×1220=240.
(2)学习时间不少于4小时的学生共8人,其中男生人数为4,
故X的所有可能取值为0,1,2,3,4.
由题意可得
P(X=0)=C44C84=170,
P(X=1)=C41C43C84=1670=835,
P(X=2)=C42C42C84=3670=1835,
8
P(X=3)=C43C41C84=1670=835,
P(X=4)=C44C84=170.
所以随机变量X的分布列为
X
0
1
2
3
4
P
170
835
1835
835
170
∴均值E(X)=0×170+1×835+2×1835+3×835+4×170=2.
(3)由折线图可得s12>s22.
11.(15分)(2019全国Ⅰ,理21)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
①证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
②求p4,并根据p4的值解释这种试验方案的合理性.
解:(1)X的所有可能取值为-1,0,1.
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β).
8
所以X的分布列为
X
-1
0
1
P
(1-α)β
αβ+(1-α)(1-β)
α(1-β)
(2)①证明:由(1)得a=0.4,b=0.5,c=0.1.
因此pi=0.4pi-1+0.5pi+0.1pi+1,
故0.1(pi+1-pi)=0.4(pi-pi-1),
即pi+1-pi=4(pi-pi-1).
又因为p1-p0=p1≠0,
所以{pi+1-pi}(i=0,1,2,…,7)为公比为4,首项为p1的等比数列.
②由①可得p8=p8-p7+p7-p6+…+p1-p0+p0
=(p8-p7)+(p7-p6)+…+(p1-p0)
=48-13p1.
由于p8=1,故p1=348-1,
所以p4=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)=44-13p1=1257.
p4表示最终认为甲药更有效的概率.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为p4=1257≈0.0039,此时得出错误结论的概率非常小,说明这种试验方案合理.
8