2018届二轮复习导数及其应用课件理(全国通用)
第
3
讲 导数及其应用
-
2
-
热点考题诠释
高考方向解读
1
.
(2017
浙江
,7)
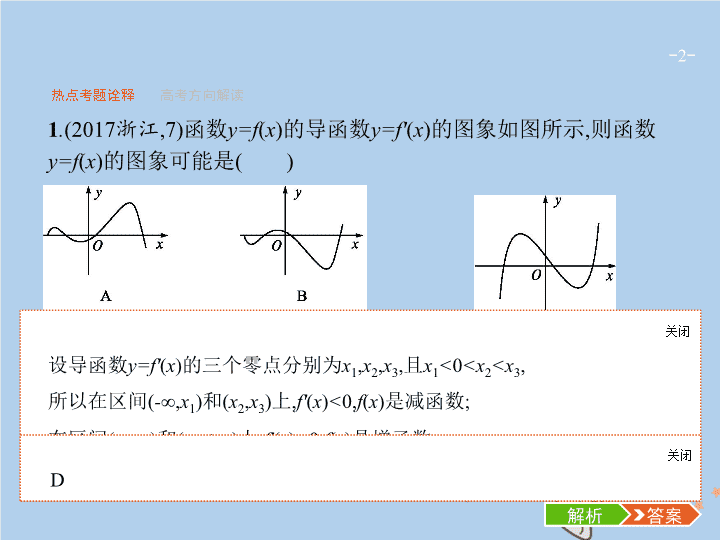
函数
y=f
(
x
)
的导函数
y=f'
(
x
)
的图象如图所示
,
则函数
y=f
(
x
)
的图象可能是
(
)
答案
解析
解析
关闭
设导函数
y=f'
(
x
)
的三个零点分别为
x
1
,
x
2
,
x
3
,
且
x
1
<
0
0,
f
(
x
)
是增函数
.
所以函数
y=f
(
x
)
的图象可能为
D
.
故选
D
.
答案
解析
关闭
D
-
3
-
热点考题诠释
高考方向解读
2
.
(2017
全国
2,
理
11)
若
x=-
2
是函数
f
(
x
)
=
(
x
2
+ax-
1)e
x-
1
的极值点
,
则
f
(
x
)
的极小值为
(
)
A
.-
1 B
.-
2e
-
3
C
.
5e
-
3
D
.
1
答案
解析
解析
关闭
答案
解析
关闭
-
4
-
热点考题诠释
高考方向解读
答案
解析
解析
关闭
答案
解析
关闭
-
5
-
热点考题诠释
高考方向解读
-
6
-
热点考题诠释
高考方向解读
-
7
-
热点考题诠释
高考方向解读
5
.
(2017
天津
,
理
20)
设
a
∈
Z
,
已知定义在
R
上的函数
f
(
x
)
=
2
x
4
+
3
x
3
-
3
x
2
-
6
x+a
在区间
(1,2)
内有一个零点
x
0
,
g
(
x
)
为
f
(
x
)
的导函数
.
(1)
求
g
(
x
)
的单调区间
;
(2)
设
m
∈
[1,
x
0
)
∪
(
x
0
,2],
函数
h
(
x
)
=g
(
x
)(
m-x
0
)
-f
(
m
),
求证
:
h
(
m
)
h
(
x
0
)
<
0;
(3)
求证
:
存在大于
0
的常数
A
,
使得对于任意的正整数
p
,
q
,
且
-
8
-
热点考题诠释
高考方向解读
-
9
-
热点考题诠释
高考方向解读
(2)
证明
由
h
(
x
)
=g
(
x
)(
m-x
0
)
-f
(
m
),
得
h
(
m
)
=g
(
m
)(
m-x
0
)
-f
(
m
),
h
(
x
0
)
=g
(
x
0
)(
m-x
0
)
-f
(
m
)
.
令函数
H
1
(
x
)
=g
(
x
)(
x-x
0
)
-f
(
x
),
则
H'
1
(
x
)
=g'
(
x
)(
x-x
0
)
.
由
(1)
知
,
当
x
∈
[1,2]
时
,
g'
(
x
)
>
0,
故当
x
∈
[1,
x
0
)
时
,
H'
1
(
x
)
<
0,
H
1
(
x
)
单调递减
;
当
x
∈
(
x
0
,2]
时
,
H'
1
(
x
)
>
0,
H
1
(
x
)
单调递增
.
因此
,
当
x
∈
[1,
x
0
)
∪
(
x
0
,2]
时
,
H
1
(
x
)
>H
1
(
x
0
)
=-f
(
x
0
)
=
0,
可得
H
1
(
m
)
>
0,
即
h
(
m
)
>
0
.
令函数
H
2
(
x
)
=g
(
x
0
)(
x-x
0
)
-f
(
x
),
则
H'
2
(
x
)
=g
(
x
0
)
-g
(
x
)
.
由
(1)
知
g
(
x
)
在
[1,2]
上单调递增
,
故当
x
∈
[1,
x
0
)
时
,
H'
2
(
x
)
>
0,
H
2
(
x
)
单调递增
;
当
x
∈
(
x
0
,2]
时
,
H'
2
(
x
)
<
0,
H
2
(
x
)
单调递减
.
因此
,
当
x
∈
[1,
x
0
)
∪
(
x
0
,2]
时
,
H
2
(
x
)
0,
且
m+
2
<
0,
所以
-
3
0,
令
f'
(
x
)
=
0,
则
x=
2,
∴
当
0
2
时
,
f'
(
x
)
>
0,
f
(
x
)
单调递增
.
∴
函数
f
(
x
)
的单调递减区间为
(0,2),
单调递增区间为
(2,
+∞
)
.
-
19
-
命题热点一
命题热点二
命题热点三
(2)
由
(1)
知
,
k
≤
0
时
,
函数
f
(
x
)
在区间
(0,2)
内单调递减
,
故函数
f
(
x
)
在区间
(0,2)
内不存在极值点
;
当
k>
0
时
,
设函数
g
(
x
)
=
e
x
-kx
,
x
∈
(0,
+∞
)
.
∵
g'
(
x
)
=
e
x
-k=
e
x
-
e
ln
k
,
当
0
0,
y=g
(
x
)
单调递增
,
故函数
f
(
x
)
在区间
(0,2)
内不存在两个极值点
;
当
k>
1
时
,
得
x
∈
(0,ln
k
)
时
,
g'
(
x
)
<
0,
函数
y=g
(
x
)
单调递减
,
x
∈
(ln
k
,
+∞
)
时
,
g'
(
x
)
>
0,
函数
y=g
(
x
)
单调递增
,
∴
函数
y=g
(
x
)
的最小值为
g
(ln
k
)
=k
(1
-
ln
k
),
函数
f
(
x
)
在区间
(0,2)
内存在两个极值点
,
-
20
-
命题热点一
命题热点二
命题热点三
-
21
-
命题热点一
命题热点二
命题热点三
-
22
-
命题热点一
命题热点二
命题热点三
-
23
-
命题热点一
命题热点二
命题热点三
-
24
-
命题热点一
命题热点二
命题热点三
规律方法
1
.
利用函数的导数研究函数的单调性的一般步骤
:
(1)
确定函数的定义域
.
(2)
求导数
f'
(
x
)
.
(3)
①
若求单调区间
(
或证明单调性
),
只需在函数
y=f
(
x
)
的定义域内解
(
或证明
)
不等式
f'
(
x
)
>
0
或
f'
(
x
)
<
0;
②
若已知
y=f
(
x
)
的单调性
,
则转化为不等式
f'
(
x
)
≥
0
或
f'
(
x
)
≤
0
在单调区间上恒成立问题求解
.
2
.
对于函数
y=f
(
x
),
若在点
x=a
处有
f'
(
a
)
=
0,
且在点
x=a
附近的左侧
f'
(
x
)
<
0,
右侧
f'
(
x
)
>
0,
则当
x=a
时
f
(
x
)
有极小值
f
(
a
);
若在点
x=b
处有
f'
(
b
)
=
0,
且在点
x=b
附近的左侧
f'
(
x
)
>
0,
右侧
f'
(
x
)
<
0,
则当
x=b
时
f
(
x
)
有极大值
f
(
b
)
.
-
25
-
命题热点一
命题热点二
命题热点三
3
.
求函数
y=f
(
x
)
在
[
a
,
b
]
上的最大值与最小值的步骤
:
(1)
求函数
y=f
(
x
)
在区间
(
a
,
b
)
内的极值
;
(2)
将函数
y=f
(
x
)
的各极值与端点处的函数值
f
(
a
),
f
(
b
)
比较
,
其中最大的一个是最大值
,
最小的一个是最小值
.
-
26
-
命题热点一
命题热点二
命题热点三
迁移训练
3
已知函数
f
(
x
)
的导数为
f'
(
x
),
f
(
x
)
不是常数函数
,
且
(
x+
1)
f
(
x
)
+xf'
(
x
)
≥
0
对
x
∈
[0,
+∞
)
恒成立
,
则下列不等式一定成立的是
(
)
A.
f
(1)
<
2e
f
(2) B.e
f
(1)
0)
-
38
-
命题热点一
命题热点二
命题热点三
3
.
利用导数证明不等式
,
主要是构造函数
.
通过导数判断函数的单调性
,
由函数的单调性证明不等式成立
,
或通过求函数的最值
,
当该函数的最大值或最小值可使不等式成立时
,
则不等式恒成立
,
从而可将不等式的证明转化到求函数的最值上来
.
不等式的恒成立问题和有解问题、无解问题的解题方法是依据不等式的特点
,
进行等价变形
.
构造函数
,
借助图象观察或参变分离
,
转化为求函数的最值问题
.
-
39
-
命题热点一
命题热点二
命题热点三
迁移训练
5
已知函数
f
(
x
)
=
(
t+
1)ln
x+tx
2
+
3
t
,
t
∈
R
.
(1)
若
t=
0,
求证
:
当
x
≥
0
时
,
f
(
x+
1)
≥
x- x
2
;
(2)
若
f
(
x
)
≥
4
x
对任意
x
∈
[1,
+∞
)
恒成立
,
求
t
的取值范围
.
-
40
-
命题热点一
命题热点二
命题热点三
-
41
-
答题规范提分
解答题解题过程要求
“
解答应写出文字说明、证明过程或演算步骤
”
,
因此
,
在解答题答题过程中应该有规范的书写步骤
,
分步得分
.
-
42
-
-
43
-
-
44
-
1
2
3
4
5
1
.
已知
a
∈
R
,
设函数
f
(
x
)
=ax-
ln
x
的图象在点
(1,
f
(1))
处的切线为
l
,
则
l
在
y
轴上的截距为
.
答案
解析
解析
关闭
答案
解析
关闭
-
45
-
1
2
3
4
5
2
.
若函数
e
x
f
(
x
)(e
=
2
.
718 28
…
是自然对数的底数
)
在
f
(
x
)
的定义域上单调递增
,
则称函数
f
(
x
)
具有
M
性质
.
下列函数中所有具有
M
性质的函数的序号为
.
①
f
(
x
)
=
2
-x
②
f
(
x
)
=
3
-x
③
f
(
x
)
=x
3
④
f
(
x
)
=x
2
+
2
答案
:
①④
-
46
-
1
2
3
4
5
∴
g
(
x
)
在
R
上单调递减
,
不具有
M
性质
;
对
③
,
设
g
(
x
)
=
e
x
·x
3
,
则
g'
(
x
)
=
e
x
·x
2
(
x+
3),
令
g'
(
x
)
=
0,
得
x
1
=-
3,
x
2
=
0,
∴
g
(
x
)
在
(
-∞
,
-
3)
上单调递减
,
在
(
-
3,
+∞
)
上单调递增
,
不具有
M
性质
;
对
④
,
设
g
(
x
)
=
e
x
(
x
2
+
2),
则
g'
(
x
)
=
e
x
(
x
2
+
2
x+
2),
∵
x
2
+
2
x+
2
=
(
x+
1)
2
+
1
>
0,
∴
g'
(
x
)
>
0,
∴
g
(
x
)
在
R
上单调递增
,
具有
M
性质
.
故填
①④
.
-
47
-
1
2
3
4
5
-
48
-
1
2
3
4
5
-
49
-
1
2
3
4
5
4
.
已知函数
f
(
x
)
=a
e
2
x
+
(
a-
2)e
x
-x.
(1)
讨论
f
(
x
)
的单调性
;
(2)
若
f
(
x
)
有两个零点
,
求
a
的取值范围
.
解
:
(1)
f
(
x
)
的定义域为
(
-∞
,
+∞
),
f'
(
x
)
=
2
a
e
2
x
+
(
a-
2)e
x
-
1
=
(
a
e
x
-
1)(2e
x
+
1)
.
(
ⅰ
)
若
a
≤
0,
则
f'
(
x
)
<
0,
所以
f
(
x
)
在
(
-∞
,
+∞
)
单调递减
.
(
ⅱ
)
若
a>
0,
则由
f'
(
x
)
=
0
得
x=-
ln
a.
当
x
∈
(
-∞
,
-
ln
a
)
时
,
f'
(
x
)
<
0;
当
x
∈
(
-
ln
a
,
+∞
)
时
,
f'
(
x
)
>
0,
所以
f
(
x
)
在
(
-∞
,
-
ln
a
)
单调递减
,
在
(
-
ln
a
,
+∞
)
单调递增
.
-
50
-
1
2
3
4
5
-
51
-
1
2
3
4
5
(1)
如果常数
k>
0,
求函数
f
(
x
)
在区间
(0,
k
]
上的最大值
;
(2)
对于
m>
0,
如果方程
2
mf
(
x
)
-x=
0
在
(0,
+∞
)
上有且只有一个解
,
求
m
的值
.
-
52
-
1
2
3
4
5