2019届二轮复习规范答题示例10　导数与不等式的恒成立问题课件（15张）（全国通用）

2019届二轮复习规范答题示例10　导数与不等式的恒成立问题课件（15张）（全国通用）

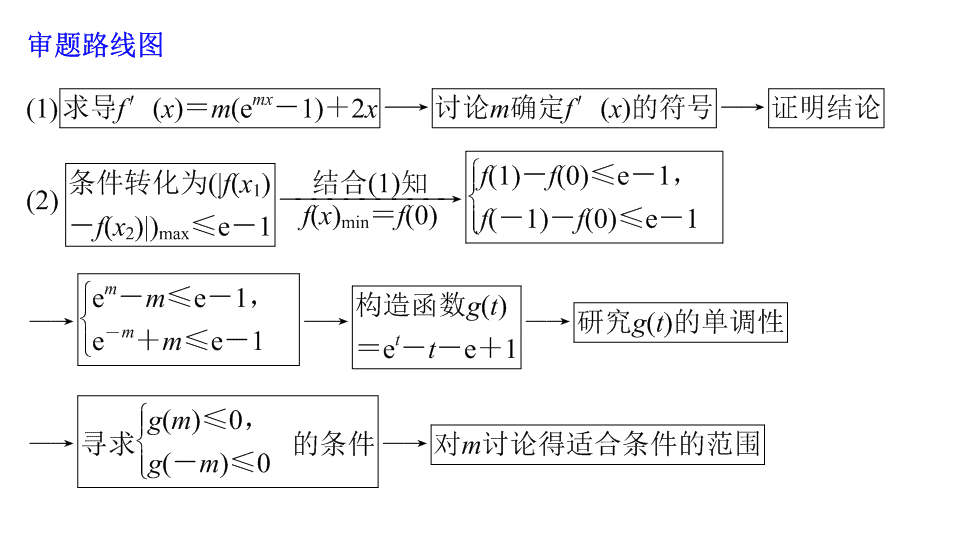
板块三　专题突破核心考点 导数与不等式的恒成立问题 规范答题示例 10 　 典例 10 　 (12 分 ) 设函数 f ( x ) ＝ e mx ＋ x 2 － mx . (1) 证明： f ( x ) 在 ( － ∞ ， 0) 上单调递减，在 (0 ，＋ ∞ ) 上单调递增； (2) 若对于任意 x 1 ， x 2 ∈ [ － 1,1] ，都有 | f ( x 1 ) － f ( x 2 )| ≤ e － 1 ，求 m 的取值范围 . 规 范 解 答 · 分 步 得 分 (1) 证明 　 f ′ ( x ) ＝ m (e mx － 1) ＋ 2 x . 1 分 若 m ≥ 0 ，则当 x ∈ ( － ∞ ， 0) 时， e mx － 1 ≤ 0 ， f ′ ( x )<0 ； 当 x ∈ (0 ，＋ ∞ ) 时， e mx － 1 ≥ 0 ， f ′ ( x )>0. 若 m <0 ，则当 x ∈ ( － ∞ ， 0) 时， e mx － 1>0 ， f ′ ( x )<0 ； 当 x ∈ (0 ，＋ ∞ ) 时， e mx － 1<0 ， f ′ ( x )>0 . 4 分 所以 f ( x ) 在 ( － ∞ ， 0) 上单调递减，在 (0 ，＋ ∞ ) 上单调 递增 . 6 分 (2) 解 　 由 (1) 知，对任意的 m ， f ( x ) 在 [ － 1,0] 上单调递减，在 [0,1] 上单调递增， 故 f ( x ) 在 x ＝ 0 处取得最小值 . 所以对于任意 x 1 ， x 2 ∈ [ － 1,1] ， | f ( x 1 ) － f ( x 2 )| ≤ e － 1 的充要条件是 设函数 g ( t ) ＝ e t － t － e ＋ 1 ，则 g ′ ( t ) ＝ e t － 1 . 9 分 当 t <0 时， g ′ ( t )<0 ；当 t >0 时， g ′ ( t )>0. 故 g ( t ) 在 ( － ∞ ， 0) 上单调递减，在 (0 ，＋ ∞ ) 上单调递增 . 又 g (1) ＝ 0 ， g ( － 1) ＝ e － 1 ＋ 2 － e<0 ，故当 t ∈ [ － 1,1] 时， g ( t ) ≤ 0 . 当 m ∈ [ － 1,1] 时， g ( m ) ≤ 0 ， g ( － m ) ≤ 0 ，即 ① 式成立 ； 10 分 当 m >1 时，由 g ( t ) 的单调性，得 g ( m )>0 ，即 e m － m >e － 1 ； 当 m < － 1 时， g ( － m )>0 ，即 e － m ＋ m >e － 1 . 11 分 综上， m 的取值范围是 [ － 1,1 ]. 12 分 构 建 答 题 模 板 第一步 求导数： 一般先确定函数的定义域，再求 f ′ ( x ). 第二步 定区间： 根据 f ′ ( x ) 的符号确定函数的单调性 . 第三步 寻条件： 一般将恒成立问题转化为函数的最值问题 . 第四步 写步骤： 通过函数单调性探求函数最值，对于最值可能在两点取到的恒成立问题，可转化为不等式组恒成立 . 第五步 再反思： 查看是否注意定义域、区间的写法、最值点的探求是否合理等 . 评分细则 　 (1) 求出导数给 1 分； (2) 讨论时漏掉 m ＝ 0 扣 1 分；两种情况只讨论正确一种给 2 分； (3) 确定 f ′ ( x ) 符号时只有结论无中间过程扣 1 分； (4) 写出 f ( x ) 在 x ＝ 0 处取得最小值给 1 分； (5) 无最后结论扣 1 分； (6) 其他方法构造函数同样给分 . 解答 跟踪演练 10 　 (2018· 全国 Ⅰ ) 已知函数 f ( x ) ＝ － x ＋ a ln x . (1) 讨论 f ( x ) 的单调性； 解　 f ( x ) 的定义域为 (0 ，＋ ∞ ) ， ① 若 a ≤ 2 ，则 f ′ ( x ) ≤ 0 ， 当且仅当 a ＝ 2 ， x ＝ 1 时， f ′ ( x ) ＝ 0 ，所以 f ( x ) 在 (0 ，＋ ∞ ) 上单调递减 . ② 若 a >2 ，令 f ′ ( x ) ＝ 0 ，得 证明 证明　 由 (1) 知， f ( x ) 存在两个极值点当且仅当 a >2. 由于 f ( x ) 的两个极值点 x 1 ， x 2 满足 x 2 － ax ＋ 1 ＝ 0 ， 所以 x 1 x 2 ＝ 1 ，不妨设 0< x 1 < x 2 ，则 x 2 >1. 由 (1) 知， g ( x ) 在 (0 ，＋ ∞ ) 上单调递减， 又 g (1) ＝ 0 ，从而当 x ∈ (1 ，＋ ∞ ) 时， g ( x )<0.