- 2021-06-16 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习对数的概念和运算性质课件(14张)(全国通用)
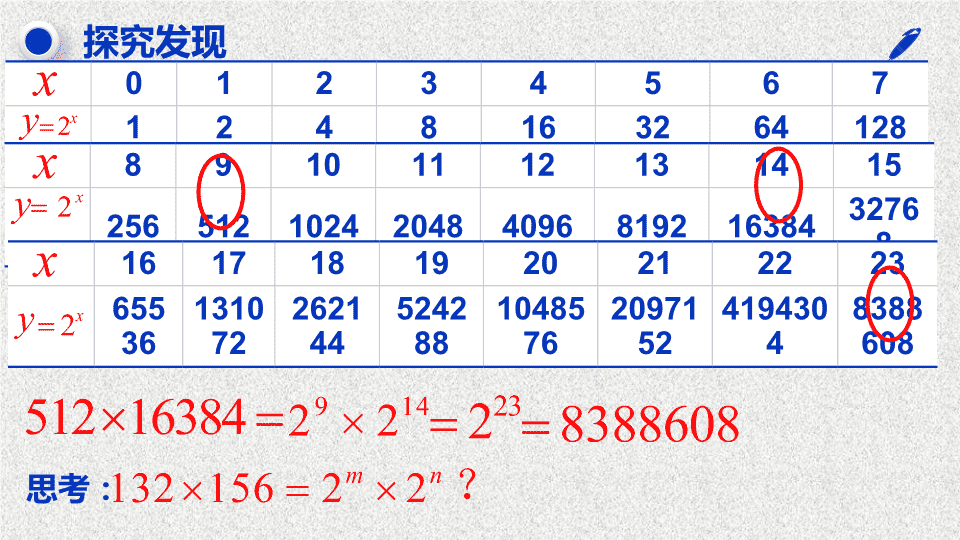
对数发明的背景 16 世纪,天文学蓬勃发展,天文学们每天都要面对大量繁琐的计算,特别是较大数的连乘,使他们苦不堪言。 探究发现 0 1 2 3 4 5 6 7 1 2 4 8 16 32 64 128 8 9 10 11 12 13 14 15 256 512 1024 2048 4096 8192 16384 32768 16 17 18 19 20 21 22 23 65536 131072 262144 524288 1048576 2097152 4194304 8388608 思考: 探究发现 前面,我们把 132 和 156 分别写成了 2 的乘幂的形式,即把 乘法运算转化成了乘幂运算 . 那么,更一般地: 给定正数 ,则 ,如何准确表示出 的值呢? 形成概念 观察数的运算的发展,思考问题: (1)已知 a + x = N ,求 x 引入减法 x = N - a ( 2 )已知 ax = N , 求 x 引入除法 ( 3 )已知 , 求 x 引入开方 ( 4 )已知 ,求 x 引入什么? 对数! 形成概念 对数: 一般地,如果 那么数 x 叫做以 a 为底 N 的 对数 , 其中 叫做对数的 底数 , 叫做对数的 真数 . 记作: 读作: 以 为底, 的对数 . 写作: 探究发现 0 1 2 3 4 5 6 7 1 2 4 8 16 32 64 128 8 9 10 11 12 13 14 15 256 512 1024 2048 4096 8192 16384 32768 16 17 18 19 20 21 22 23 65536 131072 262144 524288 1048576 2097152 4194304 8388608 概念生成 对数: 一般地,如果 那么数 x 叫做以 a 为底 的对数 , 记作 其中 叫做对数的底数, 叫做真数 . 意义: 对数表示一个数 ,相当于指数式中 的指数 . 指数式与对数式的互化 底数 底数 指数 对数 幂 真数 负数和零没有对数 例 1 将下列指(对)数式化成对(指)数式. 01 02 03 04 05 探究发现: 求下列各对数的值 . 01 03 02 04 “1” 的对数是 0. 底数的对数是 1 例 2 求下列各式中 x 的值 . 01 03 02 04 巩固练习一:求下列各式的值 01 0 3 0 2 0 4 0 5 0 6 1 提高训练 求值: 01 02 03 已 知 x 满足等式 , 求 的 值 . 求值 : 已知: ,求 的值 . 72 4 3 1 2 课堂小结 指数式和对数式的互化 常用的对数结论查看更多