黑龙江省实验校2020届高三第三次模拟考试数学（文）试题 Word版含解析

黑龙江省实验校2020届高三第三次模拟考试数学（文）试题 Word版含解析

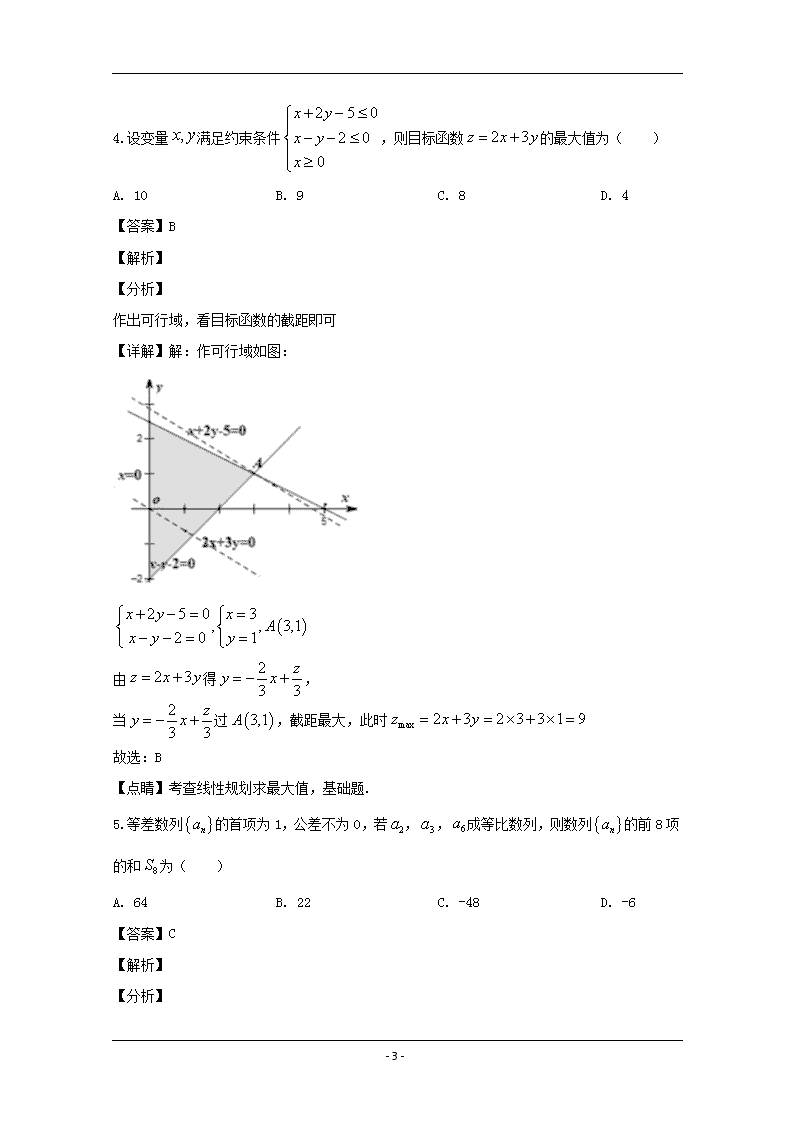
- 1 - 黑龙江省实验中学联盟校 2020 年高三第三次模拟考试 文科数学能力测试 考试时间：120 分钟 总分：150 分 注意事项： 1. 答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内. 2. 答题时请按要求用笔. 3. 请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草 稿纸、试卷上答题无效. 4. 作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑. 5. 保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀. 第Ⅰ卷（选择题，共 60 分） 一、选择题（本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一 项是符合题目要求的） 1.设集合  0,1A  ，  | ,B m m y x x A    且 y A ，则 A B  （ ） A.  B.  1 C.  0 D.  0,1 【答案】D 【解析】 【分析】 由题意首先求出集合 B，然后进行交集运算即可. 【详解】由 1−0=1, 0−1=−1, 1−1=0−0=0， 故由题意可知：  1,0,1B   ，结合交集的定义可知：  0,1A B  故选：D. 【点睛】本题主要考查集合的表示方法，交集的定义与运算等知识，意在考查学生的转化能 力和计算求解能力，属于基础题 . 2.已知复数 2 iz i    ，则 z在复平面上对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】C - 2 - 【解析】 【分析】 首先根据题意得到 1 2 5 5 z i   ，再求其点所对应的象限即可. 【详解】因为       2 1 2 1 2 2 2 2 5 5 5 i ii iz i i i i              ， 所以 z在复平面上对应的点为 1 2, 5 5       ，在第三象限. 故选：C 【点睛】本题主要考查复数的代数运算及几何意义，属于简单题. 3.已知向量 a  ，b  满足  1,1a  r ， 1b   ，且 2 2b a    ，则向量 a  与b  的夹角的余弦值为 （ ） A. 2 2 B. 2 3 C. 2 4 D. 2 5 【答案】A 【解析】 【分析】 先求出向量 a  的模，然后对 2 2b a    两边平方，得到向量的数量积，最后根据夹角公式 求解. 【详解】解：因为  1,1a  r ，所以 = 2a  ， 因为 2 2b a    ，所以 2 2 4 4 2b a b a        ，即 2 2 4 4 2b a b a        ， 因为 = 2a  ， 1b   ，所以 4 4 2 2a b      ，得 1a b    ， 设向量a  与b  的夹角为，则 1 2cos 22 a b a b          ， 故选：A 【点睛】此题考查平面向量的夹角的计算，属于基础题. 4.设变量 ,x y满足约束条件 2 5 0 2 0 0 x y x y x          ，则目标函数 2 3z x y  的最大值为（ ） - 3 - A. 10 B. 9 C. 8 D. 4 【答案】B 【解析】 【分析】 作出可行域，看目标函数的截距即可 【详解】解：作可行域如图：   2 5 0 3 , , 3,1 2 0 1 x y x A x y y            由 2 3z x y  得 2 3 3 zy x   ， 当 2 3 3 zy x   过  3,1A ，截距最大，此时 max 2 3 2 3 3 1 9z x y       故选：B 【点睛】考查线性规划求最大值，基础题. 5.等差数列 na 的首项为 1，公差不为 0，若 2a ， 3a ， 6a 成等比数列，则数列 na 的前 8项 的和 8S 为（ ） A. 64 B. 22 C. -48 D. -6 【答案】C 【解析】 【分析】 设公差为  0d d  ，运用等差数列的通项公式和等比数列的中项性质，解方程可得公差 d ， 再由等差数列的前 n项和公式，即可求出结果． - 4 - 【详解】等差数列 na 的首项为1，设公差 d （ 0d  ）． 若 2a ， 3a ， 6a 成等比数列， 所以 2 3 2 6a a a ，即      21 2 1 1 5d d d    ， 解得 2d   ， 所以 na 的前 8 项和为  8 8 78 1 2 48 2 S         ． 故选：C． 【点睛】本题主要考查了等差数列的通项公式和等差数列的前n项和公式，考查等比数列的中 项性质，考查方程思想和运算能力，属于基础题． 6.华罗庚是上世纪我国伟大的数学家，以华氏命名的数学科研成果有“华氏定理”、“华氏 不等式”、“华王方法”等.他除了数学理论研究，还在生产一线大力推广了“优选法”和 “统筹法”.“优选法”，是指研究如何用较少的试验次数，迅速找到最优方案的一种科学方 法.在当前防疫取得重要进展的时刻，为防范机场带来的境外输入，某机场海关在对入境人员 进行检测时采用了“优选法”提高检测效率：每 16 人为组，把每个人抽取的鼻咽拭子分泌物 混合检查，如果为阴性则全部放行；若为阳性，则对该 16 人再次抽检确认感染者.某组 16 人 中恰有一人感染（鼻咽拭子样本检验将会是阳性），若逐一检测可能需要 15 次才能确认感染 者.现在先把这 16 人均分为 2 组，选其中一组 8 人的样本混合检查，若为阴性则认定在另一 组；若为阳性，则认定在本组.继续把认定的这组的 8 人均分两组，选其中一组 4 人的样本混 合检查……以此类推，最终从这 16 人中认定那名感染者需要经过（ ）次检测. A. 3 B. 4 C. 6 D. 7 【答案】B 【解析】 【分析】 类比二分法，将 16 人均分为两组，选择其中一组进行检测，再把认定的这组的 8 人均分两组， 选择其中一组进行检测，以此类推，即可得解. 【详解】先把这 16 人均分为 2组，选其中一组 8 人的样本混合检查，若为阴性则认定在另一 组；若为阳性，则认定在本组，此时进行了 1次检测.继续把认定的这组的 8 人均分两组，选 其中一组 4 人的样本混合检查，为阴性则认定在另一组；若为阳性，则认定在本组，此时进 行了 2 次检测.继续把认定的这组的 4 人均分两组，选其中一组 2 人的样本混合检查，为阴性 则认定在另一组；若为阳性，则认定在本组，此时进行了 3次检测.选认定的这组的 2 人中一 - 5 - 人进行样本混合检查，为阴性则认定是另一个人；若为阳性，则认定为此人，此时进行了 4 次检测.所以，最终从这 16 人中认定那名感染者需要经过 4 次检测. 故选：B. 【点睛】本题考查的是二分法的实际应用，考查学生的逻辑推理能力，属于基础题. 7.已知函数   x xf x e e  ，  0.32a f ，  0.20.3b f ，  0.3log 2c f ，则 a，b，c 的大小关系为（ ） A. c b a  B. b a c  C. b c a  D. c a b  【答案】A 【解析】 【分析】 首先判断函数的单调性，再根据指数函数、对数函数的性质得到 0.32 1 ， 0.20 0.3 1  ， 0.3log 2 0 ，即可得解； 【详解】解：因为   x xf x e e  ，定义域为 R， xy e 在定义域上单调递增， xy e 在定义域上单调递减， 所以   x xf x e e  在定义域上单调递增， 由 0.32 1 ， 0.20 0.3 1  ， 0.3log 2 0 所以      0.3 0.2 0.32 0.3 log 2f f f  即c b a  故选：A 【点睛】本题考查指数函数、对数函数的性质的应用，属于基础题. 8.已知四棱锥 S ABCD 所有的棱都相等，过 BD与 SC 平行的平面与SA交于点 E，则 BE 与 CD所成角的大小是（ ） - 6 - A. 30° B. 45 C. 60 D. 90 【答案】A 【解析】 【分析】 要求异面直线 BE 与CD所成角，又 / /AB CD，根据异面直线所成的角的定义可知 ABE 就 是 BE 与CD所成角，而 / /SC 平面BDE，由线面平行的性质定理可得 //SC OE ，再结合O 是BD的中点，可得 E是SA的中点，在正 SAB 中即可求出 ABE 的大小. 【详解】设 AC BD O ，连接OE， 由 / /SC 平面 BDE， SC 平面 SAC，平面 SAC 平面 BDE OE ， 所以 //SC OE ，由O是 BD的中点，得E是SA的中点， 因为 / /AB CD，所以 ABE 就是 BE 与CD所成角， 因为 SAB 为正三角形，所以 30ABE   . 故选：A. 【点睛】本题主要考查求异面直线所成的角，同时考查线面平行的性质定理，属于中档题. 9.已知函数    sin sin 3 cosf x x x x  ，则下列说法正确的是（ ） - 7 - A.  f x 的最小正周期为2 B.  f x 关于点 ,0 12       对称 C.  f x 在 5, 3 6        上单调递减 D.  f x 的图象关于直线 6 x   对称 【答案】C 【解析】 【分析】 根据倍角公式和辅助角公式化简  f x ，得   1sin 2 6 2 f x x        ，求周期可直接判断 A 的正误；求 12 f       看是否为 1 2 ， 确定对称中心，判断 B 是否正确；求出2 6 x   的取值范围， 判断  f x 的单调性，判断 C 是否正确；把 6 x   代入  f x ，看  f x 是否取得最值，即得D 的正误. 【 详 解 】   2 1 cos 2 3 3 1 1sin 3 sin cos sin 2 sin 2 cos 2 2 2 2 2 2 xf x x x x x x x        1sin 2 6 2 x        . 对 A，  f x 的最小正周期为 ，故 A错误； 对 B， 1 1sin 2 12 12 6 2 2 f                  ，  f x 关于点 1, 12 2       对称，故 B错误； 对C，当 5 3 6 x       ， 时， 32 , 6 2 2 x         ， 又 siny t 在 3, 2 2 t       上单调递减，  f x 在 5 3 6        ， 上单调递减.故C正确； 对D， 1 1sin 2 sin 1 6 6 6 2 6 2 f                     ，不是最值，故D错误. 故选：C. 【点睛】本题考查三角恒等变换和三角函数的周期性，单调性，对称点，对称轴等性质，属 - 8 - 于中档题. 10.已知 A，B，C在球O的球面上， 3AC  ， 2BC  ， 30ACB  ，直线OA与截面 ABC所成的角为60，则球O的表面积为（ ） A. 4 B. 16 C. 4 3  D. 16 3  【答案】B 【解析】 【分析】 根据题中数量关系和余弦定理可证 ABC 为直角三角形，设BC的中点为 1O ，由球的性质可 知 1OO 平面 ABC，由线面角的概念可知 1 60OAO  ，在 1Rt AOOV 中可求出球O的半 径，由此即可求出结果. 【详解】由题意可知，在 ABC 中 3AC  ， 2BC  ， 30ACB  ， 由余弦定理可知， 2 2 2 2 cos 1AB AC BC A AC BC CB    ， 所以 2 2 2AB AC BC  ，所以 ABC 为直角三角形， 设BC的中点为 1O ，连接 1OO ， 如下图所示： 由题意可知 1OO 平面 ABC， 又直线OA与截面 ABC所成的角为60，所以 1 60OAO  ， 在 1Rt AOOV 中， 1 1O A  ，所以 1 2 cos60 OA    ，即球O的半径为 2， - 9 - 所以球O的表面积为 24 2 16   . 故选：B. 【点睛】本题考查的知识点是球的表面积，其中根据已知条件求出球的半径是解答本题的关 键． 11.已知点  3, 2M   ，抛物线 2 4x y ，F 为抛物线的焦点， l为抛物线的准线， P为抛物 线上一点，过 P作 PQ l ，点Q为垂足，过 P作 FQ的垂线 1l ，1l 与 l交于点 R，则 QR MR 的最小值为（ ） A. 1 13 B. 13 C. 10 D. 3 2 【答案】D 【解析】 【分析】 由题意画出图形，结合抛物线的定义，转化说明 QR MR 的最小值就是MF的距离的最小 值. 【详解】解：由题意可知 (0,1)F ，直线 l为 1y   ， 根据抛物线的定义可得 1 ,l FQPF PQ  ， 所以 1l 为 FQ的垂直平分线，所以 RF RQ , 所以 QR MR RF MR MF    ， 当且仅当 , ,M R F 三点共线取等号， 所以 QR MR 的最小值为 2 2( 3 0) ( 2 1) 18 3 2MF         故选：D - 10 - 【点睛】此题考查抛物线的简单性质的应用，考查数形结合以及转化思想计算能力，属于中 档题. 12.已知函数 11 2ln ,y x x e e          的图象上存在点M ，函数 2y x a   的图象上存在点 N ，且点M N， 关于原点对称，则实数 a的取值范围是（ ） A. 2 10,1 e     B. 20, 3e   C. 2 2 11 , 3e e      D. 2 11 , e     【答案】B 【解析】 【分析】 原题等价于函数 11 2ln ,y x x e e          的图象与函数 2y x a  的图象有交点，即方程 2 11 2ln ,x x a x e e           有 解 ， 即 2 11 2ln ,a x x x e e           有 解 ， 令   2 1 2lnf x x x   ，利用导数法求出函数的值域，即可求得答案 【详解】函数 2y x a   的图象与函数 2y x a  的图象关于原点对称， 则原题等价于函数 11 2ln ,y x x e e          的图象与函数 2y x a  的图象有交点， 即方程 2 11 2ln ,x x a x e e           有解， 即 2 11 2ln ,a x x x e e           有解， 令   2 11 2ln ,f x x x x e e           ， 则    22 122 x f x x x x      ， 当 1 ,1x e      时，   0f x  ， - 11 - 当  1,x e ，   0f x  ，故    min 1 0f x f  ， 由 2 1 1 1f e e        ，   2 3f e e  ， 故当 x e 时，   2 max 3f x e  故 a的取值范围为 20, 3e   . 故选：B. 【点睛】本题考查了图象的对称性，以及运用导数求函数的单调区间，极值的求解，在利用 导数求单调区间的过程中，要注意定义域的范围． 第Ⅱ卷（非选择题，共 90 分） 二、填空题（本大题共 4 小题，共 20 分） 13.若曲线 2 2lny x x  的一条切线的斜率是 3，则切点的横坐标为________． 【答案】2 【解析】 【分析】 根据曲线的切线斜率即对应的函数在切点处的导数值，令导数 22 3y x x     ，解得 x 的值， 结合函数定义域即可得解． 【详解】解： 2 2lny x x  ， 22 3y x x     ， 2 0 02 3 2 0x x   ，解得 0 1 2 x   （舍 去）或 0 2x  ， 所以 0 2x  ，故答案为 2. 【点睛】本题考查导数的几何意义，曲线上某点处的切线斜率的意义以及函数的定义域，属 于基础题. 14.2019 年 7 月 1，《上海市生活垃圾管理条例》正式实施，生活垃圾要按照“可回收物”、 “有害垃圾”、“湿垃圾”、“干垃圾”的分类标准进行分类，没有对垃圾分类或未投放到 指定垃圾桶内都会被处罚.若某上海居民提着厨房里产生的“湿垃圾”随意地投放到楼下的 “可回收物”、“有害垃圾、“湿垃圾”，“干垃圾”四个垃圾桶内，则该居民会被处罚的 概率为______. - 12 - 【答案】 3 4 【解析】 【分析】 由已知随意投放有 4 中，错误投放有 3 种，即可求解. 【详解】“湿垃圾”随意地投放到楼下的“可回收物”、“有害垃圾、 “湿垃圾”、“干垃圾”四个垃圾桶内，有 4 种投放方法， 被处罚的投放有“可回收物”、“有害垃圾、“干垃圾”3 种投法， 该居民会被处罚的概率为 3 4 . 故答案为: 3 4 . 【点睛】本题考查古典概型的概率，属于基础题. 15.已知双曲线   2 2 2 2 1 0, 0x y a b a b     的两条渐近线分别为直线 1l ， 2l ，经过右焦点 F 且垂 直于 1l 的直线 l分别交 1l ， 2l 于 A， B两点，且 2FB AF   ，则该双曲线的离心率为______. 【答案】 2 3 3 【解析】 【分析】 求出直线 l与渐近线的两个交点，根据向量关系得到 , ,a b c的一个等量关系，从而可求离心率. 【详解】双曲线的渐近线的方程为 by x a   . 不妨设直线 l的方程为  ay x c b    ， 由  ay x c b by x a         可得 2ax c aby c       ，所以 2 ,a abA c c       . - 13 - 由  ay x c b by x a          可得 2 2 2 2 2 a cx a b abcy a b          ，所以 2 2 2 2 2,a c abcB a b a b       ， 因为 2FB AF   ，故 2 2 2 2 2 2 2 0 2 0 a c ac c a b c abc ab a b c                     ， 整理得到 2 2 22 2c a b  即 2 23 4c a ，故 2 3 3 e  ， 故答案为： 2 3 3 . 【点睛】本题考查双曲线的离心率，此类问题，一般是寻找 , ,a b c的一个等量关系即可，关系 的构建依靠坐标关系或几何关系. 16.纸张的规格是指纸张制成后，经过修整切边，裁成一定的尺寸.现在我国采用国际标准， 规定以 AO、 1A 、 2A 、 1B 、 2B 、…等标记来表示纸张的幅面规格.复印纸幅面规格只采 用 A系列和 B系列，其中  , 8nA n N n  系列的幅面规格为：① AO、 1A 、 2A 、…、 8A 所有规格的纸张的幅宽（以 x表示）和长度（以 y表示）的比例关系都为 : 1: 2x y  ；②将 AO纸张沿长度方向对开成两等分，便成为 1A 规格， 1A 纸张沿长度方向对开成两等分，便 成为 2A 规格，…，如此对开至 8A 规格.现有 AO、 1A 、 2A 、…、 8A 纸各一张.若 4A 纸 的宽度为 2dm，则 1A 纸的长度为______dm； 1A 、 2A 、…、 8A 八张纸的面积之和等于 ______ 2dm . 【答案】 (1). 8 (2). 255 2 4 【解析】 【分析】 可设  0,1,2,3, ,8iA i   的纸张的长度为 1ia  ，则数列 na 成以 2 2 为公比的等比数列，设 iA的纸张的面积 1iS  ，则数列 nS 成以 1 2 为公比的等比数列，然后利用等比数列的通项公式 - 14 - 求出数列 nS 的首项，并利用等比数列的求和公式求出答案. 【详解】可设  0,1,2,3, ,8Ai i   的纸张的长度为 1ia  ，面积为 1iS  ， 1iA  的长度为 2 1 2 2i ia a  ，所以数列 na 是以 2 2 为公比的等比数列， 4A 纸的宽度为2dm，则， 4A 纸的长度为 5 2 2a  dm 所以 1A 纸的长度为 5 2 3 3 2 2 8 2 2 2 2 aa                所以， 1A 纸的面积为 2 2 2 2 2 2 2 8 32 2 2 2 S a dm    ， 又 22 2n nS a ， 2 22 1 1 1 2 2 2 12 2 22 2 n n n n n n aS a S a a                   ， 所以，数列 nS 是以 32 2 为首项，以 1 2 为公比的等比数列， 因此，这 8 张纸的面积之和等于 8 2 132 2 1 255 22 1 41 2 dm         . 故答案为：8； 255 2 4 . 【点睛】本题考查数列应用题的解法，考查等比数列通项公式与求和公式的应用，考查运算 求解能力，属于中等题. 三、解答题（共 70 分.解答应写出必要的文字说明，证明过程或演算步骤.第 17-21 题为必考 题，每个试题考生都必须作答.第 22、23 题为选考题，考生根据要求作答） （一）必考题（60 分） 17.如图，在四棱锥 P ABCD 中， PD 平面 ABCD， / /CD AB， 2AD CD BC   ， 4AB  . - 15 - （1）求证:平面 PAD 平面 PBD； （2）若三棱锥C PBD 的体积为 3，求 PB的长. 【答案】（1）证明见解析（2） 21 【解析】 【分析】 （1）过点D作 DE AB 于点E .由已知可以证明出四边形 ABCD是等腰梯形，利用勾股定理 的逆定理通过计算可以证明出BD AD ，结合已知的线面垂直关系，可以得到 BD PD ， 这样通过线面垂直的判定定理和面面垂直的判断定理证明即可； （2）利用三棱锥的体积公式和三棱锥的体积性质进行求解即可. 【详解】（1）证明：如图，过点D作DE AB 于点 E .因为 / / , 2, 4CD AB AD CD BC AB    ，所以四边形 ABCD是等腰梯形，可得 1, 3, 3, 2 3AE BE DE BD    ，所以 2 2 2AB AD BD  ，所以BD AD .又因为 PD 平面 ,ABCD BD 平面 ABCD，所以 BD PD .因为 , ,AD PD D PD AD   平 面PAD，所以BD 平面 PAD .因为 BD 平面 PBD，所以平面 PAD 平面 PBD . - 16 - （2） 1 2 3 3 2BCDS    △ .因为三棱锥C PBD 的体积为 3，所以 1 1 3 3 3 3C PBD P BCD BCDV V S PD PD        △ 解得 3PD  .在 Rt PDB△ 中， 2 3, 3BD PD  ，所以 2 2 2 2(2 3) 3 21PB BD PD     . 【点睛】本题考查了利用面面垂直的判定定理证明面面垂直，考查了三棱锥体积公式的应用， 考查了推理论证能力和数学运算能力. 18.在 ABC 中，角 A， B，C的对边分别为 a，b， c， (sin sin )( ) (sin sin )A B a b c C B    . （1）求 A； （2）若 2 2a b c  ，求 sinC . 【答案】（1） 3 A   ；（2） 6 2sin 4 C   . 【解析】 【分析】 （1）利用正弦定理角化边，利用余弦定理求角 A； （2）由 2 2a b c  用正弦定理化为角的关系，由 3 A   ， 2 3 B C    ，转化为只含角C的 方程，化简求出角C，求出sinC . 【详解】（1）∵ (sin sin )( ) (sin sin )A B a b c C B    ， ∴由正弦定理可得：     a b a b c c b    ，即： 2 2 2b c a bc   ， 由余弦定理得 2 2 2 1cos 2 2 b c aA bc     ，∵  0,A  ，∴ 3 A   . （2）∵ 2 2a b c  ，由正弦定理得： 2 sin sin 2 sinA B C  ， 又  sin sin sin cos cos sinB A C A C A C    ， 3 A   ， ∴ 3 3 12 cos sin 2sin 2 2 2 C C C    ， 整理可得：3sin 6 3cosC C  ，即3sin 3cos 2 3sin 6 6 C C C         ， - 17 - ∴ 2sin 6 2 C       ，由 20, 3 C      ， , 6 6 2 C          ， 所以 6 4 C     ， 4 6 C     ， 2 3 2 1 6 2sin sin 4 6 2 2 2 2 4 C              . 【点睛】本题考查了正弦定理、余弦定理，两角和差公式，辅助角公式，还考查了分析推理 能力，运算能力，属于中档题. 19.某生活超市有一专柜预代理销售甲乙两家公司的一种可相互替代的日常生活用品．经过一 段时间分别单独试销甲乙两家公司的商品，从销售数据中随机各抽取 50 天，统计每日的销售 数量，得到如下的频数分布条形图．甲乙两家公司给该超市的日利润方案为：甲公司给超市 每天基本费用为 90 元，另外每销售一件提成 1元；乙公司给超市每天的基本费用为 130 元， 每日销售数量不超过 83 件没有提成，超过 83 件的部分每件提成 10 元． （Ⅰ）求乙公司给超市的日利润 y（单位：元）与日销售数量 n的函数关系； （Ⅱ）若将频率视为概率，回答下列问题： （1）求甲公司产品销售数量不超过 87 件的概率； （2）如果仅从日均利润的角度考虑，请你利用所学过的统计学知识为超市作出抉择，选择哪 家公司的产品进行销售？并说明理由． 【答案】（Ⅰ） 130,0 83 10 700, 83 n y n n       ；（Ⅱ）（1） 2 5 ；（2）超市应代理销售乙公司的产品较 为合适． 【解析】 【分析】 - 18 - （Ⅰ）分别在0 83n  和 83n  两种情况下得到关系式，进而得到结果； （Ⅱ）（1）利用频率的计算方式可求得对应的概率； （2）分别计算甲、乙两公司给到超市的日利润的平均数，选择平均数较大的产品进行销售. 【详解】（Ⅰ）当0 83n  时， 130y  元； 当 83n  时，  130 83 10 10 700y n n      ； 乙公司给超市的日利润 y（单位：元）与销售数量n的函数关系为： 130,0 83 10 700, 83 n y n n       . （Ⅱ）（1）记事件 A：“甲公司产品的销售数量不超过 87 件”， 则   5 10 5 2 50 5 P A     ； （2）甲公司给超市的日利润为 X 元， 则 X 的所有可能取值为171，174，177，180，183，  1 171 5 174 10 177 5 180 20 183 10 178.2 50 X             （元）； 设乙公司给超市的日利润为Y 元， 则Y 的所有可能取值为130，140，170， 200， 230， 则  1 130 50 0 5 10 5 40 10 70 15 100 15 190 50 Y               （元）； X Y ，所以超市应代理销售乙公司的产品较为合适． 【点睛】本题考查函数关系式的求解、利用频数条形图计算频率、频数条形图的实际应用问 题；关键是能够准确读懂频数条形图，属于基础题型. 20.已知椭圆C：   2 2 2 2 1 0x y a b a b     的上顶点为M ，左，右焦点分别为 1F， 2F ， 1 2MFF△ 的面积为 3，直线 1FM 的斜率为 3 .O为坐标原点. （1）求椭圆C的方程； （2）设过点  2,0A 的直线 l与椭圆C交于点 B（ B不在 x轴上），垂直于 l的直线与 l交于点 P，与 y轴交于点Q . 2 2 0BF QF    ，且 POA PAO   ，求直线 l的方程. 【答案】（1） 2 2 1 4 3 x y   ；（2） 6 ( 2) 4 y x   . 【解析】 - 19 - 【分析】 （1）由 1 2MFF△ 的面积为 3可得， 1 2 3 2 c b   ，由直线 1FM 的斜率为 3，有 3b c  ， 再根据 2 2 2a b c  ，可解得 ,a b的值，得到椭圆方程. （2）设直线 l的方程为    2 0y k x k   ，  ,B BB x y ，将直线 l的方程与椭圆方程联立解 出点 B坐标，由 2 2 0BF QF    ，得出点Q坐标，再由 POA PAO   ，得 P为OA的垂直平 分线与 l的交点，所以  1,P k ，根据由 PQ l 得出斜率 k的值,从而得出直线方程. 【详解】（1）因为 1 2MFF△ 的面积为 3，所以 1 2 3 2 c b   由直线 1FM 的斜率为 3 ,则 3b c  ，又 2 2 2a b c  ， 所以 2 4a  ， 2 3b  ，故椭圆方程为 2 2 1 4 3 x y   . （2）设直线 l的方程为    2 0y k x k   ，  ,B BB x y ， 由 2 23 4 12 2 0 x y kx y k         ，可得  2 2 2 24 3 16 16 12 0k x k x k     ， 解得 2x  或 2 2 8 6 4 3B kx k    ，所以 2 12 4 3B ky k    ， 2 2 2 8 6 12, 4 3 4 3 k kB k k        ， 设  0, QQ y ，有  2 1, QF Q y   ， 2 2 2 2 9 4 12, 4 3 4 3 k kBF k k         ， 由 2 2BF QF ，得 2 2 0BF QF    ， 所以 2 2 2 124 9 0 4 3 4 3 Qkyk k k      ，解得 29 4 12Q ky k   ， 由 POA PAO   ，得 P为OA的垂直平分线与 l的交点，所以  1,P k ， 由PQ l ，得 29 4 12 1 1 k k k k       ， 得 2 3 8 k  ，解得 6 4 k   ， - 20 - 所以，直线 l的方程为 6 ( 2) 4 y x   . 【点睛】本题考查根据条件求椭圆的方程，考查方程联立求点的坐标，根据直线的垂直关系 求解直线的方程，考查运算能力，属于中档题. 21.已知函数 ( 1)(1 )( ) 2 ln x mxf x x x     ． （Ⅰ）当 1m  时，试判断 ( )f x 零点的个数； （Ⅱ）若 1x  时， ( ) 0f x  ，求m的取值范围． 【答案】（Ⅰ）  f x 有且只有一个零点；（Ⅱ）[1, ) ． 【解析】 【分析】 （Ⅰ）求导数判断函数的单调性及 (1) 0f  即可确定函数的零点； （Ⅱ）分 0m  和 0m  两种情况，分别判断函数的单调性，根据单调性求函数  f x 的最大 值，由 max( ) 0f x  求解即可． 【详解】（Ⅰ）当 1 m  时， ( 1)(1 )( ) 2ln x xf x x x     ， 2 2 ( 1)( ) xf x x    ． 所以   0f x  ，  f x 在 (0, ) 上单调递减， 又 (1) 0f  ， ∴  f x 有且只有一个零点． （Ⅱ）∵  1 0f  ， 2 2 2 1( ) mx xf x x     ． - 21 - （1）当 0m  时，在[1, ) 上 ( ) 0f x  恒成立， ∴ ( )f x 在[1, ) 上单调递增， ∴ ( ) (1) 0f x f  ，不符合题意． （2）当 0m  时，设 2( ) 2 1g x mx x    ， 当 4 4 0m    即m 1 时， 2( ) 2 1 0g x mx x     恒成立， 所以在[1, ) 上 ( ) 0f x  恒成立， ∴ ( )f x 在[1, ) 上单调递减， ∴ ( ) (1) 0f x f  ，符合题意， ∴m 1 ． 当 4 4 0m    即0 1m  时， ( ) 0g x  有两不等实根，设为 1 2,x x 因为 (1) 1 0g m   ，可知 1 21x x< < ， 所以  21,x x 时 ( ) 0f x  ，  2 ,x x  时 ( ) 0f x  即 ( )f x 在区间  21, x 上单调递增，  2 ,x  单调递减 所以  2 (1) 0f x f  ，不符合题意． 综上，m的取值范围为[1, ) ． 【点睛】本题主要考查了利用导数研究函数的单调性，零点，最值，不等式恒成立问题，属 于中档题. （二）选考题：共 10 分，请考生在第 22、23 题中任选一题作答，如果多做则按所做的第一 题计分. （选修 4-4：极坐标与参数方程） 22.在直角坐标系 xOy中，曲线 1C 的参数方程为 cos 3 sin 3 x y       （为参数）.圆 2C 的方程为  2 21 1x y   ，以原点O为极点， x轴的非负半轴为极轴且取相等的长度单位建立极坐标 系，射线 l的极坐标方程为 0 ( 0)    . （1）求曲线 1C 和 2C 的极坐标方程； - 22 - （2）当 00 2   时，若射线 l与曲线 1C 和圆 2C 分别交于异于点O的M 、 N 两点，且 2ON OM ，求 2MC N 的面积. 【答案】（1） 2 2 1 cos 3sin      ， 2cos  ；（2） 1 4 . 【解析】 【分析】 （1）先将曲线 1C 的参数方程化为普通方程，再表示成极坐标方程即得，由 cosx   ， siny   代入圆 2C 的普通方程，整理即得极坐标方程； （2）利用极径的几何意义和三角形的面积公式可得。 【详解】（1）∵曲线 1C 的普通方程为： 2 2 11 3 yx   ， 又 cosx   ， siny   代入：∴ 2 2 2 2cos 3 sin 1     ， ∴曲线 1C 的极坐标方程： 2 2 1 cos 3sin      ， ∴曲线 2C 的极坐标方程： 2cos  . （2）∵已知 2ON OM ，∴ 2 24N M  ， 2 2 2 14cos 4 cos 3sin      ， 4 22cos 3cos 1 0    ，且 00 2   ， ∴解得： 2 1cos 2   ， 2cos 2   ， 2sin 2   . 点 2C 到 l的距离 2 2 2 2sin 1 2 2Ch OC      . ∴ 2MC N 的面积为：   2 2 2 1 1 2 2NC M C N M CS NM h h       △ 22 2 1 1 12cos 2 4cos 3sin Ch            . 【点睛】本题考查参数方程，普通方程和极坐标方程间的互化，通过极径的几何意义最终求 三角形面积，属于中档题. - 23 - （选修 4-5：不等式选讲） 23.已知函数   2 1 3 1f x x a x    . （1）当 1a  时，解不等式   3f x   ； （2）若   3 4f x a x  ，求 a的最小值. 【答案】（1） | 1 5x x   ；（2） 1 3 . 【解析】 【分析】 （1）当 1a  时，分三种情况去绝对值化简，得到分段函数 12, 3 1 1( ) 5 , 2 3 12, 2 x x f x x x x x              ，然后根 据 ( )f x 的单调性及 ( 1) (5) 3f f    ，即可得到本题答案； （2）由题，得 2 1 3 1 3 4 x a x x      ，又根据绝对值三角不等式，可得 2 1 1 3 1 3 4 3 x x x      ， 由此即可得到本题答案. 【详解】解：（1）当 1a  时， 12, 3 1 1( ) 5 , 2 3 12, 2 x x f x x x x x              ， 由 ( )f x 的单调性及 ( 1) (5) 3f f    ，得   3f x   的解集为 | 1 5x x   ； （2）由   3 4f x a x  ，得 2 1 3 1 3 4 x a x x      ， 因为 3 1 3 4 3 2 1x x x     ，所以 2 1 1 3 1 3 4 3 x x x      ， 得 1 3 a  （当且仅当 1 3 x  或 4 3 x   时等号成立）， - 24 - 故 a的最小值为 1 3 . 【点睛】本题主要考查 +x a x b c   型不等式的解法，以及利用绝对值三角不等式确定 参数的取值范围，考查学生的转化求解能力和运算能力. - 25 -