2020届二轮复习平面向量位置关系问题的解法教案（全国通用）

2020届二轮复习平面向量位置关系问题的解法教案（全国通用）

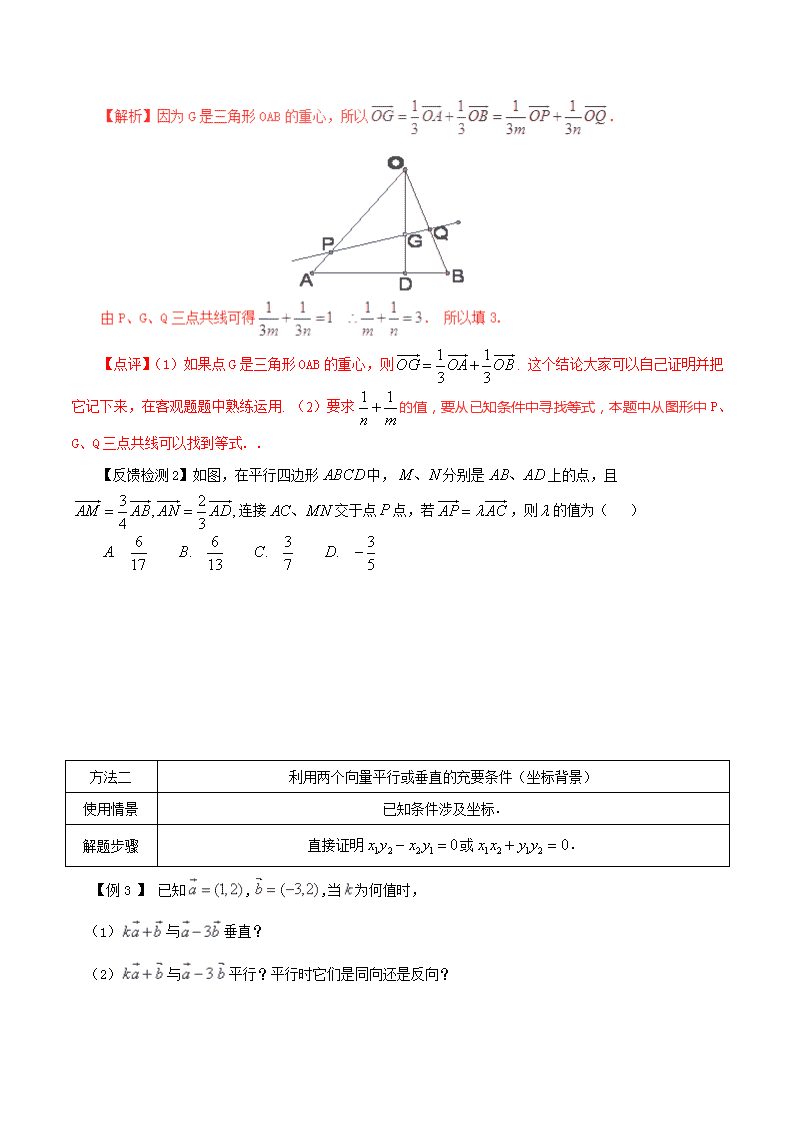
‎【例1】 设两非零向量和不共线，如果＝＋，＝3（－），，求证：三点共线.‎ ‎【点评】向量里证明三点共线一般分两步证明：（1）先证明(或)；(2)说明两个向量有公共点.其中第二步是不能省略的，因为只能说明平行或重合.所以必须加上第2步才能说明它们三点共线.‎ ‎【反馈检测1】设、是两个不共线的非零向量（）‎ ‎ （1）记那么当实数t为何值时，三点共线？‎ ‎（2）若，那么实数为何值时的值最小？‎ ‎【例2】已知PQ过三角形OAB的重心G，且P、Q分别在OA、OB上，设 则的值为 .‎ ‎【点评】（1）如果点G是三角形OAB的重心，则. 这个结论大家可以自己证明并把它记下来，在客观题题中熟练运用. （2）要求的值，要从已知条件中寻找等式，本题中从图形中P、G、Q三点共线可以找到等式. .‎ ‎【反馈检测2】如图，在平行四边形中，分别是上的点，且 连接交于点点，若，则的值为（ ）‎ 方法二 利用两个向量平行或垂直的充要条件（坐标背景）‎ 使用情景 已知条件涉及坐标.‎ 解题步骤 直接证明或.‎ ‎【例3 】 已知,,当为何值时，‎ ‎（1）与垂直？‎ ‎（2）与平行？平行时它们是同向还是反向？‎ ‎【点评】（1）如果=,=，则|| 和是判定平面向量位置关系的两个重要结论.（2）如果，则当时，两个向量同向，当时，两个向量方向相反.‎ ‎【反馈检测3】已知向量.‎ ‎(1)若点不能构成三角形，求实数应满足的条件；‎ ‎(2)若为直角三角形，求实数的值．‎ 高中数常见题型解法归纳及反馈检测第45讲:‎ 平面向量位置关系问题的解法参考答案 ‎【反馈检测1答案】（1）证明见后面解析；（2）‎ ‎【反馈检测2答案】A ‎【反馈检测2详细解析】‎ 因为三点共线，所以 ‎【反馈检测3答案】（1）；（2）或或.‎ ‎【反馈检测3详细解析】　(1) 已知向量.‎ 若点不能构成三角形，则这三点共线，‎ ‎∵，，故知，∴实数时，满足条件．‎ ‎(2)由题意，为直角三角形，‎ ‎①若为直角，则， ∴，解得.‎ ‎②若为直角，，则，∴，解得 ‎③若为直角，则，∴，解得.‎ 综上，或或.‎ ‎ ‎