2011年数学理（山东）高考试题

2011年数学理（山东）高考试题

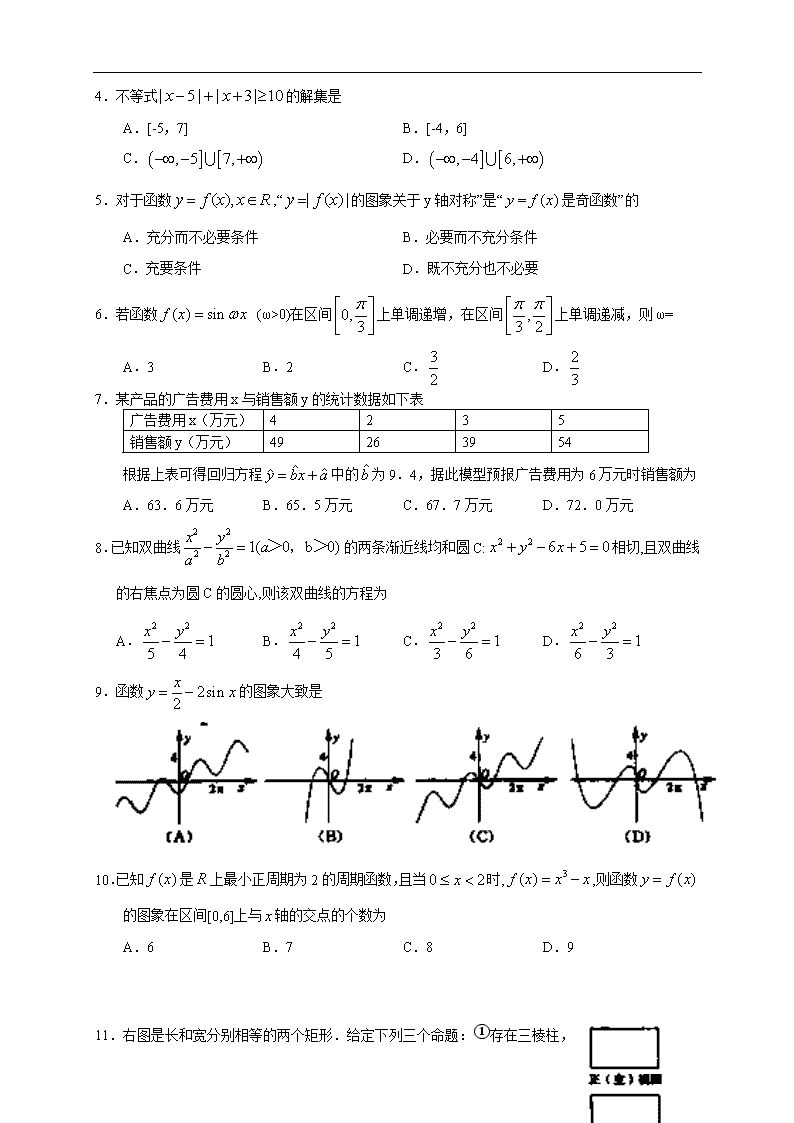
‎2011年普通高等学校招生全国统一考试（山东卷）‎ 理科数学 ‎ 本试卷分第I卷和第II卷两部分，共4页，满分150分。考试用时120分钟，考试结束后，将 本试卷和答题卡一并交回。‎ 注意事项：‎ ‎1．答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证证、县区和科类填写在答题卡和试卷规定的位置上。‎ ‎2．第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上。‎ ‎3．第II卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。不按能上能下要求作答的答案无效。‎ ‎4．填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。‎ 参考公式：‎ 柱体的体积公式：，其中S是柱体的底面积，h是柱体的高。‎ 圆柱的侧面积公式：，其中c是圆柱的底面周长，是圆柱的母线长。‎ 球的体积公式：，其中R是球的半径。‎ 球的表面积公式：，其中R是球的半径。‎ 用最小二乘法求线性回归方程系数公式：，‎ 如果事件A、B互斥，那么P（A+B）=P（A）+P（B）‎ 第Ⅰ卷（共60分）‎ 一、选择题：本大题共l0小题．每小题5分，共50分在每小题给出的四个选项中，只有一项是满足题目要求的．‎ ‎1．设集合 M ={x|}，N ={x|1≤x≤3},则M∩N =‎ ‎ A．[1,2） B．[1,2] C．（ 2,3] D．[2,3]‎ ‎2．复数z=（为虚数单位）在复平面内对应的点所在象限为 ‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3．若点（a,9）在函数的图象上，则tan=的值为 ‎ A．0 B． C．1 D．‎ ‎4．不等式的解集是 ‎ ‎ A．[-5，7] B．[-4，6] ‎ ‎ C． D．‎ ‎5．对于函数,“的图象关于y轴对称”是“=是奇函数”的 ‎ A．充分而不必要条件 B．必要而不充分条件 ‎ ‎ C．充要条件 D．既不充分也不必要 ‎6．若函数 (ω>0)在区间上单调递增，在区间上单调递减，则ω=‎ ‎ A．3 B．‎2 ‎ C． D．‎ ‎7．某产品的广告费用x与销售额y的统计数据如下表 广告费用x（万元）‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y（万元）‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程中的为9．4，据此模型预报广告费用为6万元时销售额为 ‎ A．63．6万元 B．65．5万元 C．67．7万元 D．72．0万元 ‎8．已知双曲线的两条渐近线均和圆C:相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为 A． B． C． D．‎ ‎9．函数的图象大致是 ‎10．已知是上最小正周期为2的周期函数，且当时,,则函数的图象在区间[0,6]上与轴的交点的个数为 A．6 B．‎7 ‎ C．8 D．9‎ ‎11．右图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，‎ 其正（主）视图、俯视图如下图；②存在四棱柱，其正（主）视图、俯 视图如右图；③存在圆柱，其正（主）视图、俯视图如右图．其中真命 题的个数是 ‎ A．3 B．2 ‎ ‎ C．1 D．0‎ ‎12．设，，，是平面直角坐标系中两两不同的四点，若 （λ∈R），（μ∈R），且,则称，调和分割， ,已知平面上的点C，D调和分割点A，B则下面说法正确的是 ‎ A．C可能是线段AB的中点 ‎ ‎ B．D可能是线段AB的中点 ‎ C．C，D可能同时在线段AB上 ‎ ‎ D．C，D不可能同时在线段AB的延长线上 第II卷（共90分）‎ 二、填空题：本大题共4小题，每小题4分，共16分．‎ ‎13．执行右图所示的程序框图，输入l=2，m=3，n=5，则输出的y的值是 ‎ ‎14．若展开式的常数项为60，则常数的值为 .‎ ‎15．设函数,观察:‎ 根据以上事实，由归纳推理可得：‎ 当且时， .‎ ‎16．已知函数=当2＜a＜3＜b＜4时，函数的零点 .‎ 三、解答题：本大题共6小题，共74分．‎ ‎17．（本小题满分12分）‎ 在ABC中，内角A，B，C的对边分别为a，b，c．已知．‎ ‎ （I）求的值；‎ ‎ （II）若cosB=，b=2，的面积S。‎ ‎18．（本小题满分12分）‎ 红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛，甲对A，乙对B，丙对C各一盘，已知甲胜A，乙胜B，丙胜C的概率分别为0.6,0.5,0.5，假设各盘比赛结果相互独立。‎ ‎（Ⅰ）求红队至少两名队员获胜的概率；‎ ‎（Ⅱ）用表示红队队员获胜的总盘数，求的分布列和数学期望.‎ ‎19．（本小题满分12分）‎ 在如图所示的几何体中，四边形ABCD为平行四边形，∠ ACB=，ＥＡ⊥平面ＡＢＣＤ，EF∥ＡＢ，ＦＧ∥ＢＣ，ＥＧ∥ＡＣ.ＡＢ=２ＥＦ.‎ ‎（Ⅰ）若Ｍ是线段ＡＤ的中点，求证：ＧＭ∥平面ＡＢＦＥ;‎ ‎（Ⅱ）若ＡＣ＝ＢＣ=２ＡＥ,求二面角Ａ-ＢＦ-Ｃ的大小．‎ ‎20．（本小题满分12分）‎ 等比数列中，分别是下表第一、二、三行中的某一个数，且 中的任何两个数不在下表的同一列．‎ 第一列 第二列 第三列 第一行 ‎3‎ ‎2‎ ‎10‎ 第二行 ‎6‎ ‎4‎ ‎14‎ 第三行 ‎9‎ ‎8‎ ‎18‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若数列满足：，求数列的前n项和．‎ ‎21．（本小题满分12分）‎ 某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为立方米，且．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为千元，设该容器的建造费用为千元．‎ ‎（Ⅰ）写出关于的函数表达式，并求该函数的定义域；‎ ‎（Ⅱ）求该容器的建造费用最小时的．‎ ‎22．（本小题满分14分）‎ 已知动直线与椭圆C: 交于P、Q两不同点，且△OPQ的面积=,其中O为坐标原点.‎ ‎（Ⅰ）证明和均为定值;‎ ‎（Ⅱ）设线段PQ的中点为M，求的最大值；‎ ‎（Ⅲ）椭圆C上是否存在点D,E,G，使得?若存在，判断△DEG的形状；若不存在，请说明理由.‎ 参考答案 一、选择题 ADDDBCBACBAD 二、填空题 ‎13．68 14．4 15． 16．2‎ 三、解答题 ‎17．解：‎ ‎ （I）由正弦定理，设 则 所以 即，‎ 化简可得 又，‎ 所以 因此 ‎ （II）由得 由余弦定理 解得a=1。‎ 因此c=2‎ 又因为 所以 因此 ‎18．解：（I）设甲胜A的事件为D，‎ 乙胜B的事件为E，丙胜C的事件为F，‎ 则分别表示甲不胜A、乙不胜B，丙不胜C的事件。‎ 因为 由对立事件的概率公式知 红队至少两人获胜的事件有：‎ 由于以上四个事件两两互斥且各盘比赛的结果相互独立，‎ 因此红队至少两人获胜的概率为 ‎ （II）由题意知可能的取值为0，1，2，3。‎ 又由（I）知是两两互斥事件，‎ 且各盘比赛的结果相互独立，‎ 因此 由对立事件的概率公式得 所以的分布列为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎0．1‎ ‎0．35‎ ‎0．4‎ ‎0．15‎ 因此 ‎19．（I）证法一：‎ 因为EF//AB，FG//BC，EG//AC，，‎ 所以∽‎ 由于AB=2EF，‎ 因此，BC=2FC，‎ 连接AF，由于FG//BC，‎ 在中，M是线段AD的中点，‎ 则AM//BC，且 因此FG//AM且FG=AM，‎ 所以四边形AFGM为平行四边形，‎ 因此GM//FA。‎ 又平面ABFE，平面ABFE，‎ 所以GM//平面AB。‎ 证法二：‎ 因为EF//AB，FG//BC，EG//AC，，‎ 所以∽‎ 由于AB=2EF，‎ 因此，BC=2FC，‎ 取BC的中点N，连接GN，‎ 因此四边形BNGF为平行四边形，‎ 所以GN//FB，‎ 在中，M是线段AD的中点，连接MN，‎ 则MN//AB，‎ 因为 所以平面GMN//平面ABFE。‎ 又平面GMN，‎ 所以GM//平面ABFE。‎ ‎ （II）解法一：‎ 因为，‎ 又平面ABCD，‎ 所以AC，AD，AE两两垂直，‎ 分别以AC，AD，AE所在直线为x轴、y轴和z轴，建立如图所法的空间直角坐标系，‎ 不妨设 则由题意得A（0，0，0，），B（2，-2，0），C（2，0，0，），E（0，0，1），‎ 所以 又 所以 设平面BFC的法向量为 则 所以取 所以 设平面ABF的法向量为，‎ 则 所以 则，‎ 所以 因此二面角A—BF—C的大小为 解法二：‎ 由题意知，平面平面ABCD，‎ 取AB的中点H，连接CH，‎ 因为AC=BC，‎ 所以，‎ 则平面ABFE，‎ 过H向BF引垂线交BF于R，连接CR，‎ 则 所以为二面角A—BF—C的平面角。‎ 由题意，不妨设AC=BC=2AE=2。‎ 在直角梯形ABFE中，连接FH，‎ 则，又 所以 因此在中，‎ 由于 所以在中，‎ 因此二面角A—BF—C的大小为 ‎20．解：（I）当时，不合题意；‎ 当时，当且仅当时，符合题意；‎ 当时，不合题意。‎ 因此 所以公式q=3，‎ 故 ‎ （II）因为 所以 ‎ 所以 当n为偶数时，‎ 当n为奇数时，‎ 综上所述，‎ ‎21．解：（I）设容器的容积为V，‎ 由题意知 故 由于 因此 所以建造费用 因此 ‎ （II）由（I）得 由于 当 令 所以 ‎ （1）当时，‎ 所以是函数y的极小值点，也是最小值点。‎ ‎ （2）当即时，‎ 当函数单调递减，‎ 所以r=2是函数y的最小值点，‎ 综上所述，当时，建造费用最小时 当时，建造费用最小时 ‎22．（I）解：（1）当直线的斜率不存在时，P，Q两点关于x轴对称，‎ 所以 因为在椭圆上，‎ 因此 ①‎ 又因为 所以 ②‎ 由①、②得 此时 ‎ （2）当直线的斜率存在时，设直线的方程为 由题意知m，将其代入，得 ‎，‎ 其中 即 …………（*）‎ 又 所以 因为点O到直线的距离为 所以 又 整理得且符合（*）式，‎ 此时 综上所述，结论成立。‎ ‎ （II）解法一：‎ ‎ （1）当直线的斜率存在时，‎ 由（I）知 因此 ‎ （2）当直线的斜率存在时，由（I）知 所以 ‎ ‎ 所以，当且仅当时，等号成立.‎ 综合（1）（2）得|OM|·|PQ|的最大值为 解法二：‎ 因为 ‎ ‎ 所以 即当且仅当时等号成立。‎ 因此 |OM|·|PQ|的最大值为 ‎ （III）椭圆C上不存在三点D，E，G，使得 证明：假设存在，‎ 由（I）得 因此D，E，G只能在这四点中选取三个不同点，‎ 而这三点的两两连线中必有一条过原点，‎ 与矛盾，‎ 所以椭圆C上不存在满足条件的三点D，E，G.‎