- 2021-06-16 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
山西省太原市第五中学2020届高三数学(理)6月模拟考试试题(Word版附答案)
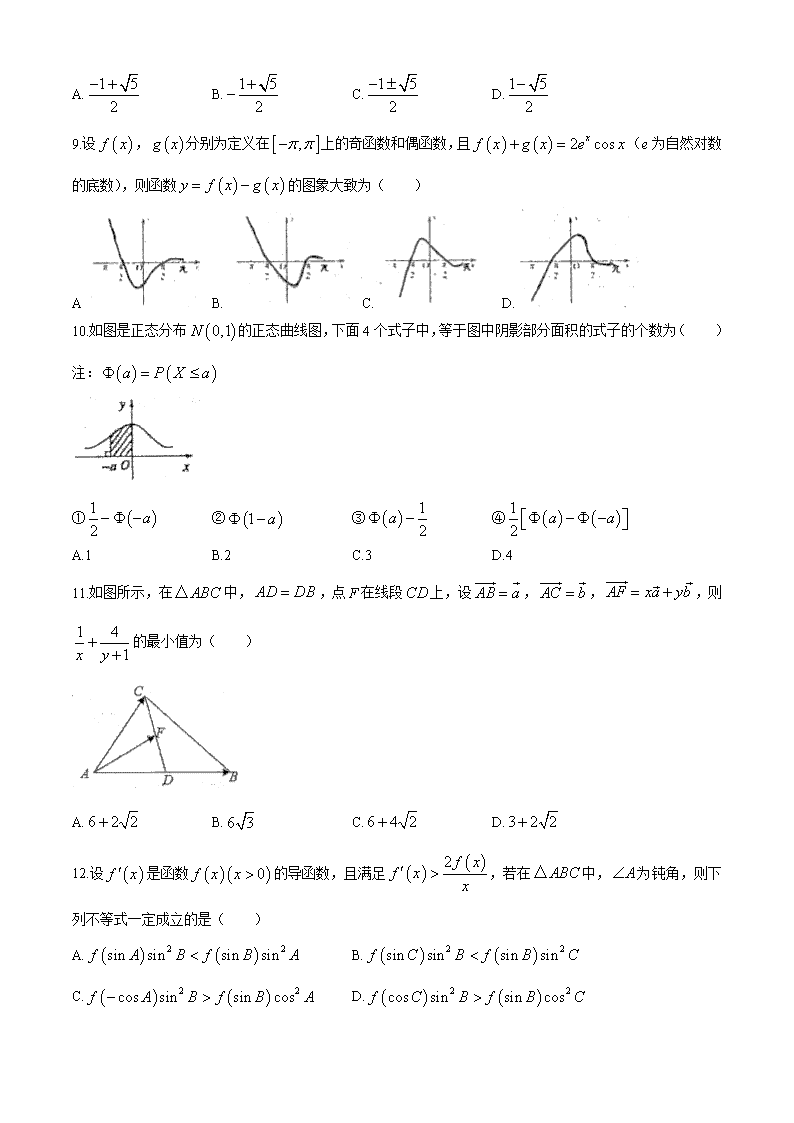
太原五中 2019-2020 学年度第二学期 6 月模拟考试(一) 高三数学(理) 一、选择题:本题共 12 小题,每小题 5 分,共 60 分,每小题只有一个正确选项. 1.已知集合 4 4 0A x x x , 2 24 16B y x y .则 A B ( ) A. 3, 3 B. 2,2 C. 4,4 D. 2.设 z a bi 且 a b R、 ,“z 是纯虚数”是“ 0a ”的( ) A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分也不必要条件 3.若双曲线 2 2 2 1 09 y x aa 的一条渐近线与直线 1 3y x 垂直,则此双曲线的实轴长为( ) A.18 B.9 C.6 D.3 4.已知方程 ln 11 2x x 的根为 0x ,且 0 , 1x k k , *k N ,则 k ( ) A.2 B.3 C.4 D.5 5.已知某线性规划问题的约束条件是 3 4 y x y x x y ,则下列目标函数中,在点 3,1 处取得最小值的是( ) A. 2 z x y B. 2z x y C. 1 2z x y D. 2z x y 6.把 9 个完全相同的口罩分给 6 名同学,每人至少一个,不同的分法有( )种 A.41 B.56 C.156 D.252 7.如图所示,用一边长为 2 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为 4 3 的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( ) A. 2 1 2 B. 2 1 2 C. 6 1 2 D. 3 1 2 8.已知 3, 2 , 2sin 2 1 cos2 ,则 tan 2 ( ) A. 1 5 2 B. 1 5 2 C. 1 5 2 D.1 5 2 9.设 f x , g x 分别为定义在 , 上的奇函数和偶函数,且 2 cosxef x xg x (e 为自然对数 的底数),则函数 y f x g x 的图象大致为( ) A B. C. D. 10.如图是正态分布 0,1N 的正态曲线图,下面 4 个式子中,等于图中阴影部分面积的式子的个数为( ) 注: a P X a ① 1 2 a ② 1 a ③ 1 2a ④ 1 2 a a A.1 B.2 C.3 D.4 11.如图所示,在 ABC△ 中, AD DB ,点 F 在线段CD 上,设 AB a , AC b , AF xa yb ,则 1 4 1x y 的最小值为( ) A. 6 2 2 B. 6 3 C. 6 4 2 D.3 2 2 12.设 f x 是函数 0f x x 的导函数,且满足 2 f xf x x ,若在 ABC△ 中, A 为钝角,则下 列不等式一定成立的是( ) A. 2 2sin sin sin sinf A B f B A B. 2 2sin sin sin sinf C B f B C C. 2 2cos sin sin cosf A B f B A D. 2 2cos sin sin cosf C B f B C 二、填空题:本题共 4 小题,每小题 5 分,共 20 分. 13. 202050 3 被 7 除后的余数为________________________. 14.若顶点在原点的抛物线经过三个点 2,1 , 1,2 , 4,4 中的 2 个点,则满足要求的抛物线的标准方程 有_______________________. 15.如图,在棱长为 2 的正方体 1 1 1 1ABCD A B C D 中, E , F , G 分别是棱 AB , BC , 1CC 的中点,P 是底面 ABCD 内一动点.若直线 1D P 与平面 EFG 不存在公共点,设直线 1D P 与直线 1C C 所成角为 ,则 cos 的取值范围是___________________. 16. ABC△ 中,三个内角 A , B , C 所对的边分别为 a ,b , c .且 2 2 2 2 3sin SA C a c b ,若 AC 边 上的中线 BM 的长为 2,则 ABC△ 面积的最大值为____________________. 三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.17-21 题为必考题,每个试题考生都必须 作答.第 22、23 题为选考题,考生根据要求作答. (一)必考题:共 60 分. 17.(12 分) 如图所示的多面体 ABCDEF 满足:正方形 ABCD 与正三角形 FBC 所在的两个平面互相垂直, //FB EA 且 2FB EA . (1)证明:平面 EFD 平面 ABFE ; (2)求二面角 E FD C 的余弦值. 18.(12 分) 设各项均为正数的数列 na 的前 n 项和为 nS ,已知 1 1a ,且 1 1 1n n n n n na S a S a a ,对一切 *n N 都成立. (1)当 1 时,证明数列 1 n n S a 是常数列,并求数列 na 的通项公式; (2)是否存在实数 ,使数列 na 是等差数列?若存在,求出 的值;若不存在,说明理由. 19.(12 分) 已知椭圆 2 2 2 2: 1 0x yC a ba b 经过点 3,1 ,离心率为 6 3 . (1)求椭圆 C 的方程; (2)过点 4,0M 的直线交椭圆于 A,B 两点,若 AM MB ,在线段 AB 上取点 D,使得 AD DB . 求证:点 D 在定直线上. 20.(12 分) 为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生 产线的技术改造前后各 20 次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图: (1)(Ⅰ)设所采集的 40 个连续正常运行时间的中位数 m,并将连续正常运行时间超过 m 和不超过 m 的 次数填入下面的列联表: 超过 m 不超过 m 改造前 改造后 (Ⅱ)根据(Ⅰ)中的列联表,能否有 99%的把握认为生产线技术改造前后的连续正常运行时间有差异? 附: 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d 2P K k 0.050 0.010 0.001 k 3.841 6.635 10.828 (2)工厂的生产线的运行需要进行维护,工厂对生产线的生产维护费用包括正常维护费、保障维护费两种. 对生产线设定维护周期为 T 天(即从开工运行到第 T 天 *k N 进行维护.生产线在一个生产周期内设置几 个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费; 若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为 0.5 万元/次;保障维护费第一次为 0.2 万元/周期,此后每增加一次则保障维护费增加 0.2 万元.现制定生产线一个生产周期(以 120 天计)内的维 护方案: 30T , 1,2,3,4k 以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的 分布列. 21.(12 分) 已知函数 1x xf x ae 的两个零点记为 1x , 2x . (1)求 a 的取值范围; (2)证明: 1 2 2 1x x a . (二)选考题:共 10 分.请考生在 22、23 题中任选一题做答,如果多做,则按所做第一题记分. 22.(10 分)选修 4-4:坐标系与参数方程 在平面直角坐标系 xOy 中,直线l 的参数方程为 2 3 4 3 x at y t (其中 t 为参数),以坐标原点 O 为极点,x 轴的正半轴为极轴的极坐标系中,点 A 的极坐标为 2, 6 ,直线 l 经过点 A.曲线 C 的极坐标方程为 2sin 4cos . (1)求直线l 的普通方程与曲线 C 的直角坐标方程; (2)过点 3,0P 作直线l 的垂线交曲线 C 于 D,E 两点(D 在 x 轴上方),求 1 1 PD PB 的值. 23.(10 分)选修 4-5:不等式选讲 已知函数 0, 0f x x a x b a b . (1)当 1a b 时,解不等式 2f x x ; (2)若 f x 的值域为 3, ,证明: 2 2 42 81a b b a b . 太原五中 2020 年 6 月数学(理科)答案和解析 一、选择题:1-12 BAAC ABDB ACDD 二、填空题 13.4; 14. 2 4x y 或 2 4y x 15. 2 6,2 3 ; 16.8 4 3 三、解答题 17 解:(1)由题可得,∵四边形 ABCD 是正方形且三角形 FBC 是正三角形,所以 //BC AD , BC AD , FB BC 且 60FBC , 又∵ //EA FE , 2EA FB ,所以 60EAD ,在三角形 EAD 中,根据余弦定理可得: ED AE . ∵平面 ABCD 平面 FBC , AB BC ,平面 ABCD 平面 FBC BC ,且 AB 平面 ABCD ,所以 AB 平面 BCF , ∵ //BC A, //EA FB ,FB BC B ,且 FB BC 、 平面 FCB , ,EA AD 平面 EAD ,所以平面 //EAD 平面 FBC ,所以 AB 平面 EAD , 又∵ ED 平面 EAD ,所以 AB ED , 综上: ED AE , ED AB , EA AB A 且 ,EA AB 面 ABFE ,所以 DE 平面 ABFE , 又∵ DE 平面 DEF ,所以平面 EFD 平面 ABFE . (2)如图,分别取 BC 和 AD 的中点 O,G,连接OF ,OG , 因为 BO OC 且三角形 FBC 为正三角形,所以 FO BC , 因为 AG GD , BO OC ,所以 //OG AE , 由(1)可得, AB 平面 FBC ,则OG 平面 FBC , 故OF 、OB 、OG 两两垂直,分别以OB 、OG 、OF 所在直线为 x,y,z 轴建立如图所示的空间直角坐 标系, 不设 4BC ,则 0,0,2 3F , 2,0,0C , 2, 4,0D , 1, 4, 3E 设平面 DEF 的法向量为 1 1 1, ,n x y z ,平面 DCF 的法向量为 2 2 2, ,m x y z , 则 1 1 1 1 1 2 4 2 3 00 1,1, 3 0 3 3 0 x y zDF n n DE n x z , 则 2 2 2 2 0 2 4 2 3 0 3,0, 1 4 00 DF m x y z m yDC m , 所以 6 15cos , 52 15 n n m mn m 又二面角 E FD C 是钝二面角,所以二面角 E FD C 的余弦值为 15 5 . 18.解:(1)①当 1 时, 1 1 1n n n n n na S a S a a , 则 1 1 1n n n n nna S aa S a , 即 1 11 1n n n nS a S a . ∵数列 na 的各项均为正数, ∴ 1 1 1 1 n n n n Sa Sa . ∴ 3 1 3 12 2 1 2 1 2 1 11 1 1 1 n n n n a a S Sa S a a a S S S , 化简,得 1 11 2n nS a ,① ∴当 2n 时, 1 2n nS a ,② ②-①,得 1 2n na a , ∵当 1n 时, 2 2a ,∴ 1n 时上式也成立, ∴数列 na 是首项为 1,公比为 2 的等比数列,即 12n na . (2)由题意,令 1n ,得 2 1a ;令 2n ,得 2 3 1a . 要使数列 na 是等差数列,必须有 2 1 32a a a ,解得 0 . 当 0 时, 1 11n n n nS a S a ,且 2 1 1a a . 当 2n 时, 1 1 11n n n n n nS S S S S S , 整理,得 2 1 1 1n n n n nS S S S S ,即 1 1 1 1 n n n n S S S S , 从而 3 3 12 4 1 2 1 2 3 1 11 1 1 1 n n n n S S S SS S S S S S S S , 化简,得 11n nS S ,即 1 1na . 综上所述,可得 1na , *n N . ∴ 0 时,数列 na 是等差数列. 19.解:(1)由题意得 2 2 6 3 3 1 1 c a a b ,解得 6a , 2b , 2c , 所以椭圆 C 的方程为 2 2 16 2 x y . (2)证明:设直线 AB 的方程为 4x my , 1 1,A x y , 2 2,B x y , 0 0,D x y , 由 2 2 4 16 2 x my x y ,得 2 23 8 10 0m y my , 2 28 40 3 0n m ,则 2 5m , 则有 1 2 2 8 3 my y m , 1 2 2 10 3y y m , 由 AM MB ,得 1 2y y , 由 AD DB 可得 1 2 0 1 2 0 1 1 x xx y yy , 1 21 2 0 4 4 1 1 my myx xx 2 1 1 2 1 2 1 2 2 1022 2 334 4 48 21 3 mmy my y m y my y my , 2 1 2 1 1 2 0 1 2 1 2 2 1022 2 53 81 21 3 y y y y y my y my y m my . 综上,点 D 在定直线 3 2x 上. 20.解:(Ⅰ)(1)由茎叶图的数据可得中位数 29 31 302m , 根据茎叶图可得: 5a , 15b , 15c , 5d , 超过 m 不超过 m 改造前 5 15 改造后 15 5 (2)根据(1)中的列联表, 2 2 2 ( ) 40(5 5 15 15) 10 6.636( )( )( )( ) 20 20 20 20 n ad bcK a b c d a c b d , 有 99%的把握认为生产线技术改造前后的连续正常运行时间有差异; (Ⅱ)120 天的一个生产周期内有 4 个维护周期,一个维护周期为 30 天,一个维护周期内,以生产线在技 术改造后一个维护周期内能连续正常运行的频率作为概率,得 5 1 20 4p , 设一个生产周期内需要 次维护, 1~ 4, 4B ,正常维护费为 0.5 4 2 万元, 保 障 维 护 费 为 首 项 为 0.2 , 公 差 为 0.2 的 等 差 数 列 , 共 次 维 护 需 要 的 保 障 费 为 20.2 0.2 1 0.2 0.1 0.12 元, 故一个生产周期内保障维护 X 次的生产维护费为 20.1 0.1 2 万元, 设一个生产周期内的生产维护费为 X 万元,则 X 可能取值为 2,2.2,2.6,3.2,4, 则 4 0 4 3 812 4 256P X C , 3 1 4 1 3 272.2 4 4 64P X C , 2 2 2 4 1 3 272.6 4 4 128P X C , 3 3 4 1 3 33.2 4 4 64P X C , 41 14 4 256P X , 则 X 的分布列为: X 2 2.2 2.6 3.2 4 P 81 256 27 64 27 128 3 64 1 256 21.解:(Ⅰ)由 0f x 得 1x xa e , 令 1xg x x e , 1 1 xg x x e , 当 1x , 0g x , g x 递增, 当 1x , 0g x , g x 递减, 因为当 0x , 0g x ;当 0x , 0g x ,且 0 0g , 1 1g , 0x , 0g x , x , 0g x , 所以函数有两个不同的零点,此时 0 1a ; (Ⅱ)先证 1 2 2x x , 不妨设 1 2x x ,由(1)可知, 1 20 1x x , 构造函数 1 12 2x xF x f x f x xe x e , 1 11 x xF x x e e , 当 0 1x , 0F x , F x 递增, 1 0F , 0F x , 所以 1 0F x ,即 1 12f x f x 因为 1 20 1x x ,所以 12 1x , 1 2f x f x , 由(1)可知 f x 在 1, 是递增, 2 12x x ,即 1 2 2x x , 要证明 1 2 2 1x x a ,只需证明 2 1 11 1 2 1 2 1x x x a , 即 2 1 12x x a , 1 1 1x xa e , 只需证明 1 21 1 11 2 0x x x xe , 10 1x , 令 2 1 2x xh x x xe , 1 11 2xh x x e , 当 0,1 ln 2x , 0h x , h x 递增, 当 1 ln 2,1x , 0h x , h x 递减, 当 0 1x , min min 0 , 1 0h x h h , 0h x ,故 1 2 2 1x x a . 22.解:(1)由题意得点 A 的直角坐标为 3,1 ,将点 A 代入 2 3 4 3 x at y t 得 1 3 a t , 则直线l 的普通方程为 3 2y x . 由 2sin 4cos 得 2 2sin 4 cos ,即 2 4y x . 故曲线 C 的直角坐标方程为 2 4y x . (2)设直线 DE 的参数方程为 33 2 1 2 x t y t (t 为参数), 代入 2 4y x 得 2 8 3 16 3 0t t . 设 D 对应参数为 1t , E 对应参数为 2t . 则 1 2 8 3t t , 1 2 16 3t t ,且 1 0t , 2 0t . ∴ 1 2 1 2 1 2 1 2 1 1 1 1 1 1 1 2 t t PD PE t t t t t t . 23.解:(Ⅰ)当 1a b 时,不等式为 1 1 2x x x , 当 1x 时,不等式化为 22 2 3x x x ,此时不等式无解; 当 1 1x 时,不等式化为 2 2 0x x ,故 0 1x ; 当 1x 时,不等式化为 2 2 2x x x ,故1 2x . 综上可知,不等式的解集为 0 2x x . (Ⅱ) f x x a x b a b ,当且仅当 x a 与 x b 同号时, f x 取得最小值 a b , ∵ f x 的值域为 3, ,且 0a , 0b ,故 3a b . 故 22 2 22 1 1a b b a b , 22 1 1 22 2 a b a b , ∴ 22 1 8a b ( 当 且 仅 当 1 2a b 时取等号). 又∵ 1 2 1a b a b ,∴ 41a b ,∴ 4 11a b ,(等号成立条件同上) ∴ 2 2 42 81a b b a b .查看更多