【数学】2018届一轮复习人教A版函数的单调性与最值教案
1.理解函数的单调性、最大值、最小值及其几何意义.
2.会运用基本初等函数的图象分析函数的性质.
知识点一 函数的单调性
1.单调函数的定义
增函数
减函数
定义
一般地,设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量x1,x2
当x1
f(x2)
2.增函数 减函数 区间D
1.(2016·北京卷)下列函数中,在区间(-1,1)上为减函数的是( )
A.y= B.y=cosx
C.y=ln(x+1) D.y=2-x
解析:函数y=,y=ln(x+1)在(-1,1)上都是增函数,函数y=cosx在(-1,0)上是增函数,在(0,1)上是减函数,而函数y=2-x=()x在(-1,1)上是减函数,故选D.
答案:D
2.(必修①P39A组第3题改编)函数y=(2m-1)x+b在R上是减函数,则( )
A.m> B.m<
C.m>- D.m<-
解析:若y=(2m-1)x+b在R上是减函数,则2m-1<0,即m<.
答案:B
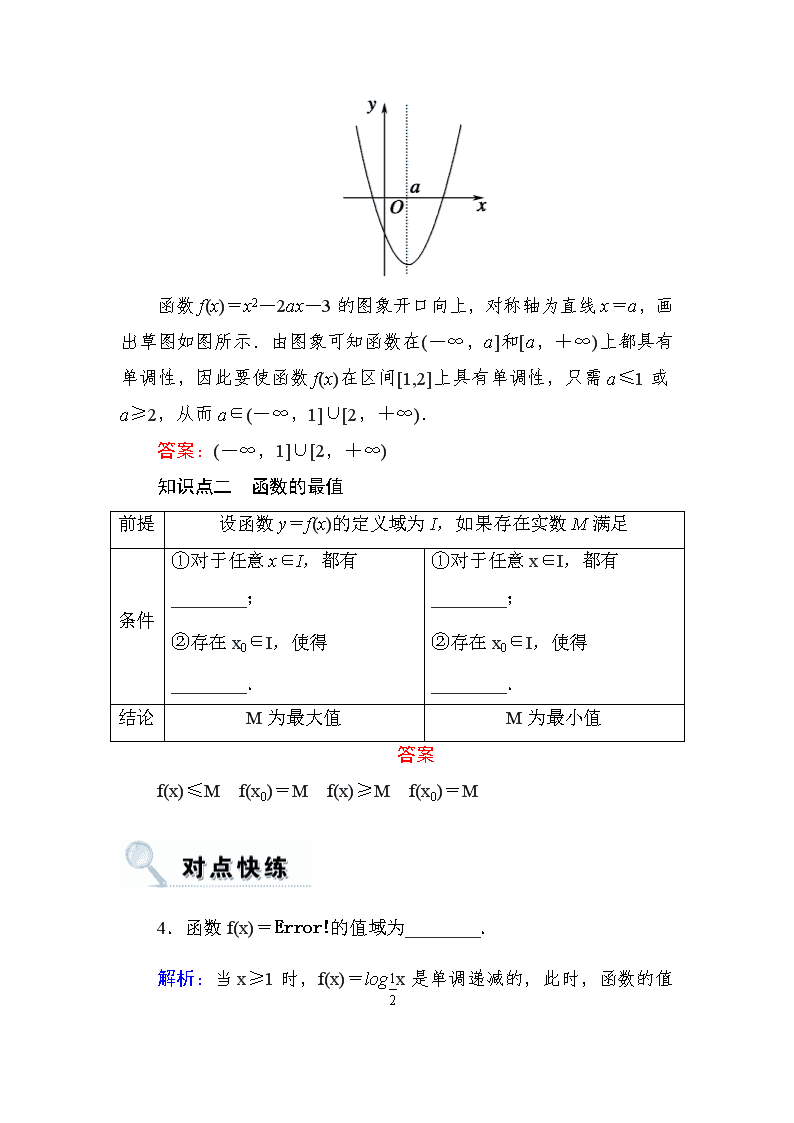
3.已知函数f(x)=x2-2ax-3在区间[1,2]上具有单调性,则实数a的取值范围为________.
解析:
函数f(x)=x2-2ax-3的图象开口向上,对称轴为直线x=a,画出草图如图所示.由图象可知函数在(-∞,a]和[a,+∞)上都具有单调性,因此要使函数f(x)在区间[1,2]上具有单调性,只需a≤1或a≥2,从而a∈(-∞,1]∪[2,+∞).
答案:(-∞,1]∪[2,+∞)
知识点二 函数的最值
前提
设函数y=f(x)的定义域为I,如果存在实数M满足
条件
①对于任意x∈I,都有
________;
②存在x0∈I,使得________.
①对于任意x∈I,都有
________;
②存在x0∈I,使得________.
结论
M为最大值
M为最小值
答案
f(x)≤M f(x0)=M f(x)≥M f(x0)=M
4.函数f(x)=的值域为________.
解析:当x≥1时,f(x)=log
x是单调递减的,此时,函数的值域为(-∞,0];x<1时,f(x)=2x是单调递增的,此时,函数的值域为(0,2).综上,f(x)的值域是(-∞,2).
答案:(-∞,2)
5.(必修①P31例4改编)函数f(x)=在[2,6]上的最大值和最小值分别是________.
解析:函数f(x)===2+在[2,6]上单调递减,所以f(x)min=f(6)==.
f(x)max=f(2)==4.
答案:4,
热点一 函数单调性的判断与证明
【例1】 (1)下列四个函数中,在(0,+∞)上为增函数的是( )
A.f(x)=3-x B.f(x)=x2-3x
C.f(x)=- D.f(x)=-|x|
(2)试讨论函数f(x)=(a≠0)在(-1,1)上的单调性.
【解析】 (1)当x>0时,f(x)=3-x为减函数;当x∈时,f(x)=x2-3x为减函数;当x∈时,f(x)=x2-3x为增函数;当x∈(0,+∞)时,f(x)=-为增函数;当x∈(0,+∞
)时,f(x)=-|x|为减函数.
(2)解:设-10,x1-1<0,x2-1<0,
故当a>0时,f(x1)-f(x2)>0,即f(x1)>f(x2),函数f(x)在(-1,1)上递减;
当a<0时,f(x1)-f(x2)<0,即f(x1)0时,f(x)在(-1,1)上单调递减;当a<0时,f(x)在(-1,1)上单调递增.
【答案】 (1)C
【总结反思】
确定函数单调性的方法:(1)定义法和导数法,证明函数单调性只能用定义法和导数法;(2)复合函数法,复合函数单调性的规律是“同增异减”;(3)图象法,图象不连续的单调区间不能用“∪”连接.
已知a>0,函数f(x)=x+(x>0),证明:函数f(x)在(0,]上是减函数,在[,+∞)上是增函数.
证明:方法1:任意取x1>x2>0,则f(x1)-f(x2)=-
=(x1-x2)+
=(x1-x2)+
=(x1-x2).当≥x1>x2>0时,x1-x2>0,1-<0,有f(x1)-f(x2)<0,即f(x1)0)在(0,]上为减函数;
当x1>x2≥时,x1-x2>0,1->0,有f(x1)-f(x2)>0,即f(x1)>f(x2),
此时,函数f(x)=x+(a>0)在[,+∞)上为增函数;
综上可知,函数f(x)=x+(a>0)在(0,]上为减函数,在[,+∞)上为增函数.
方法2:f′(x)=1-,令f′(x)>0,则1->0,解得x>或x<-(舍).令f′(x)<0,则1-<0,解得-0,∴00,则x<1或x>2.
∴函数y=log (x2-3x+2)的定义域为(-∞,1)∪(2,+∞).又u=x2-3x+2的对称轴x=,且开口向上.
∴u=x2-3x+2在(-∞,1)上是单调减函数,在(2,+∞)上是单调增函数.
而y=logu在(0,+∞)上是单调减函数,
∴y=log (x2-3x+2)的单调递减区间为(2,+∞),单调递增区间为(-∞,1).
【总结反思】
求函数的单调区间与确定单调性的方法一致
(1)利用已知函数的单调性,即转化为已知函数的和、差或复合函数,求单调区间.
(2)定义法:先求定义域,再利用单调性定义.
(3)图象法:如果f(x)是以图象形式给出的,或者f(x)的图象易作出,可由图象的直观性写出它的单调区间.
(4)导数法:利用导数取值的正负确定函数的单调区间.
求下列函数的单调区间:
(1)y=x2-x;
(2)y=3x2-6lnx.
解:(1)设u=x2-x,则y=u.
∵u在上为减函数,
在上为增函数,又∵y=u为减函数,
∴y=x2-x在上为增函数,在上为减函数.
(2)y′=6x-=.
∵定义域为(0,+∞),
由y′>0,得x>1,∴增区间为(1,+∞).
由y′<0,得00
C.f(x1)>0,f(x2)<0
D.f(x1)>0,f(x2)>0
【解析】 因为f(x)在(1,+∞)上是增函数,且f(2)=log22+=0,又x1∈(1,2),所以f(x1)f(2)=0.
【答案】 B
考向2 解不等式
【例4】 已知偶函数f(x)在[0,+∞)上单调递减,f(2)=0.若f(x-1)>0,则x的取值范围是________.
【解析】
由题意,得函数f(x)的草图如图所示.
因为f(x-1)>0,所以|x-1|<2,
所以-2x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,设a=f,b=f(2),c=f(e),则a,b,c的大小关系为( )
A.c>a>b B.c>b>a
C.a>c>b D.b>a>c
(2)f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞) B.(8,9]
C.[8,9] D.(0,8)
(3)已知函数f(x)=若f(x)在(-∞,+∞)上单调递增,则实数a的取值范围为________.
解析:(1)因f(x)的图象关于直线x=1对称.由此可得f=f.由x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,知f(x)在(1,+∞)上单调递减.
∵1<2<f>f(e).∴b>a>c.
(2)2=1+1=f(3)+f(3)=f(9),由f(x)+f(x-8)≤2,可得f[x(x-8)]≤f(9),因为f(x)是定义在(0,+∞)上的增函数,所以有解得80,∴f(x)在[1,2]上为增函数,
又f(1)=5,f(2)=7.∴f(x)=3x+,x∈[1,2]的值域为[5,7].
答案:(1)(-∞,3) (2)[5,7]
1.单调区间是定义域的子区间,求单调区间定义域优先.
2.熟记各基本初等函数的单调区间,是求单调区间的前提、基础.
3.对于对勾函数y=x+(a>0),单调递增区间:(-∞,-],[,+∞);单调递减区间:[-,0),(0,].
4.函数的单调增、减区间要分开写;两个(或两个以上)同一类单调区间之间用“,”隔开,不能用“∪”符号连接.
5.若f(x)具有对称轴x=a,则在x=a两侧的对称区间上f(x)具有相反的单调性.
若f(x)具有对称中心(a,b),则在x=a两侧的对称区间上f(x)具有相同的单调性.
6.函数图象的平移不影响单调性;其中左右平移能改变单调区间,上下平移不改变单调区间.
抽象函数的几个解题技巧
抽象函数是指没有明确给出具体的函数表达式,只是给出了一些体现函数特征的式子的一类函数,如函数的定义域,解析递推式,特定点的函数值,特定的运算性质等.它是中学数学中的一个难点,抽象性较强,灵活性大,解决抽象函数问题最重要的一点是要抓住函数中的某些性质,利用数学方法(如赋值法、化归法、数形结合法等),这样就能突破“抽象”带来的困难,做到胸有成竹.另外还要通过对题目的特征进行观察、分析、类比和联想,寻找具体的函数模型,再由具体函数模型的图象和性质来指导我们解决抽象函数问题.本文对这一问题进行了初步整理、归类,大概有以下几种题型:
一、利用赋值法求抽象函数的值
【例1】 定义在R上的函数f(x)满足:f(x)=f(4-x)且f(2-x)+f(x-2)=0,则f(2 016)的值为________.
【解析】 由f(2-x)+f(x-2)=0,令t=x-2,代入,有f(-t)=-f(t),∴f(x)为奇函数且有f(0)=0,又f(x+4)=f[4-(x+4)]=f(-x)=-f(x),∴f(x+8)=-f(x+4)=f(x),故f(x)是周期为8的周期函数,∴f(2 016)=f(0)=0.
【答案】 0
解题策略:这类抽象函数一般是给出定义域,某些性质及运算式来求特殊值.其解法常用“特殊值法”,即在其定义域内令变量取某特殊值而获解,关键是使抽象问题具体化.
二、利用配凑法证明抽象函数的单调性
【例2】 已知函数f(x)对任意x,y∈R有f(x)+f(y)=2+f(x+y),当x>0时,f(x)>2,f(3)=5.求不等式f(a2-2a-2)<3的解集.
【解】 设x1,x2∈R且x10,∴f(x2-x1)>2,即f(x2-x1)-2>0,∴f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-2>f(x1),∴f(x2)>f(x1),故f(x)为增函数,又f(3)=f(2+1)=f(2)+f(1)-2=3f(1)-4=5,∴f(1)=3,∴f(a2-2a-2)<3=f(1),即a2-2a-2<1,∴-1
查看更多